Newton's iteration method 是在实数域和复数域利用切线不断逼近方程根的一种求高次曲线方程的方法，区别于梯度下降法，它是二阶导，收敛速度比较快，对于非凸函数，牛顿法容易受到鞍点或者最大值点的吸引。由于牛顿迭代法是局部收敛，初始值选取不当的话，很容易无法收敛。

目录

1 基本介绍

2 公式推导

3 牛顿迭代法的应用

3.1 求倒数

3.2 开根号

 3.2 马克尔的方法

4 收敛性分析

---

1 基本介绍

        牛顿迭代法（Newton's method）又称为牛顿-拉夫逊（拉弗森）方法（Newton-Raphson method），它是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方法。

牛顿迭代法实质是一种求根算法，这意味着它的目标是找到函数 f(x)=0 的值 x。在几何上可以将其视为 x 的值，这时函数与 x 轴相交。

2 公式推导

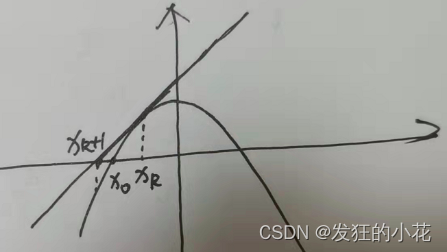
 对于 求解此时方程的根，任取近似作为方程的根，利用切线逼近法，可知对于在点做切线与轴的交点的横坐标一定更加逼近。

由此可以得到  ，

化简后得到此时的近似值  ，这就是牛顿迭代法的公式

3 牛顿迭代法的应用

3.1 求倒数

        有些芯片设计的对于求倒数的方法就是使用的牛顿迭代法，对于求解的倒数，有公式，对于牛顿迭代法设置初值，那么就是已知数，是自变量，由此得到，求解的根，带入到牛顿迭代法公式中得到 ，这就是求导数的牛顿迭代法公式，在ARM Neon中有专门的Intrinsic 指令 float32x4_t   = vmulq_f32(vrecpsq_f32(a, ), )来并行求倒数；由于计算机中的直接求倒数一般精度不够或者运行效率比较低，因此可以使用牛顿迭代法来求，在卷积计算中，经常会遇到除法运算，实质上就是求倒数。

3.2 开根号

        对于开根号某些芯片也是利用牛顿迭代法，对开根号得到，有公式，对于牛顿迭代法设置初值，那么就是已知数，是自变量，由此得到，求解的根，带入到牛顿迭代法公式中得到 ，这就是牛顿迭代法开根号的公式。

3.1 直接的实现

        一般会要求算出的精度，满足精度的情况下就停止运算。代码如下：

double sqrt(double x) { 
	if(x == 0) return 0; 
	double result = x; 
	double lastValue = 0;
	while(fabs(result - lastValue) > EPS) 
	{ 
		lastValue = result; 
		result = result / 2.0f + x / 2.0f / result; 
	}
 	return (double)result;
 }

 3.2 马克尔的方法

        据说非常高效，比3.1的代码快几十倍，比C++标准库函数sqrt快几倍

int sqrt(float x) { 
	if(x == 0) return 0; 
	float result = x; 
	float xhalf = 0.5f*result; 
	int i = *(int*)&result; 
	i = 0x5f375a86- (i>>1); // what the fuck? 
	result = *(float*)&i; 
	result = result*(1.5f-xhalf*result*result); // Newton step, repeating increases accuracy 
	result = result*(1.5f-xhalf*result*result); 
	return 1.0f/result; 
}

4 收敛性分析

        参考牛顿法及其收敛性分析