15. 三数之和

原题链接

题干：

存在一个三元组,满足
i != j、i != k 且 j != k
nums[i] + nums[j] + nums[k] == 0

算法原理：

1、排序 + 暴力枚举 + 利用set 去重

这个方法就是先循环，用几个 for 循环暴力枚举，然后放到 HashSet 中去重
但是这个方法时间复杂度很高，达到了O(N3)

2、排序 + 双指针

（1）排序
这里进行排序是为了从前向后遍历的时候，可以更好的用双指针进行操作

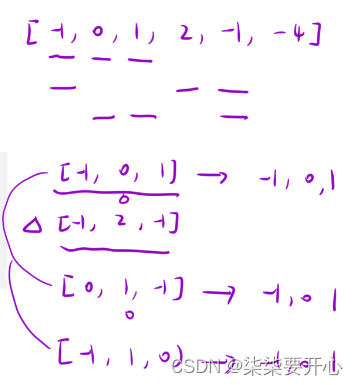
（2）固定一个数 a
这个 a 必须要大于等于 0，因为题目要求三数相加等于 0

（3）在该数后面的区间内，利用“双指针算法”快速找到两个数的和等于 -a 即可

（4）处理细节问题

• 不要漏任何一个组合
  在 left 和 right 向中间走的时候，找到一个数等于固定的数的负数，不能停下，继续缩小区间，寻找下一个

• 去重
  由于题目要求，不能返回相同的数组，所以要求去重
  这样就可以找到一种结果之后，left 和 right 指针要跳过重复元素
  当使用完一次双指正算法之后，也要跳过重复元素
  但要注意避免越界！！！
  

代码：

   public List<List<Integer>> threeSum(int[] nums) {
        List<List<Integer>> ret = new ArrayList<>();

        //1.排序
        Arrays.sort(nums);
        int n = nums.length;

        //2.利用双指针
        for (int i = 0; i < n;) {
            int left = i + 1;
            int right = n - 1;
            int target = -nums[i];
            if (nums[i] > 0) {
                break;
            }
            while (left < right) {
                int sum = nums[left] + nums[right];
                if (sum < target) {
                    left++;
                }else if (sum > target) {
                    right--;
                }else {
                    ret.add(new ArrayList<Integer>(Arrays.asList(nums[i],nums[left],nums[right])));
                    //缩小区间继续寻找
                    left++;
                    right--;
                    while (left < right && nums[left] == nums[left-1]) {
                        left++;
                    }
                    while (left < right && nums[right] == nums[right+1]) {
                        right--;
                    }
                }
            }
            i++;
            while (i < n && nums[i] == nums[i-1]) {
                i++;
            }
        }
        return ret;
    }

18. 18. 四数之和

题干：

这道题跟上面的三数之和非常相似，因此下面的解题思路也是非常相似

nums[a] + nums[b] + nums[c] + nums[d] == target

算法原理：

1、排序 + 暴力枚举 + 利用set 去重

这个算法依然是超时的，我们主要看第二种

2、排序 + 双指针

（1）排序

（2）在 a 后面的区间内，利用“三数之和”找到三个数（和上面题的方法一样），使这三个数的和等于 target - a

（3）处理细节问题

• 不漏
• 去重

代码：

public List<List<Integer>> fourSum(int[] nums, int target) {
        List<List<Integer>> ret = new ArrayList<>();
        int n = nums.length;
        //1.排序
        Arrays.sort(nums);
        //2.双指针
        for (int i = 0; i < n;) {
            long t1 = (long)target - nums[i];
            for (int j = i + 1; j < n;) {
                long t2 = t1 - nums[j];
                int left = j + 1;
                int right = n - 1;
                while (left < right) {
                    int sum = nums[left] + nums[right];
                    if (sum > t2) {
                        right--;
                    }else if (sum < t2) {
                        left++;
                    }else {
                        ret.add(Arrays.asList(nums[i],nums[j],nums[left],nums[right]));
                        left++;
                        right--;
                        while (left < right && nums[left] == nums[left-1]) {
                            left++;
                        }
                        while (left < right && nums[right] == nums[right+1]) {
                            right--;
                        }
                    }
                 }
                j++;
                while (j < n && nums[j] == nums[j-1]) {
                    j++;
                }
            }
            i++;
            while (i < n && nums[i] == nums[i-1]) {
                i++;
            }
        }
        return ret;
    }