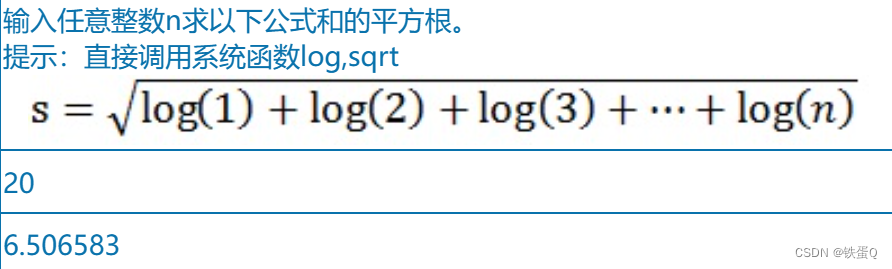
1. 输入任意整数n求以下公式和的平方根。

2. 读取一系列的整数  X，对于每个  X，输出一个  1,2,…,X  的序列。

3. 编写double  fun(int  a[M][M])函数，返回二维数组周边元素的平均值，M为定义好的符号常量。

4. 编写double  fun(int  a[M])函数，返回数组a中所有元素的平均值，并将数组中所有大于平均值的元素按原次序移至数组前部，所有小于等于平均值元素移至数组后部，M为定义好的符号常量。

5. 编写fun函数，求两整数的最大公约和最小公倍数。

#include<stdio.h>
#include<math.h>
int main() {
	int n,i;
	double s = 0;
	scanf("%d", &n);
	for (i = 1; i <= n; i++) {
		s += log(i);
	}
	printf("%lf", sqrt(s));
	return 0;
}

 读取一系列的整数  X，对于每个  X，输出一个  1,2,…,X  的序列。

题干	读取一系列的整数  X，对于每个  X，输出一个  1,2,…,X  的序列。 对于最后一行的整数  0，不作任何处理。
输入样例	5 7 3 0
输出样例	1,2,3,4,5 1,2,3,4,5,6,7 1,2,3

#include<stdio.h>
#include<math.h>
int main() {
	int n, i;
	while (scanf("%d", &n), n) {
		printf("1");
		for (i = 2; i <= n; i++) {
			printf(",%d", i);
		}
		printf("\n");
	}
	return 0;
}

 编写double  fun(int  a[M][M])函数，返回二维数组周边元素的平均值，M为定义好的符号常量。

题干	编写double  fun(int  a[M][M])函数，返回二维数组周边元素的平均值，M为定义好的符号常量。 若M为3，a数组为 1  2  6 4  5  6 7  8  9 调用函数返回5.375

//只填写要求的函数
//#define M 3
double  fun(int  a[M][M]) {
	double s = 0;
	int i, j;
	for (i = 0; i < M; i++) {
		for (j = 0; j < M; j++) {
			if (i == 0 || j == 0 || i == M - 1 || j == M - 1) {
				s += a[i][j];
			}
		}
	}
	return s / (4 * M - 4);
}

 编写double  fun(int  a[M])函数，返回数组a中所有元素的平均值，并将数组中所有大于平均值的元素按原次序移至数组前部，所有小于等于平均值元素移至数组后部，M为定义好的符号常量。

题干	编写double  fun(int  a[M])函数，返回数组a中所有元素的平均值，并将数组中所有大于平均值的元素按原次序移至数组前部，所有小于等于平均值元素移至数组后部，M为定义好的符号常量。 若M为8，a原数组为[2,1,5,7,4,9,3,6] 调用函数后返回4.625000，a数组变为[5,7,9,6,2,1,4,3]

//只填写要求的函数
double  fun(int  a[M]) {
	int i = 0,average,b[M],c[M],bi=0,ci=0;
	double s = 0;
	for (i = 0; i < M; i++) {
		s += a[i];
	}
	average = s / M;
	for (i = 0; i < M; i++) {
		if (a[i] > average) {
			b[bi++] = a[i];
		}
		else {
			c[ci++] = a[i];
		}
	}
	i--,bi--,ci--;
	while (ci >= 0) {
		a[i--] = c[ci--];
	}
	while (bi >= 0) {
		a[i--] = b[bi--];
	}
	return s / M;
}

 编写fun函数，求两整数的最大公约和最小公倍数。

题干	编写fun函数，求两整数的最大公约和最小公倍数。 void  main() {         int  a,b,gy,gb;         scanf("%d%d",&a,&b);         fun(a,b,&gy,&gb);         printf("%d  %d\n",gy,gb); }

//只填写要求的函数
void fun(int a, int b, int* gy, int* gb) {
	int i=a<b?a:b;
	for (i; i > 0; i--) {
		if (a % i == 0 && b % i == 0) {
			break;
		}
	}
	*gy = i;
	*gb = (a * b) / i;
}