定义

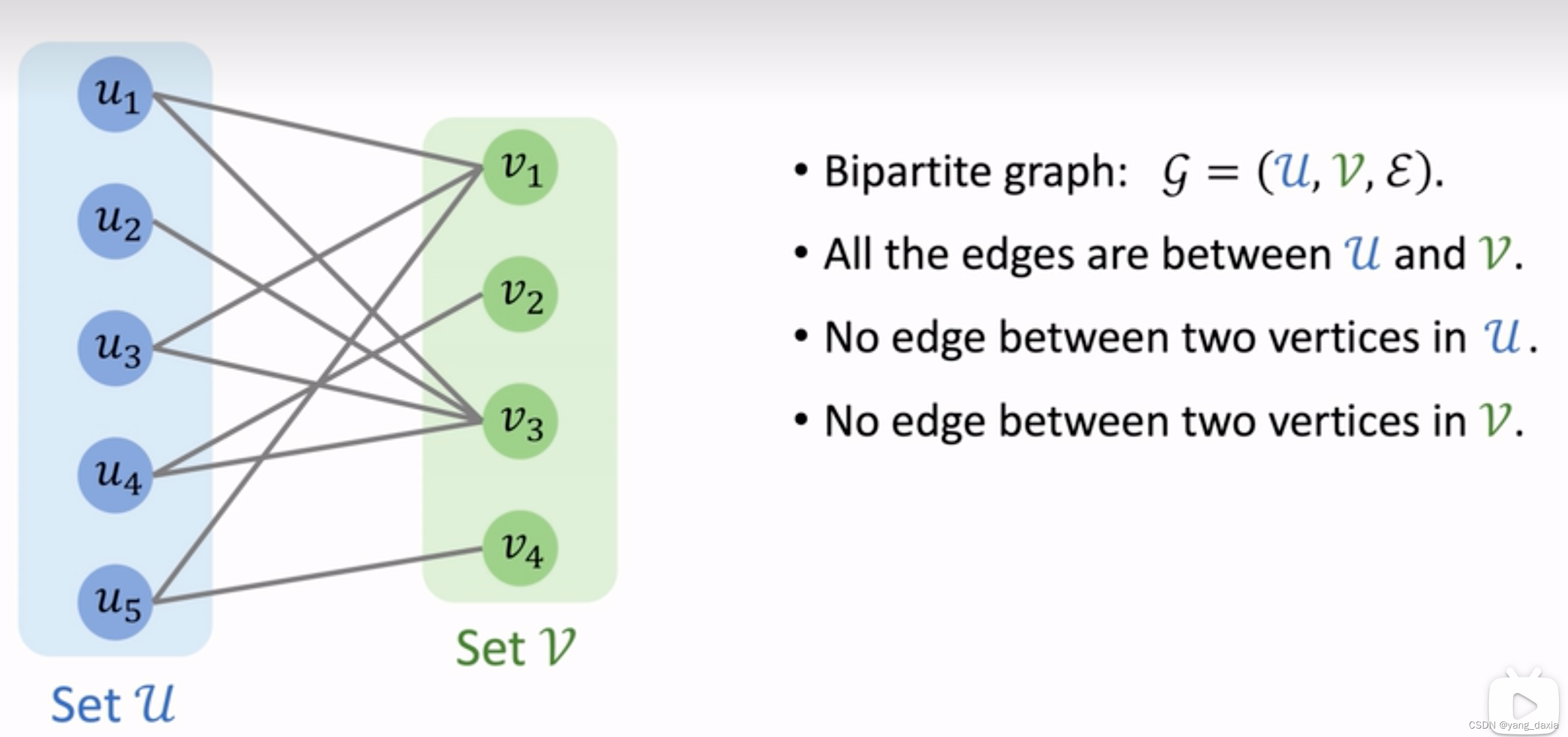
• 节点u直接无边，v之间无边，边只存在uv之间。
• 判断方法：BFS染色法，全部染色后，相邻边不同色

无权二部图中的最大匹配

• 最大匹配即每一个都匹配上min（u， v）。
• 贪心算法可能导致，有些节点未匹配上
• 可以添加起始节点以及终止节点，使用网络流算法进行求解。

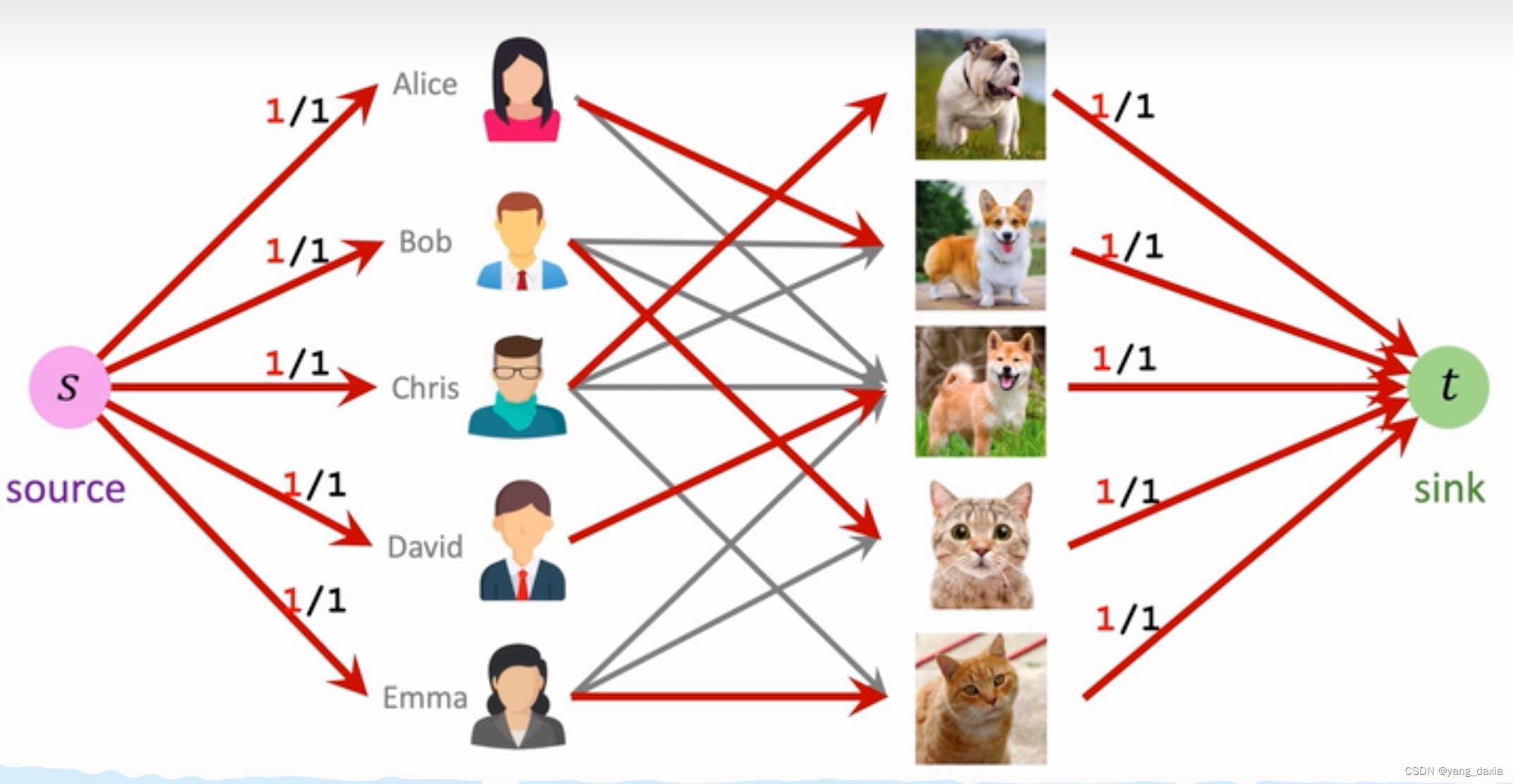
有权二部图中的最大匹配Maximum-Weight Bipartite Matching

• 每一条边都有权重，最大匹配追求的是整体的权重和最大。（整体收益最大）
• 最大匹配可以转化为最小匹配算法。即把权重*-1, 最小匹配的结果就是最大匹配的结果。
• 匈牙利算法可以解决最小匹配问题，但是u和v的节点数量需要保持一致，算法复杂度为O(n^3),暴力为O(n!)

匈牙利算法

• 构建u*u矩阵，没有边的为0

• 每一行减去每一行的最小值
  

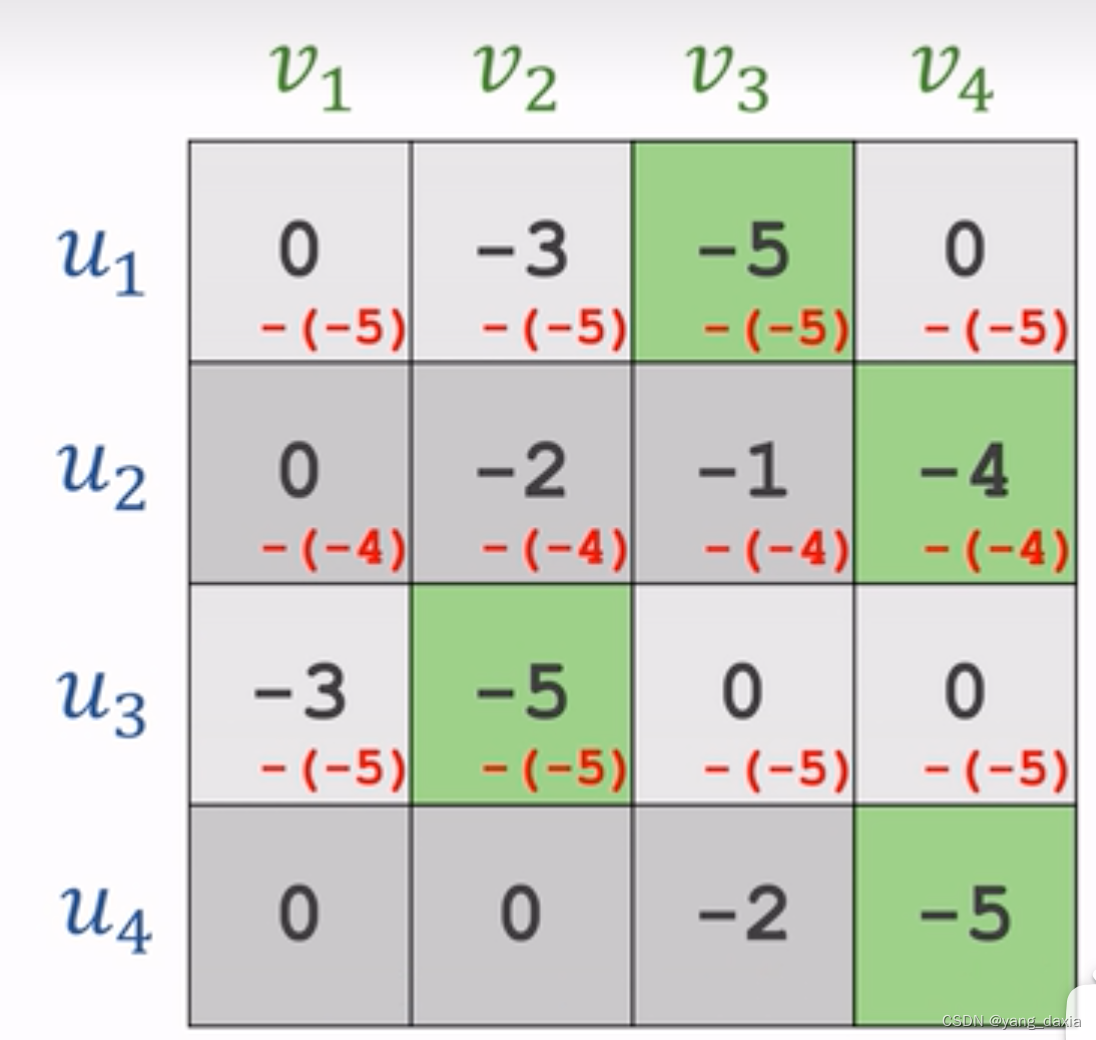
• 每一列减去每一列的最小值
  

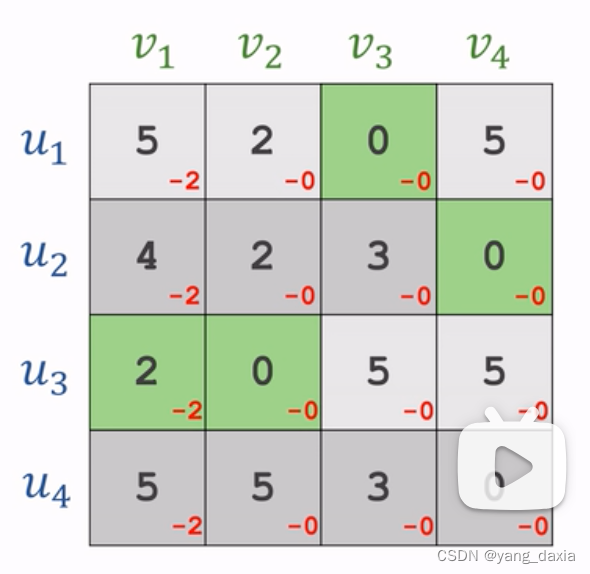
• 使用最小的线覆盖所有的0。如果线的数量小于u的数量，则剩下的继续找最小元素，然后递减，节点处加上该元素；如果数量相同，则优先找唯一有0的点进行匹配。
  
  
  
  

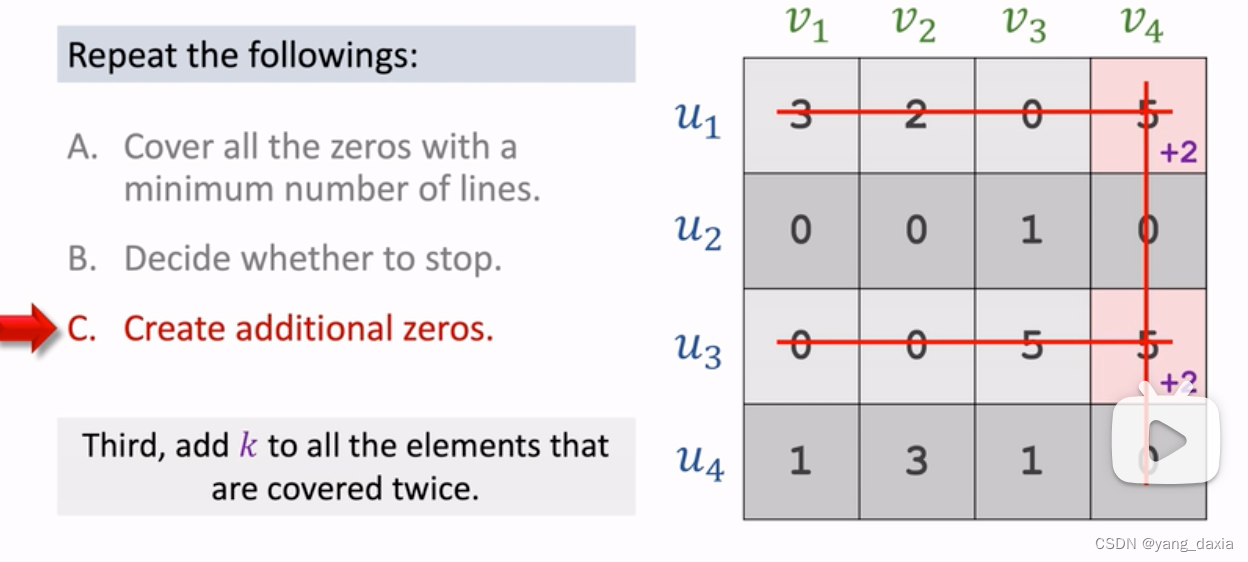
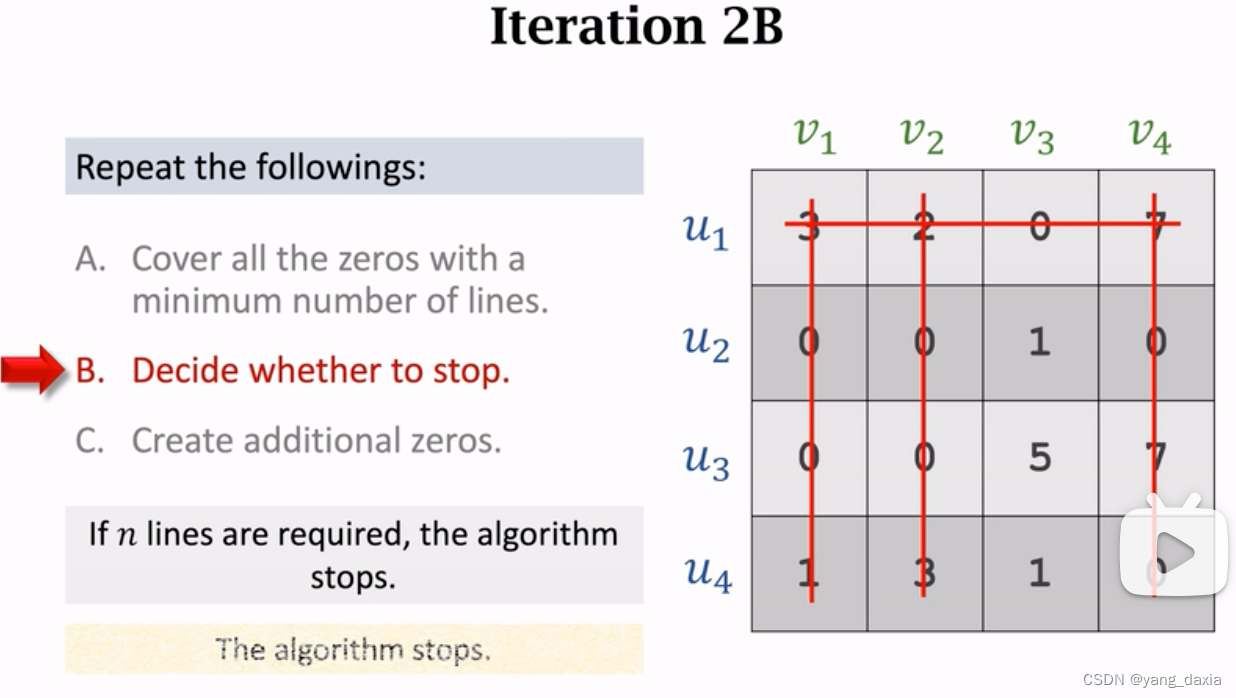
• 最大匹配结果可能不止1中，如5，2，3和5， 0， 5都是15。
  

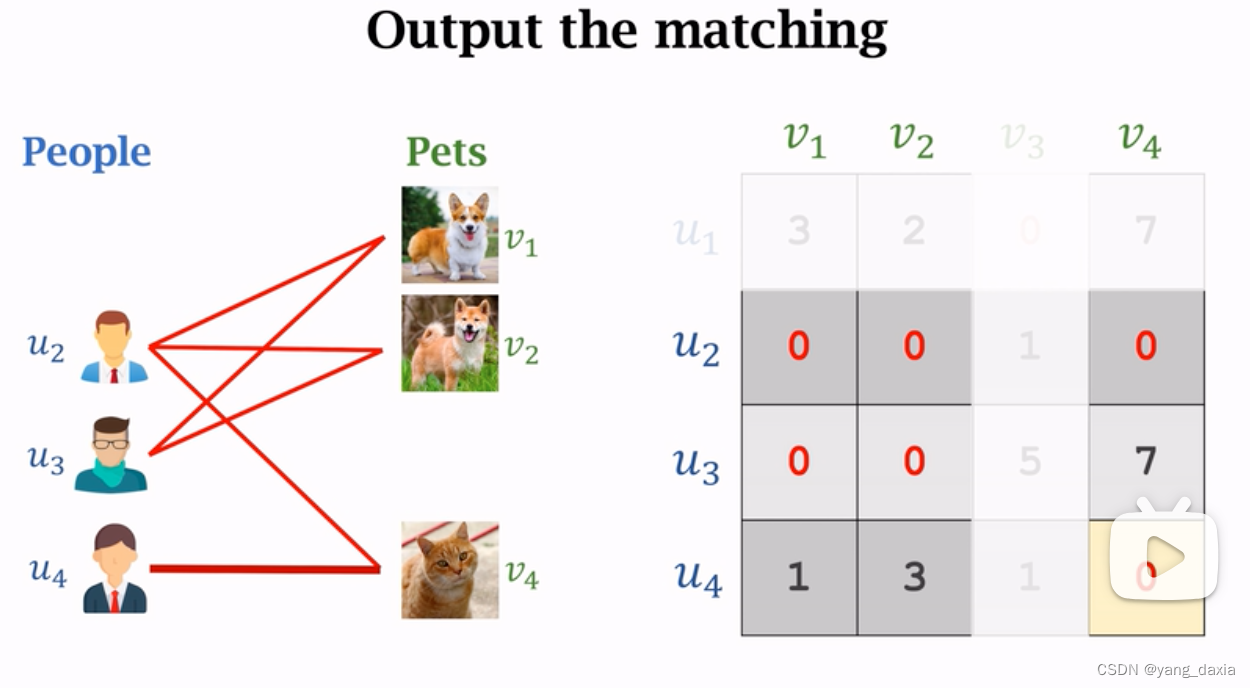
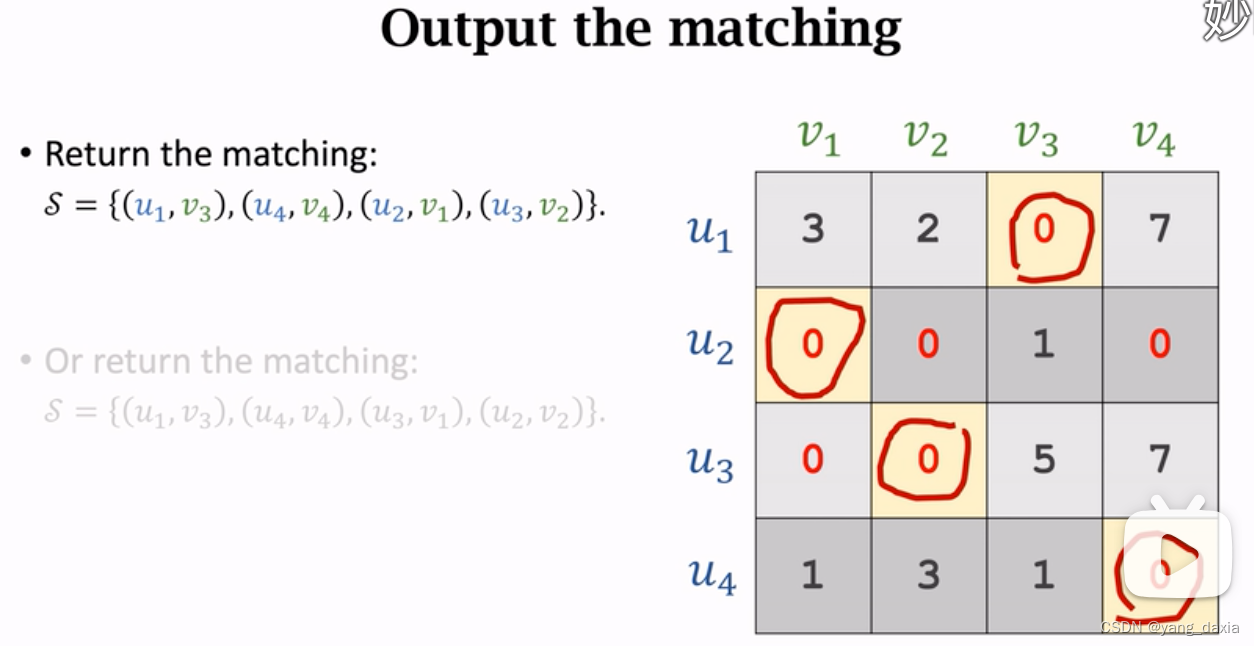
• 如果uv节点不一致，可以通过补几个虚拟节点，权重设置为0，使得uv节点数量一致，那就可以用匈牙利算法求解了。

稳定婚配算法

• 一种特殊的2分图匹配问题
• 边由权重变成了顺序，而且是双向的
• 可以用gale-shapely算法求解
• 时间复杂度为O(n^2)

代码实现

• 通过找增广路径的方式进行求解
• 非匹配点出发，到非匹配点截至，中间为非匹配与匹配交替出现，然后变换状态即可。
• KM算法是加了权重的匈牙利算法，先把左边赋值最大权重，然后如果冲突，左边-detla, 右边+detla的操作，再通过增广路径求解。detla为lx+ly-weight
  https://blog.csdn.net/sidnee/article/details/106298615

https://blog.csdn.net/qq_37457202/article/details/80161274

参考：
https://www.bilibili.com/video/BV1G54y157HA/?spm_id_from=333.788&vd_source=d141bc07699831d8053b781fd6944d5f