常见智力题汇总
- 扔瓶子问题
- 扑克牌问题
- 出队问题
- 烧绳子问题
- 赛马问题
- 求出前三名
- 求出前五名
- 接水问题
- 种树问题
- 硬币问题
- 宝石问题
- 核酸检测问题
笔者最近面试遇到了好几道智力题,这些题目特点就是如果没有见过,很难第一时间思考得到答案,因此笔者面试也就栽在了上面,所以本文来整理一波常见的智力题,以防后续面试再遇到。
相关智力题给出的都是网上的参考答案,未必完全正确,大家理性看待。
扔瓶子问题
题目: 给你两瓶矿泉水,总共一百层楼,咋找到能把矿泉水摔碎的临界点楼层,未摔碎可以去一楼捡回来,请说出至少三种方法 。
- 二分法:将一瓶矿泉水标记为水瓶A,另一瓶标记为水瓶B。首先,在50楼处摔破水瓶A。如果水瓶A碎了,那么临界点楼层在50楼以下;如果水瓶A没碎,那么临界点楼层在50楼以上。然后,根据摔碎的结果,对所在楼层范围内的楼层再次进行二分查找,重复以上步骤,直到找到临界点楼层。
- 等差递增法:将一瓶矿泉水标记为水瓶A,另一瓶标记为水瓶B。首先,在第10层楼摔破水瓶A,然后在第20层楼摔破水瓶A,接着在第30层楼摔破水瓶A,以此类推,每次递增10层。当水瓶A摔碎时,可以确定临界点楼层的范围,然后利用第二瓶矿泉水在该范围内逐层测试,直到找到临界点楼层。
- 三分法:将一瓶矿泉水标记为水瓶A,另一瓶标记为水瓶B。首先,在34楼处摔破水瓶A,然后根据摔碎的结果,如果水瓶A碎了,临界点楼层在1楼到33楼之间;如果水瓶A没碎,临界点楼层在34楼到66楼之间。然后,在临界点楼层范围内的中间楼层(例如,摔破水瓶A的楼层与上次摔破水瓶A的楼层的平均值)摔破水瓶A,重复以上步骤,直到找到临界点楼层。
扑克牌问题
问题: 52张扑克牌抽三张牌,抽到三张一样的概率、抽到同花顺的概率。
- 抽到三张一样的概率:
- 对于三张一样的情况,有4种可能,即选择一种花色,然后从该花色中选择三张牌。每种花色有13张牌,因此概率为:
- P(三张一样) = 4 * C(13, 3) / C(52, 3)
- 对于三张一样的情况,有4种可能,即选择一种花色,然后从该花色中选择三张牌。每种花色有13张牌,因此概率为:
- 抽到同花顺的概率:
- 对于同花顺,有10种可能的组合,即A2345、23456、34567、45678、56789、678910、78910J、8910JQ、910JQK和10JQKA。每种组合有4种花色,因此概率为:
- P(同花顺) = 10 * 4 / C(52, 3)
- 对于同花顺,有10种可能的组合,即A2345、23456、34567、45678、56789、678910、78910J、8910JQ、910JQK和10JQKA。每种组合有4种花色,因此概率为:
出队问题
问题: 100个人,排一列,奇数出列,剩下的人以此类推,最后一人在第一次排列第几位 。
思路:
- 第一次去掉奇数后,剩下2、4、6……96、98、100,所有的数字都是2=2的1次方的整数倍;
- 第二次去掉奇数项后,剩余的数为4、8 、12、 16……92、96、100,均是4=2的2次方的整数倍;
- 第三次去掉奇数项后,剩余的数应为8=2的3次方的整数倍的偶数,即是8、16、24、32、40、48、56、64、72、80、88、96;
- 第四次去掉奇数项后,剩余的数为16=2的4次方的整数倍的偶数,即是16、32、48、64、80、96;
- 第五次去掉奇数项后,剩余数为32=2^5的整数倍的偶数,即是32、64、96;
- 最后一次去掉奇数项,则剩余64.
烧绳子问题
问题: 燃烧一根不均匀的绳子需要一小时,怎么做才能问如何度量出半个小时,45分钟,75分钟?
思路:
度量半个小时:
- 第一个问题度量半个小时时最简单的,绳子虽然是不均匀的,但是一根绳子完整烧完所用的时间是固定的。从两端烧绳子,等绳子全部烧完所用的时间就是半个小时。
度量15分钟:
- 已经可以度量出半个小时与一个小时了,所以想要度量出45分钟与75分钟只需要度量出15分钟就可以了。
- 15分钟怎么度量的方法就是将半个小时的绳子从两端烧,绳子烧尽时所用的时间就是15分钟。而我们只有不均匀一个小时的绳子,从绳子两端烧尽可以获得半个小时,但是这根绳子不能用来进行15分钟的度量了,所以一个绳子是度量不出15分钟的,解决问题需要两根绳子
- 取两根绳子分别编号1和2,绳子1从两端开始烧,绳子2从一段开始烧。当绳子烧尽时,熄灭绳子2。此时绳子2燃烧尽所需要的时间就是半个小时,从绳子2两端烧的话燃尽就是15分钟。关键点15分钟已经可以度量出来的了,那么剩下的问题就迎刃而解了。
具体解法如下:
- 度量30分钟:取一根绳子,从两端燃尽所欲要的时间就是半个小时。
- 度量15分钟:取两根绳子,第一根从一段燃烧,另二根从两端同时燃烧。当第二根燃尽的时候,将第一根剩余绳子从两端燃烧,第一根绳子剩余从两端燃烧耗尽所需要的时间就是15分钟。
- 度量45分钟:取两根绳子,采用上述方法所需的总时间就是45分钟(30+15)
- 度量75分钟: 取三根绳子,其中两根采用上述方法得到燃尽需要半个小时的绳子,然后从两端烧燃尽需要15分钟,取第三根绳子从一段烧,总共需要75分钟(15+60).
赛马问题
求出前三名
问题一:25匹马,5个跑道,最少比多少次能比出前3名?
答案: 7次
解答过程:
- 25 匹马随机分成5组,每组比赛一次,也即总共比5次,先看一下每组马的快慢情况

- 由于我们只需要找出最快的三匹马,因此把肯定不会选上的马淘汰掉,即每组跑的最慢的两匹马

3. 将每组跑的最快的一匹马进行1次比赛,这样我们就可以选出25匹马中跑的第一快的马
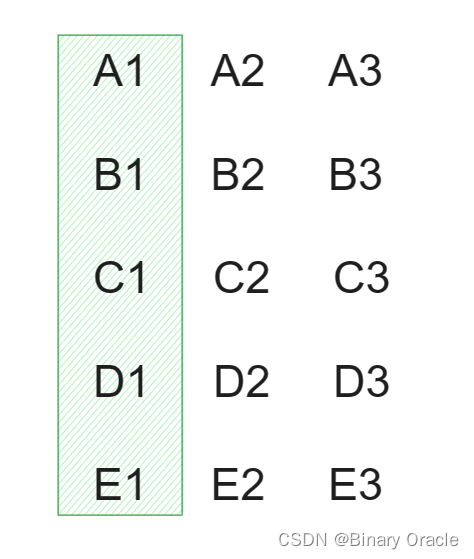
4. 此时可知A1是跑的最快的一匹马,B1和A2可能是跑的第二快的马,C1,B2 和 A3 可能是跑的第三快的马;让B1,A2,C1,B2 和 A3 共同比赛一次,可以计算出跑的第二快和第三快的马。
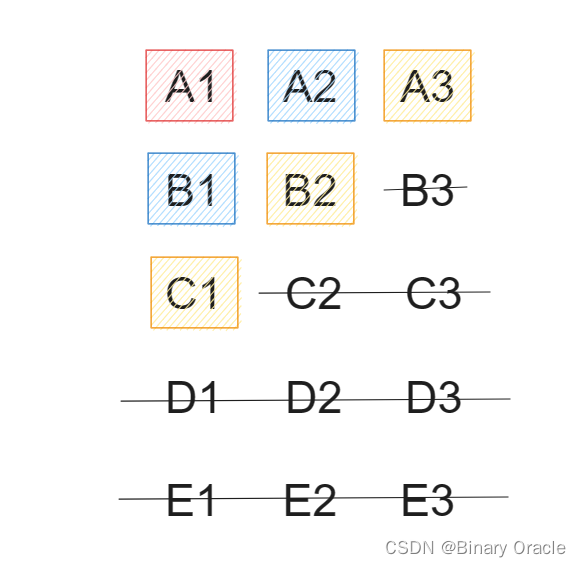
求出前五名
题目二:25匹马,5个跑道,最少比多少次能比出前5名?
答案: 最少8次,至多9次
解答过程:
- 25 匹马随机分成5组,每组比赛一次,也即总共比5次,先看一下每组马的快慢情况

2. 由于我们只需要找出最快的五匹马,因此把肯定不会选上的马淘汰掉,E1,D2 ,C3 和 B4 最好的排名就是第五,所以比他们跑的慢的马都淘汰掉
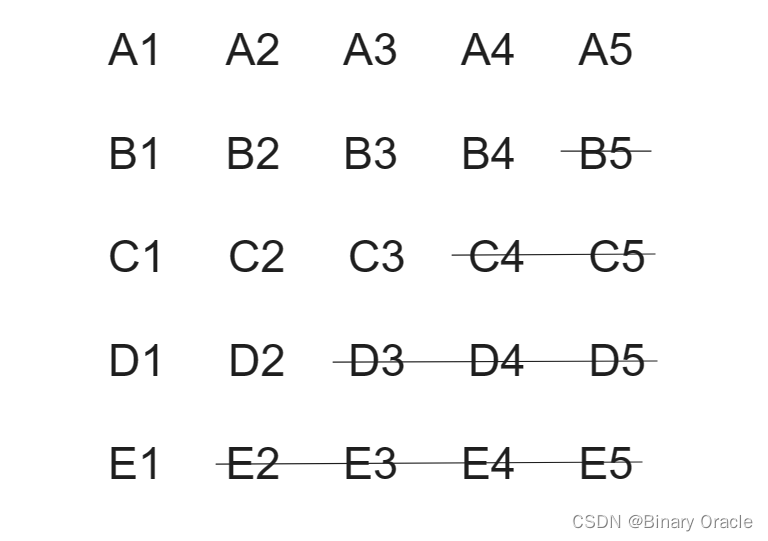
- A1 是跑的最快的一匹马,下面我们求解出跑的第二和第三名,第二名可能是B1或A2,第三名可能是C1,B2或者A3,让他们五个跑一次,算出第二和第三
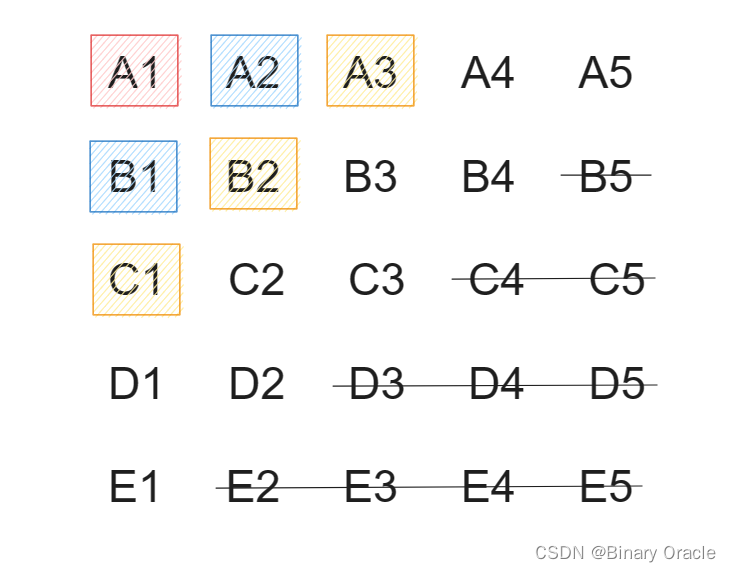
第四名和第五名的计算,需要根据情况分类讨论:
- 假设1,2,3 名都处于不同的分组中,并且A2在上一轮比赛中得到了第4名的成绩,那么可知A2最好的情况也是总排名的第五名,所以后面的都可以淘汰掉了;B2同理,最好的总排名是第4名,那么B3最好的总排名就是第五名,因此后面的都可以淘汰掉了。
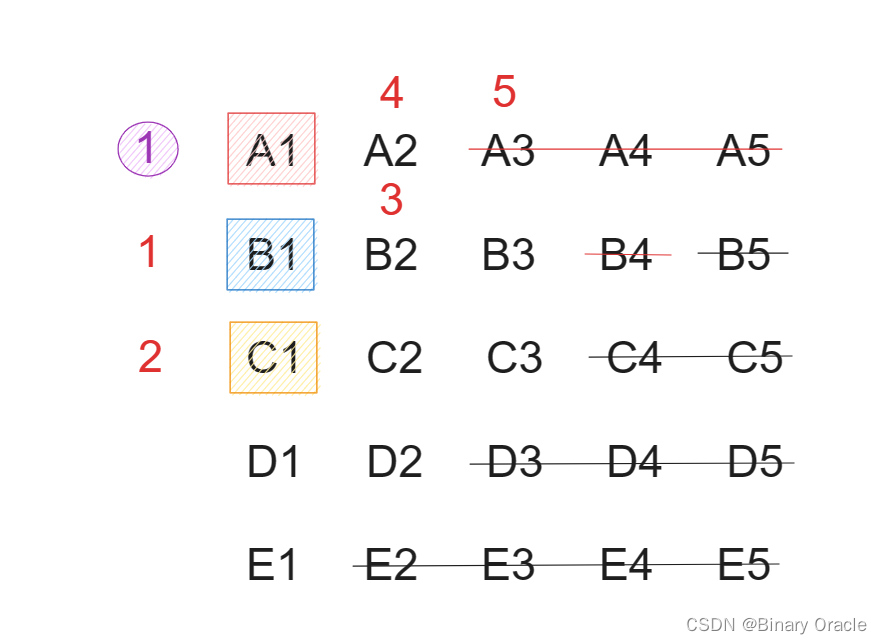
情况1下,剩余8匹马,五名先选5匹马出来跑一次,保留前两名,再利用前两名和剩余3匹马组成五匹马,再跑一次,最终可以计算出第四名和第五名。因此情况1需要9次比赛,才能算出最快的五匹马。
情况1的变种就是A2上一轮跑了第3,A3跑了第4,B2跑了第5,此时通过排除会发现只剩7匹马,但是依然需要两轮同上的比赛才能计算出第四和第五名。
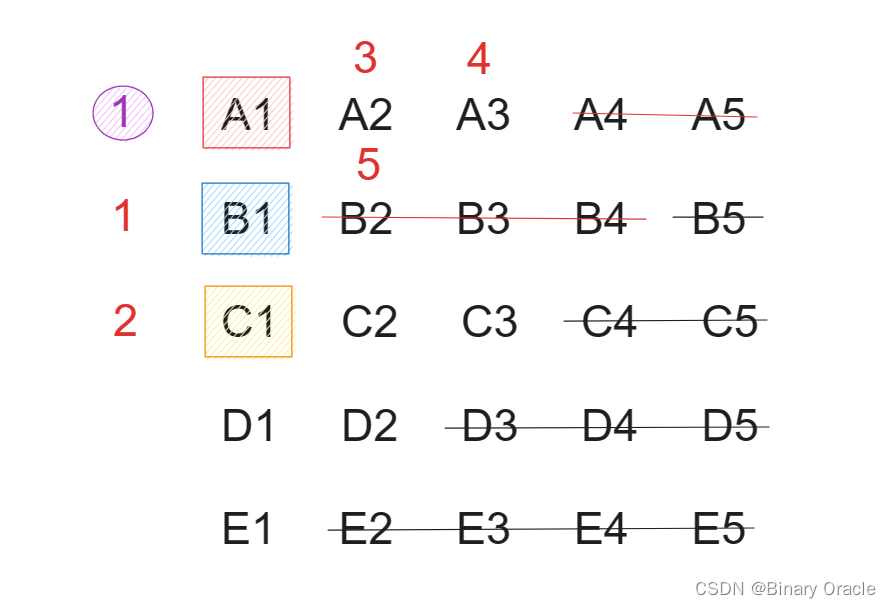
- 前三名都在同一组,此时通过排除不可能为第四和第五名的马后,会发现只剩下了4匹马,所以我们只需要在来一轮比赛,就可以计算出第四名和第五名。因此情况2,总共需要8轮比赛。
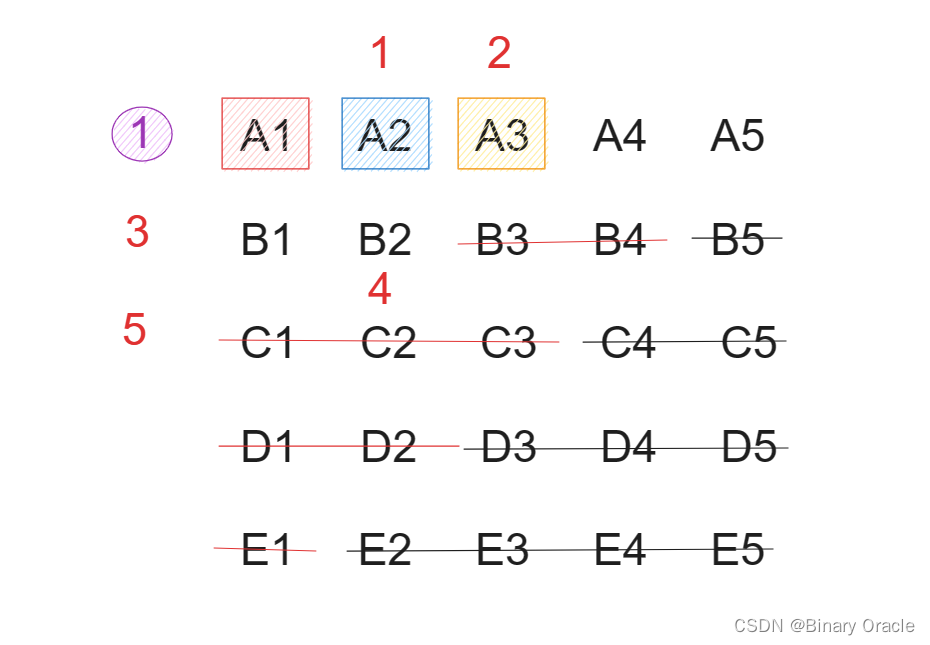
- 前两名位于同一组内,经过排除后,会发现剩余的马匹数量小于5,因此一轮比赛即可计算出最终结果。因此,情况3最终也只需要8轮计算。
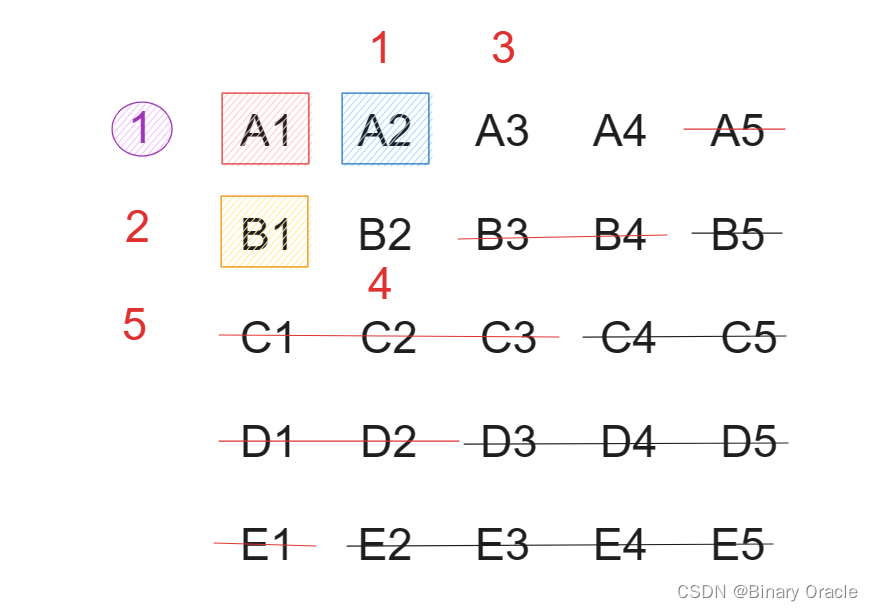
更加详细的推导过程参考此文
接水问题
问题: 用5L和6L的杯,没有刻度,怎么量出3L的水
解答:
- 6L的杯先接满水,然后用6L的杯倒满5L的杯,此时6L杯剩1L水
- 清空5L的杯,然后将6L的杯剩余的1L水倒入5L的杯
- 6L的杯先接满水,然后用6L的杯倒满5L的杯,此时6L杯剩2L水
- 清空5L的杯,然后将6L的杯剩余的2L水倒入5L的杯
- 6L的杯先接满水,然后用6L的杯倒满5L的杯,此时6L杯剩3L水
问题: 3升的杯子和5升的杯子怎么得到4升的水?
解答:
- 5L的杯先接满水,然后用5L的杯倒满3L的杯,此时5L杯剩2L水
- 清空3L的杯,然后将5L的杯剩余的2L水倒入3L的杯
- 5L的杯先接满水,然后用5L的杯倒满3L的杯,此时5L杯剩4L水
种树问题
问题: 四棵树怎么种才能使任意两颗之间距离相等
思路:
- 搞个正四面体的土堆,把树栽在4个顶点,其实也就是问4个点间距离两两相等,平面内是不可能的,只能考虑立体了
硬币问题
问题: 100枚硬币,甲和乙轮流拿,每次只能拿1-5枚,最后拿完硬币的人赢,让甲先手拿,怎么拿才能保证甲最后一定赢?
解答:
- 需要甲赢,也就是说最后需要让甲拿完剩下的球,那么对于乙来说,就要求最后一轮拿不完剩下的球,而且无论怎么拿,剩下的球都会被甲一次性拿完。
- 再结合题目条件思考: 双方一次性只能拿1~5个球,那么最后轮到乙拿的时候应该还剩6个硬币。
- 在球的总数是6的倍数的情况下,后手者每次只需要拿
6 - 先手者所拿球个数,即可确保赢得最终的胜利 - 又因为此处球的总数为100 ,比6的倍数96多4个球,因此甲在一开始只需要拿4个球,后面每次只需要拿
6 - 乙所拿球个数, 即可确保赢得最终的胜利
总结:
- 除尽的情况下,后拿者赢;(后者每次拿的个数都是除数 - 前者拿的个数)
- 除不尽的情况下,先拿者赢;(先拿者先拿出被除数对除数的余数,然后的每一个回合,拿出除数-前者拿出的个数)
详细推导过程可参考
宝石问题
问题: 有2堆宝石,A和B一起玩游戏,假设俩人足够聪明,规则是每个人只能从一堆选走1个或2个或3个宝石,最后全部取玩的人获胜,假设2堆宝石的数目为12和13,请问A怎么可以必胜?
解答:
- 先取获胜的情况:总个数不能整除时,余数为一次可取的个数
- 后取获胜的情况:总个数能整除时
- 只有一堆时,12时后取获胜,13时先取获胜
- 两堆时,A先取12堆
本题和硬币问题思路一致。
核酸检测问题
问题: 假如现在有100个人,有一个人感染了新冠肺炎,问只检测一轮(即统一去做,每个人可以做多次,但是不能等到检测结果出来再去做)的情况下,如果用最少的试剂定位到感染者?
答案:
对1~100名进行二进制编号:因为2^6 < 100 < 2^7。所以用7bit的二进制进行编号:
- 1号: 000 0001
- 2号: 000 0010
- 3号: 000 0011
- 4号: 000 0100
- 5号: 000 0101
- 6号: 000 0110
- 7号: 000 0111
- …
- 100号: 110 0100
所以:
- 试剂瓶1:需要编号中bit0 为1的人一起去做检测,即1,3,5 …
- 试剂瓶2:需要编号中bit1 为1的人一起去做检测,即2,3,6,7 …
- 试剂瓶3:需要编号中bit2 为1的人一起去做检测,即4,5,6 …
- …
- 试剂瓶7:需要编号中bit6为1的人一起去做检测 …
最后,阳性为1,阴性为0,将试剂瓶的结果组成一个二进制数,试剂瓶7位最高位,试剂瓶1为最低位,得到的数字就是确认的那位。
不断更新中 … ,也欢迎各位留言补充自己遇到的智力题。