题目描述

给定一个正整数 n ，将其拆分为 k 个 正整数 的和（ k >= 2 ），并使这些整数的乘积最大化。

返回 你可以获得的最大乘积 。

示例 1:

输入: n = 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1。

示例 2:

输入: n = 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。

思路

动态规划解决的经典类型题目之一。首先要明确dp数组的含义，再找出状态转移方程并初始化，迭代下去即可得出解。

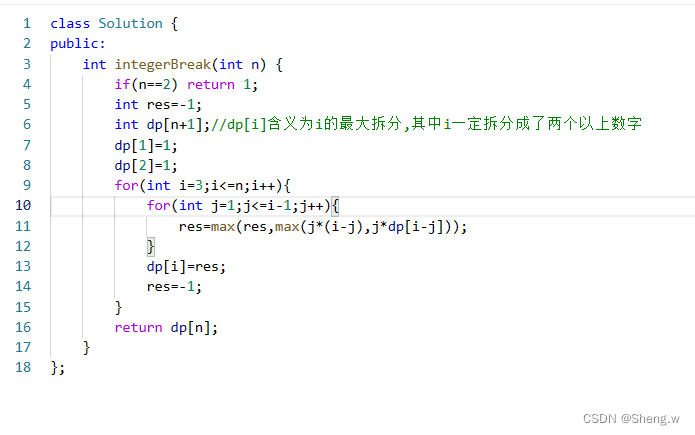
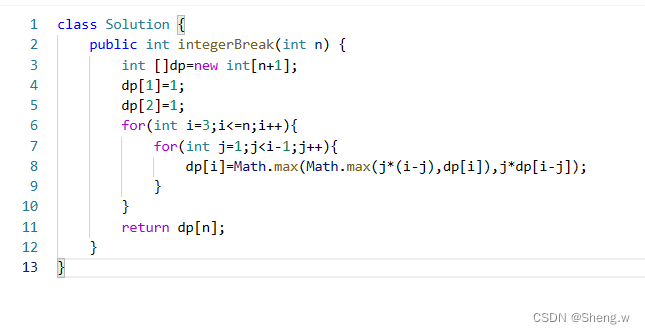
dp[i]: 分拆数字i，可以得到的最大乘积为dp[i]。注意，数字 i 必须拆分，即 i 不可以不拆。

状态转移方程：要求dp[i]，i可以拆分成两个、三个或者更多，如果拆分成两个，则dp[i]=j*(i-j)，其中j在0到i之间；如果拆分成三个以上，则dp[i]=j*dp[i-j]；我们只需在二者之间取较大值即可。得：

        dp[i] = max((i - j) * j, dp[i - j] * j)

初始化：根据状态转移方程和dp数组的定义易知dp[1]=1,dp[2]=1;

解法

C++版本

Java版本