1.基本概念
图(Graph)是一种较线性表和树更为复杂的非线性结构。是对结点的前趋和后继个数不加限制的数据结构,用来描述元素之间“多对多”的关系(即结点之间的关系是任意的)。
一个图G = (V,E)由顶点(vertex)集V(G)和边(edge)集E(G)组成。E中的每一条边连接V中两个不同的顶点。
1、有向图(digraph)
如果图中每一条边上两个顶点都是有序的,那么图就叫做是有向图(directed graph)。 可以用带尖括号的有序点对<ν,ω>来表示有向图的一条边,其中ν,ω∈V(G)。 有向图中的边都是有方向的,称之为有向边。对于有向边来说,<ν,ω>和<ω,ν>表示的是两条方向相反的边。 有向图中的边也可称之为弧(arc),ν可称之为弧尾(tail)或初始点(initial node),ω可称之为弧头(head)或终端点(terminal node)。

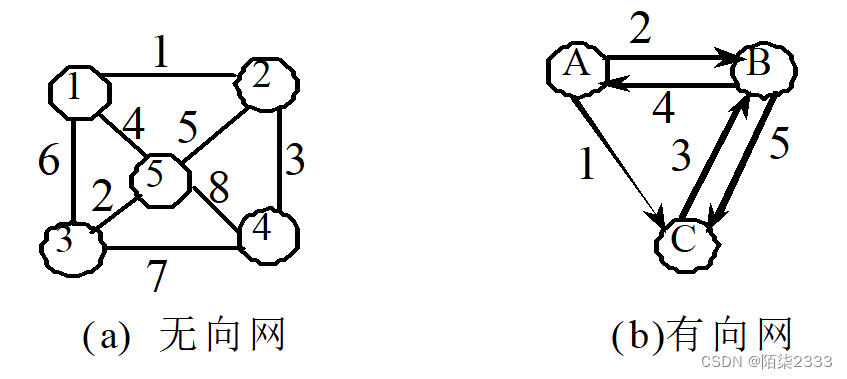
V(G1)={ν1,ν2,ν3,ν4}
E(G1)={<ν1,ν2>,<ν2,ν1>,<ν3,ν1>,<ν3,ν4>,<ν2,ν4>}
2、无向图(undigraph)
如果图中每一条边上两个顶点都是无序的,那么图就叫做是无向图(undirected graphy) 可以用带圆括号的点对(ν,ω)来表示无向图的一条边,其中ν,ω∈V(G)。 无向图中的边都是没有方向的,称之为无向边。其中,(ν,ω)和(ω,ν)表示的是同一条边。
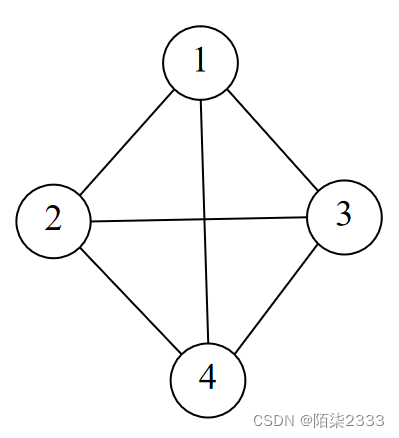
V(G2)={1,2,3,4}
E(G2)={(1,2),(1,3),(1,4),(2,3),(2,4),(3,4)}
3、邻接点
如果图G = (V,E)为无向图,若存在一条边(v,v’)∈E(G),则称点v和v’互为邻接点,即v和v’相邻接,边(v,v’)依附于顶点v和v’,或者说(v,v’)和顶点v和v’相关联。 如果图G = (V,E)为有向图,若存在一条弧 <v,v’> ∈E(G),则称顶点v邻接到顶点v’,顶点v’邻接自顶点v,弧 <v,v’>和顶点v和v’相关联。

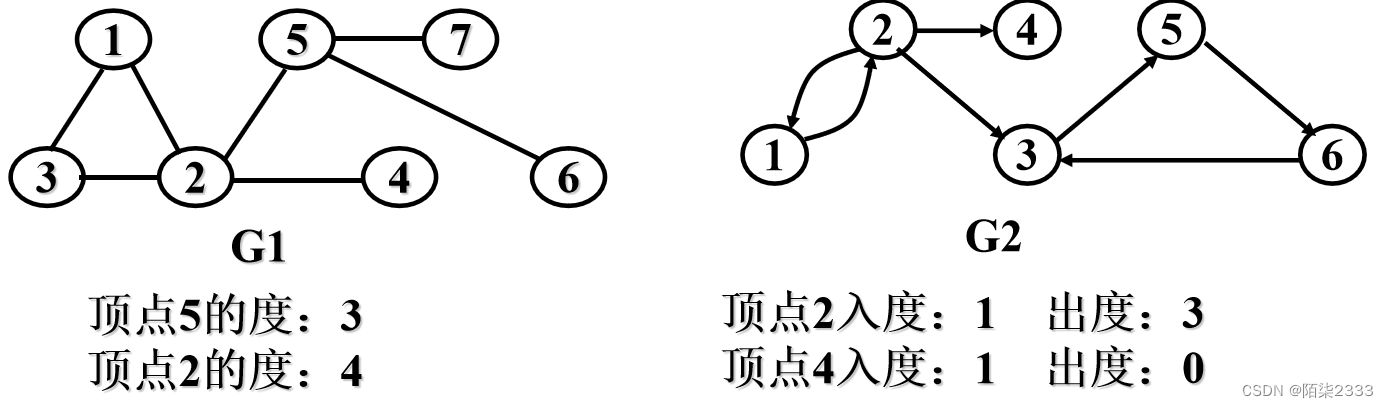
4. 度、入度和出度
顶点的度 :顶点v的度TD(V)=和v相关联的边的数目
在无向图中, 顶点所具有的边的数目称为该顶点的度

入度和出度:
对于有向图G={V,{A}}:
v的入度ID(v) = 以顶点v为头的弧的数目
v的出度OD(v) = 以顶点v为尾的弧的数目
有向图中,顶点的度 = 入度 + 出度
一个有n个顶点,e条边的图满足下列等式:
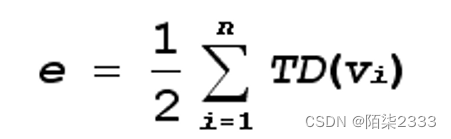
即边(或弧)的总数 = 各个顶点的度的总数的一半
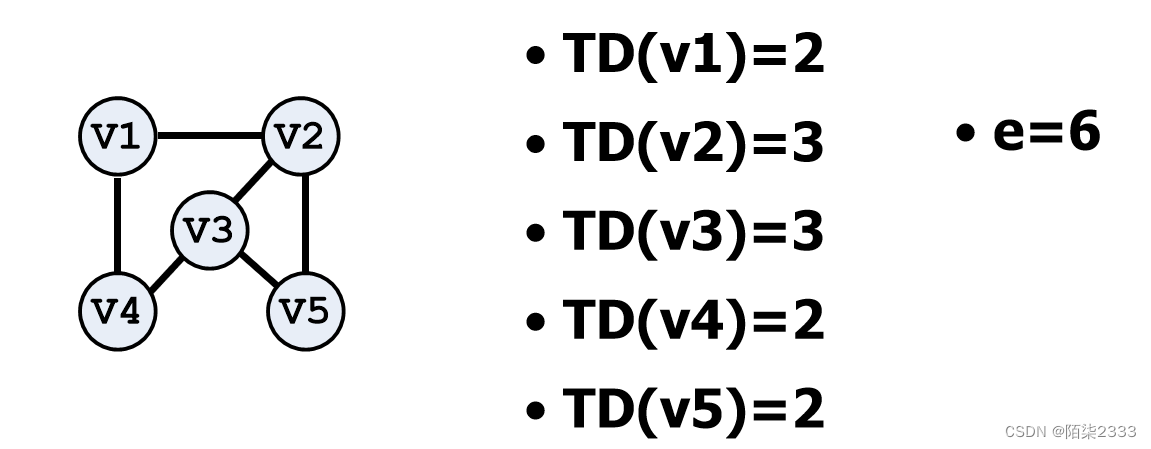
5、完全图、稀疏图与稠密图
设n为顶点数,e为边或弧的条数
对无向图有:0 ≤ e ≤ n(n-1)/2
有向图有:0≤ e ≤ n(n-1)
证明:每个顶点至多有n-1条边与其它的n-1个顶点相连,则n个顶点至多有n(n-1)条边。但每条边连接2个顶点,故最多为n(n-1)/2。
完全图:边达到最大的图
无向完全图:具有n(n-1)/2条边的简单图称为无向完全图
有向完全图:具有n(n-1)条边的有向图。
稀疏图: 边或弧很少的图。
稠密图: 边或弧很多的图。
6. 路径与回路
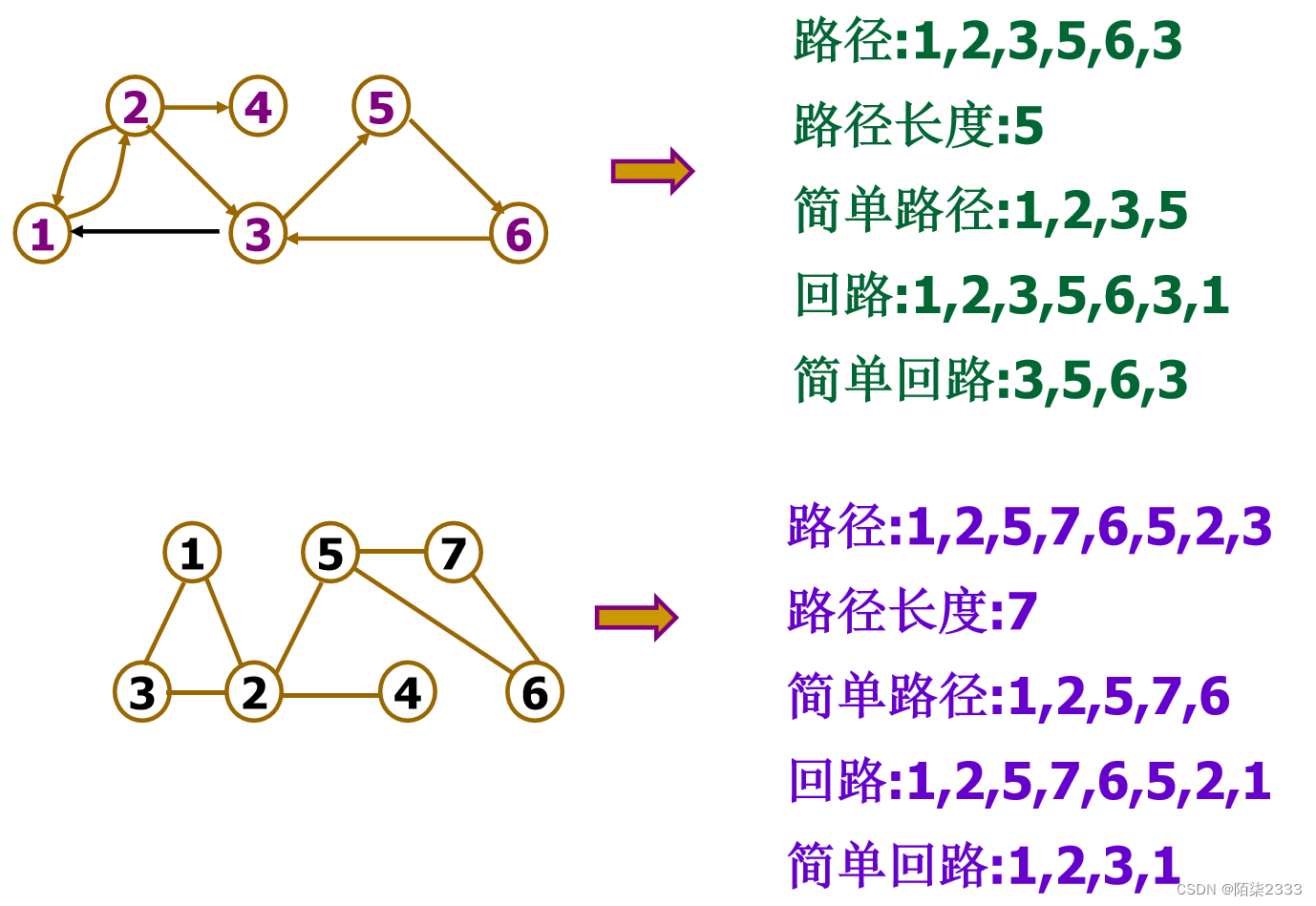
路径:在图G 中,如果存在一个顶点序列(ω1,ω2,ω3,…,ωN),使得(ωi,ωi+1)∈E(G),1 ≤ i < N,则称这个顶点序列为顶点ω1到顶点ωN的一条路径(path)。
G1中{ 1,2,5,7 }是一条路径
G2中{ 1,2,3,5,6 }是一条路径
如果G是有向图,则路径也是有向的
路径长度:路径上边或弧的数目或沿路径各边权值之和
回路:第一个顶点和最后一个顶点相同的路径
简单路径:序列中顶点不重复出现的路径(即不含回路的路径)
简单回路:除了第一个顶点和最后一个顶点外,其余顶点不重复出现的回路叫简单回路
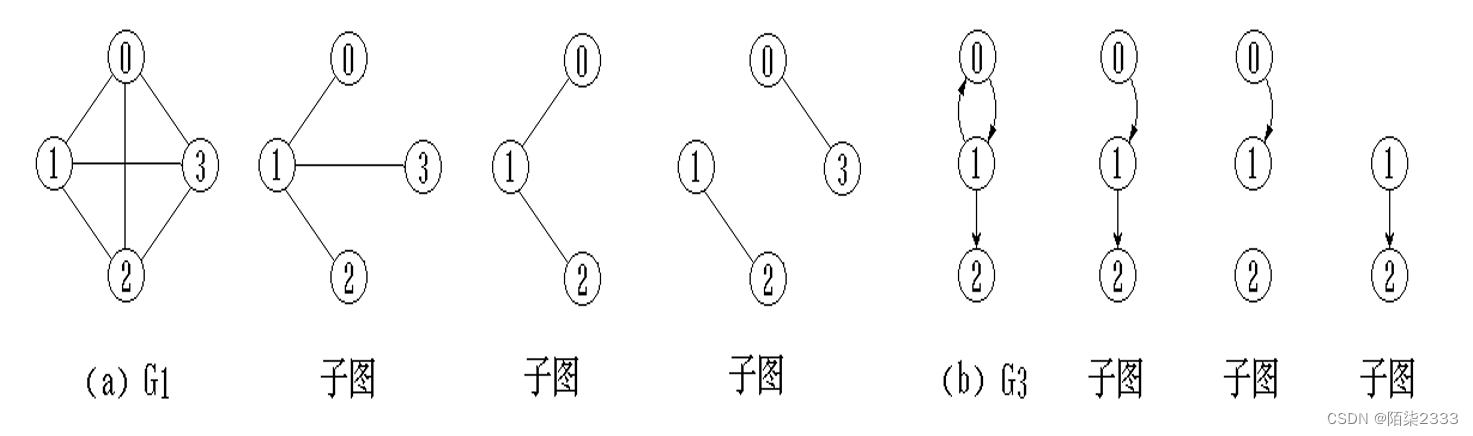
7、子图
设有两个图 G=(V, E) 和 G’=(V’, E’)。若 V’真包含于 V 且 E’真包含于E, 则称 图G’ 是 图G 的子图。
8、连通图
连通图 :在无向图G中,如果从顶点v到顶点v’有路径,则称v和v’是连通的
如果对于图中的任意两个顶点vi和vj都是连通的,则称G是连通图
是否连通是对无向图来说的
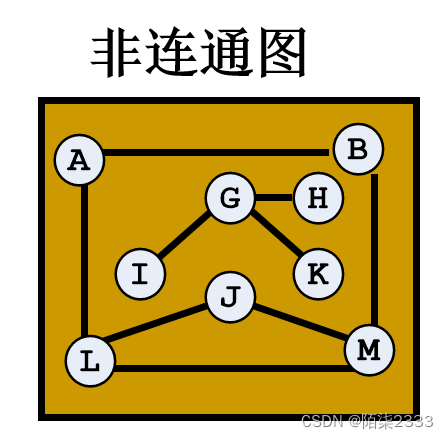
连通分量 :
无向图中的极大连通子图 连通图只有一个连通分量,就是它本身,而非连通图有多个连通分量。
强连通图 :
在有向图G中,如果每一对vi,vj,都存在从vi到vj和从 vj到vi的路径的路径,则称G为强连通图
是否强连通是对有向图来说的
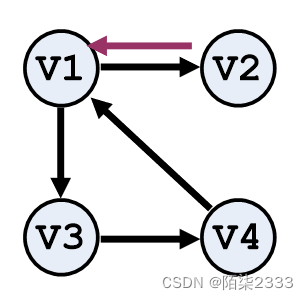
强连通分量 :
有向图中的极大强连通子图
显然,强连通图只有一个强连通分量,即本身
非强连通图有多个强连通分量。
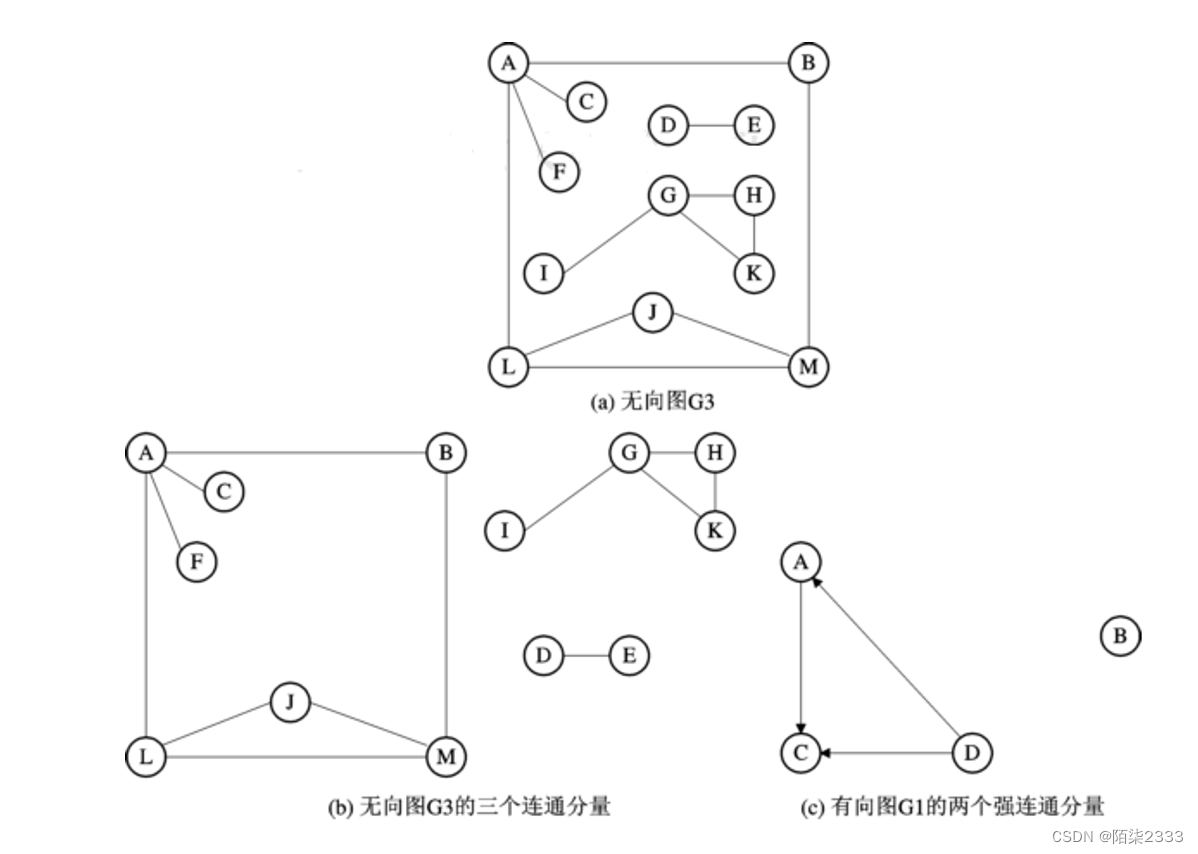
有n个顶点的有向强连通图最多有n(n-1)条边(构成一个有向完全图的情况);最少有n条边(n个顶点依次首尾相接构成一个环的情况)。
9、生成树
生成子图 :包括所有顶点的子图,成为生成子图
生成树 若生成的子图是树,则称为生成树。
一个连通图的生成树是指一个极小连通子图,它含有图中的全部顶点,但只有足以构成一个树的n-1条边。
一颗有n个顶点的生成树有且仅有n-1条边,如果图中多于n-1条边,则一定有回路。
如果一个图具有n个顶点且边数小于n-1条,则该图一定是非连通图。
一个连通图的生成树不唯一。
10、网
权:某些图的边或弧具有与它相关的数, 称之为权。权可以代表一个顶点到另一个顶点的距离、耗费等。
网:这种带权连通图一般称为网。
若无向图G中每一条边都有一个对应的数,则称G为带权图或网。类似的,边上带权的有向图称为有向网。