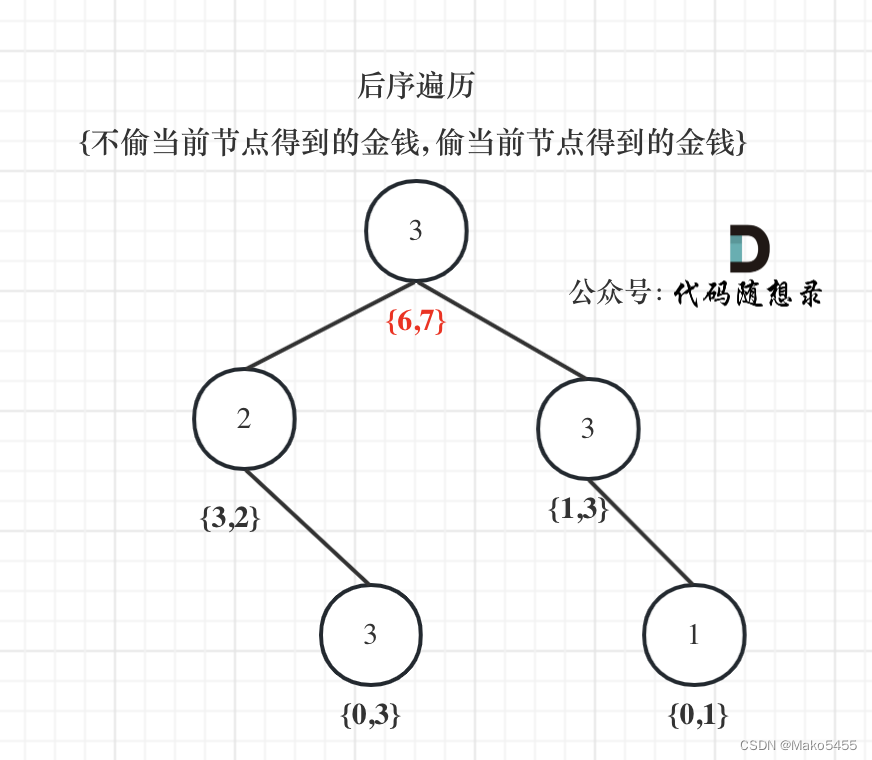
题目要求如上，这里可以有两种解题思路，一种是利用动态规划去求解，一种是用贪心去求解。
首先看下动态规划的方法。

用动归去解决

动态规划最重要的就是要想出来递推公式（这个真的很难），但是一旦想清楚递推公式，写代码就很轻松，其实感觉这里的算法题都是这种，主要考察的是思路而不是工程能力。
首先我们观察题目发现，这里说明了每天最多只能持有一只股票，因此这里的每天的状态只有两种：

• 不持有股票
• 持有股票

那我们最后只有返回两种状态下的最大利润就可以了，有时候想不明白可以先想3天的情况，会更好推理。我们定义：

• $dp[i][0]$ 表示第i天不持有股票所获得的最大利润
• $do[i][1]$ 表示第i天持有股票所获得的最大利润

先来看不持有股票的情况：

1. 前一天持有股票但今天卖出了，此时截止今天的最大收益为：dp[i-1][1] + prices[i]
2. 前一天没有持有股票而且今天也不买，此时截止今天的最大收益为：dp[i-1][0]

因此对于没有持有股票来说，递推公式为：
$$dp[i][0]=max(dp[i-1][1]+prices[i],dp[i-1][0])$$
再来看持有股票的情况：

1. 前一天持有股票今天也不能买了，此时截止今天的最大收益为：dp[i-1][1]
2. 前一天没有持有股票今天买入股票，此时截止今天的最大收益为：dp[i-1][0] - prices[i]

因此对于没有持有股票来说，递推公式为：
$$dp[i][1]=max(dp[i-1][0]-prices[i],dp[i-1][1])$$
对于初始状态：$dp[0][0]=0,dp[0][1]=-prices[0]$
有了初始状态和递推公式，代码岂不是手到擒来：

def solve(prices):
    days = len(prices)
    if days == 0:
        return 0
    rst = [[0, 0]] * days
    rst[0][0] = 0  # 第i天不持有股票能获得的利益
    rst[0][1] = -prices[0]  # 第i天持有股票能获得的利益

    for i in range(1, days):
        rst[i][0] = max(rst[i - 1][0], rst[i - 1][1] + prices[i])
        rst[i][1] = max(rst[i - 1][1], rst[i - 1][0] - prices[i])
    return max(rst[-1])

贪心思路

真的觉得贪心就是脑筋急转弯。贪心思路很好理解，但是一般很难想到。
既然我的目的是计算出最大收益，那我只要保证我每天的收益都是最大的就可以了。那我怎么保证呢？只要我每天的收益都是正的，那就是最大收益咯。
$$rst=rst+max(0,p[i]-p[i-1])$$

代码也超简单：

def greed_solve(prices):
    rst = 0
    for i in range(1, len(prices)):
        rst += max(0, prices[i] - prices[i - 1])
    return rst