文章目录
- 目的:python实现one way ANOVA 单因素方差分析
- 1. 代码流程
- 2. python代码实现
- 0 主要的函数
- 1 加载数据
- 2 查看数据统计结果
- 3 数据处理及可视化
- 4 方差分析
- 4.1 模型拟合
- 4.2 单因素方差分析
- 5 Post Hoc t-test组间比较分析
- 6 根据定义自行分解计算对比调用函数的结果
- 7 获取F分布对应的P值
- 3. 方差分析公式及原理参考
目的:python实现one way ANOVA 单因素方差分析
1. 代码流程
a. 通过调用python的包来进行方差分析
b. 根据公式进行方差分析
c. 对比两种方法(工具包与手算)的结果,结果发现:一致
d. 最后附上方差分析的原理和计算公式
2. python代码实现
0 主要的函数

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy import stats # 里面有方差齐性检验方差
from statsmodels.formula.api import ols # 最小二乘法拟合
from statsmodels.stats.anova import anova_lm # 方差分析
import warnings
warnings.filterwarnings("ignore", category=FutureWarning)
warnings.filterwarnings("ignore", category=UserWarning)
1 加载数据
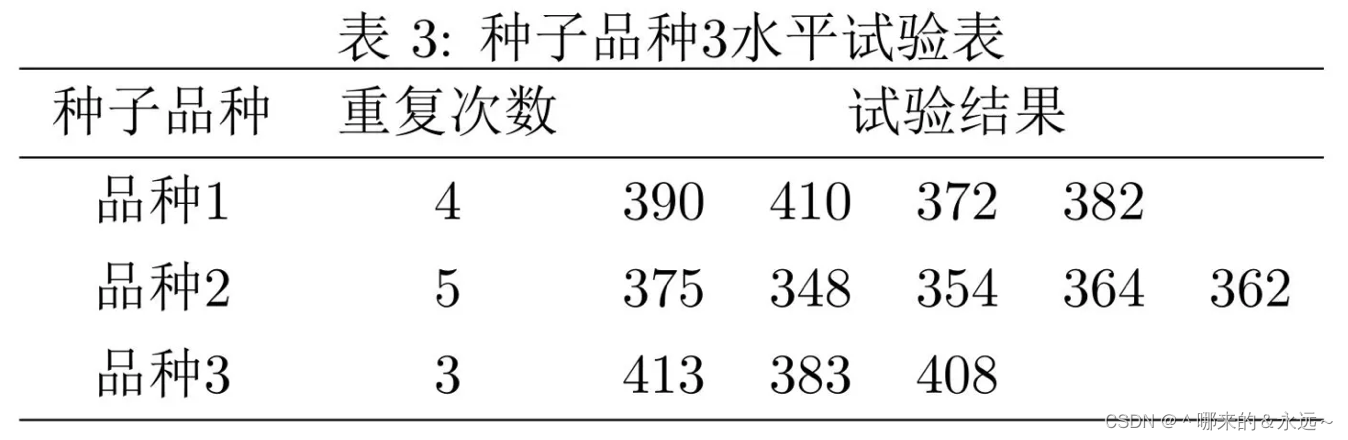
dataD = {'treat1':[390,410,372,382,None],
'treat2':[375,348,354,364,362],
'treat3':[413,383,408,None,None]}
data = pd.DataFrame(dataD)
data
| treat1 | treat2 | treat3 | |
|---|---|---|---|
| 0 | 390.0 | 375 | 413.0 |
| 1 | 410.0 | 348 | 383.0 |
| 2 | 372.0 | 354 | 408.0 |
| 3 | 382.0 | 364 | NaN |
| 4 | NaN | 362 | NaN |
2 查看数据统计结果
data.describe()
| treat1 | treat2 | treat3 | |
|---|---|---|---|
| count | 4.000000 | 5.000000 | 3.000000 |
| mean | 388.500000 | 360.600000 | 401.333333 |
| std | 16.114176 | 10.285913 | 16.072751 |
| min | 372.000000 | 348.000000 | 383.000000 |
| 25% | 379.500000 | 354.000000 | 395.500000 |
| 50% | 386.000000 | 362.000000 | 408.000000 |
| 75% | 395.000000 | 364.000000 | 410.500000 |
| max | 410.000000 | 375.000000 | 413.000000 |
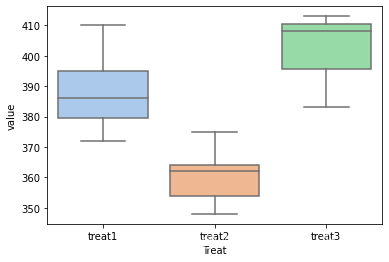
3 数据处理及可视化
我们为了方便计算,将所有的数据合成一列,并画一下箱线图看一下
data_melt = data.melt()
data_melt.columns = ['Treat', 'value']
print(data_melt)
Treat value
0 treat1 390.0
1 treat1 410.0
2 treat1 372.0
3 treat1 382.0
4 treat1 NaN
5 treat2 375.0
6 treat2 348.0
7 treat2 354.0
8 treat2 364.0
9 treat2 362.0
10 treat3 413.0
11 treat3 383.0
12 treat3 408.0
13 treat3 NaN
14 treat3 NaN
import seaborn as sns
# plt.figure(dpi=600)
sns.boxplot(data = data_melt, x = 'Treat', y = 'value',
palette = 'pastel', # 控制箱子颜色
)
4 方差分析
4.1 模型拟合
from statsmodels.formula.api import ols # 最小二乘法拟合
from statsmodels.stats.anova import anova_lm # 方差分析
from statsmodels.stats.multicomp import pairwise_tukeyhsd # post Hoc t_test
model = ols('value ~C(Treat)', data = data_melt).fit() # 最小二乘法拟合
# ols模型拟合的参数
print(model.params)
# 模型拟合的均值:
# mean_treat1 = 388.5
# mean_treat2 = 388.5 - 27.9 = 360.6
# mean_treat3 = 388.5 + 12.833 = 401.33
## 实际的均值:
# mean_treat1 = 388.500000
# mean_treat2 = 360.600000
# mean_treat3 = 401.333333
Intercept 388.500000
C(Treat)[T.treat2] -27.900000
C(Treat)[T.treat3] 12.833333
dtype: float64
无论是普通线性模型还是广义线性模型,预测的都是自变量x取特定值时因变量y的平均值。
print(model.summary())
OLS Regression Results
==============================================================================
Dep. Variable: value R-squared: 0.673
Model: OLS Adj. R-squared: 0.600
Method: Least Squares F-statistic: 9.257
Date: Thu, 30 Nov 2023 Prob (F-statistic): 0.00655
Time: 16:43:18 Log-Likelihood: -46.814
No. Observations: 12 AIC: 99.63
Df Residuals: 9 BIC: 101.1
Df Model: 2
Covariance Type: nonrobust
======================================================================================
coef std err t P>|t| [0.025 0.975]
--------------------------------------------------------------------------------------
Intercept 388.5000 6.910 56.224 0.000 372.869 404.131
C(Treat)[T.treat2] -27.9000 9.271 -3.010 0.015 -48.871 -6.929
C(Treat)[T.treat3] 12.8333 10.555 1.216 0.255 -11.044 36.710
==============================================================================
Omnibus: 0.469 Durbin-Watson: 2.839
Prob(Omnibus): 0.791 Jarque-Bera (JB): 0.509
Skew: 0.080 Prob(JB): 0.775
Kurtosis: 2.004 Cond. No. 3.80
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
4.2 单因素方差分析
anova_table = anova_lm(model, type = 2) # 方差分析
pd.DataFrame(anova_table) # 查看方差分析结果
| df | sum_sq | mean_sq | F | PR(>F) | |
|---|---|---|---|---|---|
| C(Treat) | 2.0 | 3536.050000 | 1768.025000 | 9.257393 | 0.006547 |
| Residual | 9.0 | 1718.866667 | 190.985185 | NaN | NaN |
参数解释:
-
df: degree of freedom 自由度:自由度是你现有数据中包含的可能性。- 例1:为什么当你求全班50个同学身高总和的时候自由度是49?
因为如果把学号1到学号49的同学身高全都固定下来, 比方说总和为83米,而全班50个人的身高总和,为84.7米,
那么第50个同学的身高必须为1.7米,没有任何自由变化的余地。 - 例2:假设有三个数字,A+B+C=10,假设A为任意数取8,B为任意数取2,那么c就是0 这个等式才能成立,这个等式当中有三个未知量,
但是可以有自由变换的数值只有两个,所以这个式子自由度就是3-1=2,所以样本当中能自由变化的数据个数叫做自由度。
对于本案例:
- K = 3: 共有3组,treat1,treat2,treat3。
- n = 12: 3组共有12个测量值
- df_C(Treat): K-1 = 3-1=2
- df_Residual: n-k = 12-3 = 9
- 例1:为什么当你求全班50个同学身高总和的时候自由度是49?
-
sum_sq: error sum of square 误差平方和- 表示实验误差大小的偏差平方和,在相同的条件下各次测定值xi对测定平均值x的偏差平方后再加和∑(xi-x)2
-
mean_sq: Mean Squared Error 均方误差- 均方误差是指参数估计值与参数真值之差平方的期望值
- 可以发现,treat组间存在显著性差异,p=0.006547 < 0.5
因为对比的组别超过三个,并且呈现出显著性差异,所以考虑使用事后检验(post hoc)进一步对比具体两两组别间的差异情况。
5 Post Hoc t-test组间比较分析
print(pairwise_tukeyhsd(data_melt['value'], data_melt['Treat']))
Multiple Comparison of Means - Tukey HSD, FWER=0.05
===============================================
group1 group2 meandiff p-adj lower upper reject
-----------------------------------------------
treat1 treat2 nan nan nan nan False
treat1 treat3 nan nan nan nan False
treat2 treat3 nan nan nan nan False
-----------------------------------------------
这里我们发现:
- Q:单因素方差分析结果显著,但事后t检验两两比较均不显著,这样的结果合理吗?
- A:合理,方差分析结果显著只说明组间可能存在显著差异,到底有无显著差异还要看事后比较
6 根据定义自行分解计算对比调用函数的结果
# 全部的算数平均数为:380.083
mean_all = ((390+410+372+382+375+348+354+364+362+413+383+408)/12)
# 3个品种的算数平均数分别为:388.5,360.6,401.33
print('总平均:\n', mean_all)
mean_k = data.mean(axis = 0)
print('组平均:\n', mean_k)
总平均:
380.0833333333333
组平均:
treat1 388.500000
treat2 360.600000
treat3 401.333333
dtype: float64
## 组内方差
SS_e = (390-388.5)**2 + (410-388.5)**2 + (372-388.5)**2+(382-388.5)**2+\
(375-360.6)**2+(348-360.6)**2+(354-360.6)**2+(364-360.6)**2+(362-360.6)**2+\
(413-401.3)**2+(383-401.3)**2+(408-401.3)**2
df_e = 12-3 # 自由度:共12个样本,3个水平
print("Residual sum_sq:", SS_e)
## 组间方差
SS_A = 4*(388.5-380.083)**2 + 5*(360.6-380.083)**2 + 3*(401.333-380.083)**2
df_A = 3-1 # 共3个水平
print("C(Treat):", SS_A)
Residual sum_sq: 1718.8700000000003
C(Treat): 3536.007500999999
## 计算F
MS_A = SS_A / df_A
MS_e = SS_e / df_e
F = MS_A / MS_e
print("MS_A:", MS_A)
print("MS_e:", MS_e)
print("F:", F)
MS_A: 1768.0037504999996
MS_e: 190.9855555555556
F: 9.257264222716081
7 获取F分布对应的P值
from scipy.stats import f #导入f
PR = f.sf(F, df_A, df_e)
print(PR)
m = df_A #设置自由度m
n = df_e #设置自由度n
alpha=0.05 #设置alpha
a=f.ppf(q=alpha, dfn=m, dfd=n) #单侧左分位点
b=f.isf(q=alpha, dfn=m, dfd=n) #单侧右分位点
print('单侧左、右分位点:a=%.4f, b=%.4f'%(a, b))
a1, b1=f.interval(1-alpha, dfn=m, dfd=n) #双侧分位点
print('双侧左、右分位点:a=%.4f, b=%.4f'%(a1, b1))
## 可以发现 MS_A/MS_e = 9.25 > Fm,n(0.05) = 5.7147 拒绝原假设H0,即存在组间差异
0.0065472957497462216
单侧左、右分位点:a=0.0516, b=4.2565
双侧左、右分位点:a=0.0254, b=5.7147
3. 方差分析公式及原理参考
SS_e: 随机误差的影响,又被称为组内偏差;
SS_A: 另一部分表示因素A的各水平之间的差异带来的影响,又被称为组间偏差。
原理参考:https://zhuanlan.zhihu.com/p/33357167 (方差分析的好文章)