哈希桶——开放定址法

news2024/10/7 5:27:35

哈希表的迭代器：

迭代器模板介绍：

template<class K, class T, class Ref, class Ptr, class KeyOfT, class Hash>

K:关键词类型

T:存储的数据类型

Ref:T& （operator*() 解引用函数的返回类型）

Ptr:T*      (operator->() 使用指针去操作成员)

KeyOfT:是外面哈希map （哈希map中存的是键值对 键值对的第一个数据就是key 第二个数据就是value 存储的数据） 和哈希set （哈希set中存的是value ）

外部会提供调函数去调用关键词key

Hash:是哈希函数将K关键词转化为hashi哈希桶的位置进行存储 将key转化为整数的函数 为了确定哈希桶的位置

哈希迭代器的成员介绍：

		Node* _node;
		const HashTable<K, T, KeyOfT, Hash>* _pht;

		size_t _hashi;

迭代器中_node 是实现 operator*(),operator->(),operator!=().

_hashi:每一次桶的位置 operator++()会运用到进行节点的遍历 记录每次桶的位置方便遍历

_pht:哈希表获取哈希桶的数据参数，获取哈希表的成员数据，成员函数等，我个人认为这个成员很方便也很重要 

哈希表的默认构造：

		__HTIterator(Node* node, HashTable<K, T, KeyOfT, Hash>* pht, size_t hashi)
			:_node(node)
			,_pht(pht)
			,_hashi(hashi)
		{}

		__HTIterator(Node* node, const HashTable<K, T, KeyOfT, Hash>* pht, size_t hashi)
			:_node(node)
			, _pht(pht)
			, _hashi(hashi)
		{}

利用初始化列表进行初始化，根据外面传的参数类型选择对应的默认构造函数，进行初始化构造。

哈希表迭代器中的操作符重载：

* -> !=

		Ref operator*()
		{
			return _node->_data;
		}

		Ptr operator->()
		{
			return &_node->_data;
		}

		bool operator!=(const Self& s)
		{
			return _node != s._node;
		}

 !=利用迭代器中存储的_node进行判断 判断是否为同一个指针。

* 对节点数据进行引用

-> 对节点数据地址进行返回 但是Ptr=T* (*和-> 相遇会抵消 所以也是数据)

++

		Self& operator++()
		{
			if (_node->_next)
			{
				// 当前桶还有节点，走到下一个节点
				_node = _node->_next;
			}
			else
			{
				// 当前桶已经走完了，找下一个桶开始
				//KeyOfT kot;
				//Hash hf;
				//size_t hashi = hf(kot(_node->_data)) % _pht._tables.size();
				++_hashi;
				while (_hashi < _pht->_tables.size())
				{
					if (_pht->_tables[_hashi])
					{
						_node = _pht->_tables[_hashi];
						break;
					}

					++_hashi;
				}

				if (_hashi == _pht->_tables.size())
				{
					_node = nullptr;
				}
			}

			return *this;
		}

 这里重点解释一下_node->_next为空之后的操作

1,第一个++hashi 为什么？

因为哈希表中的bigin() 会进行哈希桶的遍历 返回第一个不为空的哈希桶 （用该位置的节点，哈希表指针，哈希桶位置进行迭代器的赋值）但是begin()只会提供第一个不为空的哈希桶位置 不会将哈希桶进行向后遍历 如果该桶的单链表遍历完毕 到末尾nullptr 就应该找下一个通的位置 如果下一个桶的位置也为空 再向后找

第一个++hashi 就是单链表遍历完毕遇到空进行下一个哈希桶的查找
第二个++hashi 是该哈希桶位置本身为空 进行向后的查找

2.找到不为空的哈希表位置之后 再进单链表的迭代遍历

返回的就是迭代器*this

哈希表模板的介绍：

template<class K, class T, class KeyOfT, class Hash>

K:关键词类型

T:存储数据类型

KeyOfT:外部提取key所配的专用函数

Hash: 将key转化为整数的函数 为了确定哈希桶的位置

哈希表中的友元：

		template<class K, class T, class Ref, class Ptr, class KeyOfT, class Hash>
		friend struct __HTIterator;

由于哈希表迭代器成员中存在哈希表指针，二哈希表指针会访问哈希表成员，所以将哈希表迭代器设置为哈希表的友元。 

哈希表中类型的typedef

		typedef __HTIterator<K, T, T&, T*, KeyOfT, Hash> iterator;
		typedef __HTIterator<K, T, const T&, const T*, KeyOfT, Hash> const_iterator;

根据外部的调用进行对应的调用。const迭代器就调用const对应的迭代器。 

哈希表的节点：

	template<class T>
	struct HashNode
	{
		HashNode<T>* _next;
		T _data;

		HashNode(const T& data)
			:_data(data)
			,_next(nullptr)
		{}
	};

由于哈希桶是单链表构成的所以类节点的成员为该节点类型的指针 和数据 ，将节点初始化为空。

哈希表的查找：

		iterator Find(const K& key)
		{
			Hash hf;
			KeyOfT kot;

			size_t hashi = hf(key) % _tables.size();
			Node* cur = _tables[hashi];
			while (cur)
			{
				if (kot(cur->_data) == key)
				{
					return iterator(cur, this, hashi);
				}

				cur = cur->_next;
			}

			return end();
		}

这里就是简单的单链表遍历查找，利用哈希函数和KeyOfT外部函数进行关键词的查找，存在返回迭代器，不存在返回end(). 

哈希表的插入：

		pair<iterator, bool> Insert(const T& data)
		{
			Hash hf;
			KeyOfT kot;

			iterator it = Find(kot(data));
			if (it != end())
				return make_pair(it, false);

			// 负载因子最大到1
			if (_n == _tables.size())
			{
				vector<Node*> newTables;
				newTables.resize(_tables.size() * 2, nullptr);
				// 遍历旧表
				for (size_t i = 0; i < _tables.size(); i++)
				{
					Node* cur = _tables[i];
					while(cur)
					{
						Node* next = cur->_next;

						// 挪动到映射的新表
						size_t hashi = hf(kot(cur->_data)) % newTables.size();
						cur->_next = newTables[i];
						newTables[i] = cur;

						cur = next;
					}

					_tables[i] = nullptr;
				}

				_tables.swap(newTables);
			}

			size_t hashi = hf(kot(data)) % _tables.size();
			Node* newnode = new Node(data);

			// 头插
			newnode->_next = _tables[hashi];
			_tables[hashi] = newnode;
			++_n;

			return make_pair(iterator(newnode, this, hashi), true);
		}

首先判断该关键词是存在，如果存在就返回存在数据位置的迭代器和false;

 这里面的扩容是插入元素与哈希桶的数量相同就扩容，这里不是固定的，你可以判断每个哈希桶的大小最大不超过多少，再去扩容，这里方法很自由，没有固定的。

对于新表元素的插入，新表元素的插入方法与旧表类似，所以就可以直接赋用旧表的插入方法，这里很容易被看作递归，但不是递归，是代码赋用。

将新表插入完毕之后 再将旧表数据与新表数据进行交换，这里新表出了作用域就调用其对应的析构函数进行析构。大大的方便。

插入成功返回新节点位置的迭代器迭代器进行赋值（存在时的赋值在find函数中有涉及），和true.

哈希表的析构与构造：

		HashTable()
		{
			_tables.resize(10);
		}

		~HashTable()
		{
			for (size_t i = 0; i < _tables.size(); i++)
			{
				Node* cur = _tables[i];
				while (cur)
				{
					Node* next = cur->_next;
					delete cur;
					cur = next;
				}
				_tables[i] = nullptr;
			}
		}

哈希表的默认构造函数：对vector进行初始容量的 扩容；

哈希表的析构函数：从第一个桶位置开始进行遍历 跳过nullptr位置 将存在数据的位置进行单链表遍历删除 删除完单链表之后 再将该位置置为空。

哈希表的删除：

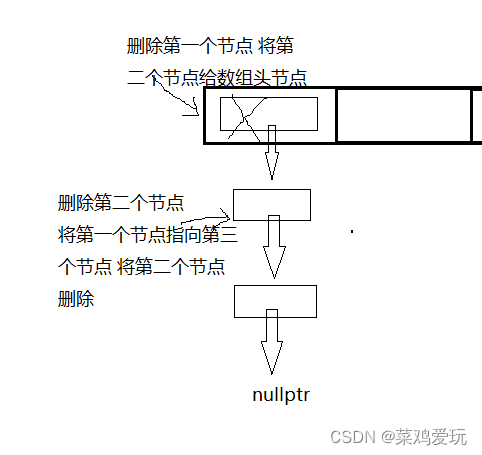
        哈希表节点的删除可以分为两种情况：

        第一种，删除哈希桶的头节点

        第二种，删除除头结点的任意节点

通过哈希函数将key转换为关键词，再遍历哈希桶（单链表）利用KeyOfT将数据进行提取找到要删除的数据 再进行上面两种情况的判断。

		bool Erase(const K& key)
		{
			Hash hf;
			KeyOfT kot;

			size_t hashi = hf(key) % _tables.size();
			Node* prev = nullptr;
			Node* cur = _tables[hashi];
			while (cur)
			{
				if (kot(cur->_data) == key)
				{
					if (prev == nullptr)
					{
						_tables[hashi] = cur->_next;
					}
					else
					{
						prev->_next = cur->_next;
					}
					delete cur;

					return true;
				}

				prev = cur;
				cur = cur->_next;
			}

			return false;
		}

哈希桶长度，数量，最大长度，平均桶长的统计： 

		void Some()
		{
			size_t bucketSize = 0;
			size_t maxBucketLen = 0;
			size_t sum = 0;
			double averageBucketLen = 0;

			for (size_t i = 0; i < _tables.size(); i++)
			{
				Node* cur = _tables[i];
				if (cur)
				{
					++bucketSize;
				}

				size_t bucketLen = 0;
				while (cur)
				{
					++bucketLen;
					cur = cur->_next;
				}

				sum += bucketLen;

				if (bucketLen > maxBucketLen)
				{
					maxBucketLen = bucketLen;
				}
			}

			averageBucketLen = (double)sum / (double)bucketSize;

			printf("all bucketSize:%d\n", _tables.size());
			printf("bucketSize:%d\n", bucketSize);
			printf("maxBucketLen:%d\n", maxBucketLen);
			printf("averageBucketLen:%lf\n\n", averageBucketLen);
		}

上面代码就是简单的遍历，不做过多讲解。

完整代码：

namespace hash_bucket
{
	template<class T>
	struct HashNode
	{
		HashNode<T>* _next;
		T _data;

		HashNode(const T& data)
			:_data(data)
			,_next(nullptr)
		{}
	};

	// 前置声明
	template<class K, class T, class KeyOfT, class Hash>
	class HashTable;

	template<class K, class T, class Ref, class Ptr, class KeyOfT, class Hash>
	struct __HTIterator
	{
		typedef HashNode<T> Node;
		typedef __HTIterator<K, T, Ref, Ptr, KeyOfT, Hash> Self;
		Node* _node;
		const HashTable<K, T, KeyOfT, Hash>* _pht;

		// vector<Node*> * _ptb;

		size_t _hashi;

		__HTIterator(Node* node, HashTable<K, T, KeyOfT, Hash>* pht, size_t hashi)
			:_node(node)
			,_pht(pht)
			,_hashi(hashi)
		{}

		__HTIterator(Node* node, const HashTable<K, T, KeyOfT, Hash>* pht, size_t hashi)
			:_node(node)
			, _pht(pht)
			, _hashi(hashi)
		{}

		Self& operator++()
		{
			if (_node->_next)
			{
				// 当前桶还有节点，走到下一个节点
				_node = _node->_next;
			}
			else
			{
				// 当前桶已经走完了，找下一个桶开始
				//KeyOfT kot;
				//Hash hf;
				//size_t hashi = hf(kot(_node->_data)) % _pht._tables.size();
				++_hashi;
				while (_hashi < _pht->_tables.size())
				{
					if (_pht->_tables[_hashi])
					{
						_node = _pht->_tables[_hashi];
						break;
					}

					++_hashi;
				}

				if (_hashi == _pht->_tables.size())
				{
					_node = nullptr;
				}
			}

			return *this;
		}

		Ref operator*()
		{
			return _node->_data;
		}

		Ptr operator->()
		{
			return &_node->_data;
		}

		bool operator!=(const Self& s)
		{
			return _node != s._node;
		}
	};

	// unordered_set -> Hashtable<K, K>
	// unordered_map -> Hashtable<K, pair<K, V>>
	template<class K, class T, class KeyOfT, class Hash>
	class HashTable
	{
		typedef HashNode<T> Node;

		template<class K, class T, class Ref, class Ptr, class KeyOfT, class Hash>
		friend struct __HTIterator;

	public:
		typedef __HTIterator<K, T, T&, T*, KeyOfT, Hash> iterator;
		typedef __HTIterator<K, T, const T&, const T*, KeyOfT, Hash> const_iterator;

		iterator begin()
		{
			for (size_t i = 0; i < _tables.size(); i++)
			{
				if (_tables[i])
				{
					return iterator(_tables[i], this, i);
				}
			}

			return end();
		}

		iterator end()
		{
			return iterator(nullptr, this, -1);
		}

		const_iterator begin() const
		{
			for (size_t i = 0; i < _tables.size(); i++)
			{
				if (_tables[i])
				{
					return const_iterator(_tables[i], this, i);
				}
			}

			return end();
		}

		// this-> const HashTable<K, T, KeyOfT, Hash>*
		const_iterator end() const
		{
			return const_iterator(nullptr, this, -1);
		}

		HashTable()
		{
			_tables.resize(10);
		}

		~HashTable()
		{
			for (size_t i = 0; i < _tables.size(); i++)
			{
				Node* cur = _tables[i];
				while (cur)
				{
					Node* next = cur->_next;
					delete cur;
					cur = next;
				}
				_tables[i] = nullptr;
			}
		}

		pair<iterator, bool> Insert(const T& data)
		{
			Hash hf;
			KeyOfT kot;

			iterator it = Find(kot(data));
			if (it != end())
				return make_pair(it, false);

			// 负载因子最大到1
			if (_n == _tables.size())
			{
				vector<Node*> newTables;
				newTables.resize(_tables.size() * 2, nullptr);
				// 遍历旧表
				for (size_t i = 0; i < _tables.size(); i++)
				{
					Node* cur = _tables[i];
					while(cur)
					{
						Node* next = cur->_next;

						// 挪动到映射的新表
						size_t hashi = hf(kot(cur->_data)) % newTables.size();
						cur->_next = newTables[i];
						newTables[i] = cur;

						cur = next;
					}

					_tables[i] = nullptr;
				}

				_tables.swap(newTables);
			}

			size_t hashi = hf(kot(data)) % _tables.size();
			Node* newnode = new Node(data);

			// 头插
			newnode->_next = _tables[hashi];
			_tables[hashi] = newnode;
			++_n;

			return make_pair(iterator(newnode, this, hashi), true);
		}

		iterator Find(const K& key)
		{
			Hash hf;
			KeyOfT kot;

			size_t hashi = hf(key) % _tables.size();
			Node* cur = _tables[hashi];
			while (cur)
			{
				if (kot(cur->_data) == key)
				{
					return iterator(cur, this, hashi);
				}

				cur = cur->_next;
			}

			return end();
		}

		bool Erase(const K& key)
		{
			Hash hf;
			KeyOfT kot;

			size_t hashi = hf(key) % _tables.size();
			Node* prev = nullptr;
			Node* cur = _tables[hashi];
			while (cur)
			{
				if (kot(cur->_data) == key)
				{
					if (prev == nullptr)
					{
						_tables[hashi] = cur->_next;
					}
					else
					{
						prev->_next = cur->_next;
					}
					delete cur;

					return true;
				}

				prev = cur;
				cur = cur->_next;
			}

			return false;
		}

		void Some()
		{
			size_t bucketSize = 0;
			size_t maxBucketLen = 0;
			size_t sum = 0;
			double averageBucketLen = 0;

			for (size_t i = 0; i < _tables.size(); i++)
			{
				Node* cur = _tables[i];
				if (cur)
				{
					++bucketSize;
				}

				size_t bucketLen = 0;
				while (cur)
				{
					++bucketLen;
					cur = cur->_next;
				}

				sum += bucketLen;

				if (bucketLen > maxBucketLen)
				{
					maxBucketLen = bucketLen;
				}
			}

			averageBucketLen = (double)sum / (double)bucketSize;

			printf("all bucketSize:%d\n", _tables.size());
			printf("bucketSize:%d\n", bucketSize);
			printf("maxBucketLen:%d\n", maxBucketLen);
			printf("averageBucketLen:%lf\n\n", averageBucketLen);
		}

	private:
		vector<Node*> _tables;
		size_t _n = 0;
	};
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1270821.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【LeetCode】每日一题 2023_11_30 确定两个字符串是否接近 （数组、排序、哈希/位运算、脑筋急转弯）

【LeetCode】每日一题 2023_11_30 确定两个字符串是否接近 （数组、排序、哈希/位运算、脑筋急转弯）

文章目录 刷题前唠嗑题目&#xff1a;确定两个字符串是否接近题目描述代码与解题思路 结语 刷题前唠嗑 LeetCode&#xff1f;启动&#xff01;&#xff01;&#xff01; 刷完今天&#xff0c;我的每日一题就坚持一个月啦&#xff0c;月度勋章要到手啦 今早很尴尬&#xff0c;…
阅读更多...
利用 LD_PRELOAD劫持动态链接库，绕过 disable_function

利用 LD_PRELOAD劫持动态链接库，绕过 disable_function

目录 LD_PRELOAD 简介 程序的链接 动态链接库的搜索路径搜索的先后顺序&#xff1a; 利用LD_PRELOAD 简单的劫持 执行id命令 反弹shell 引申至 PHP 绕过disable_function 方法1&#xff1a;使用蚁剑的扩展工具绕过disable_function 方法2&#xff1a;利用 mail 函数…
阅读更多...
Nginx实现（动静分离）

Nginx实现（动静分离）

动静分离应该是听的次数较多的性能优化方案&#xff0c;那先思考一个问题&#xff1a;「「为什么需要做动静分离呢&#xff1f;它带来的好处是什么&#xff1f;」」 其实这个问题也并不难回答&#xff0c;当你搞懂了网站的本质后&#xff0c;自然就理解了动静分离的重要性。先来…
阅读更多...
代理注册行业CRM系统：提升客户满意度，增加业绩

代理注册行业CRM系统：提升客户满意度，增加业绩

代理注册行业客户量大、合同繁多&#xff0c;传统的管理方式不再能够满足代理注册企业的管理需求。为了响应国家的数字化号召&#xff0c;很多代理注册企业开始使用CRM系统。下面就来说说&#xff0c;代理注册行业CRM系统有什么作用&#xff1f; 1、客户信息管理 代理注册行业…
阅读更多...
洗袜子的洗衣机哪款好？内衣洗衣机便宜好用的牌子

洗袜子的洗衣机哪款好？内衣洗衣机便宜好用的牌子

不得不说洗衣机的发明解放了我们的双手&#xff0c;而我们从小到大就有这个意识&#xff0c;贴身衣物不可以和普通的衣服一起丢进去洗衣机一起&#xff0c;而内衣裤上不仅有肉眼看见的污渍还有手上根本无法消灭的细菌&#xff0c;但是有一款专门可以将衣物上的细菌杀除的内衣洗…
阅读更多...
vue找依赖包的网址

vue找依赖包的网址

https://www.npmjs.com/ 浅收藏一下
阅读更多...
【网络奇遇之旅】：那年我与计算机网络的初相遇

【网络奇遇之旅】：那年我与计算机网络的初相遇

&#x1f3a5; 屿小夏 &#xff1a; 个人主页 &#x1f525;个人专栏 &#xff1a; 计算机网络 &#x1f304; 莫道桑榆晚&#xff0c;为霞尚满天&#xff01; 文章目录 一. 前言二. 计算机网络的定义三. 计算机网络的功能3.1 资源共享3.2 通信功能3.3 其他功能 四. 计算机网络…
阅读更多...
tomcat控制台中文信息显示乱码

tomcat控制台中文信息显示乱码

问题现象 我的tomcat版本是10.1版本。 在cmd下启动tomcat&#xff0c;会新打开控制台输出窗口&#xff1a; 控制台窗口输出的中文信息是乱码&#xff1a; 问题原因 产生这个问题的原因是&#xff1a;控制台窗口的编码和输出到控制台窗口的日志信息编码不一致。 查看tomc…
阅读更多...
知乎第三季度财报不及预期，股价今年已累计下跌26.4%

知乎第三季度财报不及预期，股价今年已累计下跌26.4%

来源&#xff1a;猛兽财经 作者&#xff1a;猛兽财经 知乎(ZH)报告称&#xff0c;其2023财年第三季度的收入同比增长了12.1%&#xff0c;至1.401亿美元&#xff0c;但未达到市场普遍预期的1.436亿美元&#xff0c;所以在财报后其股价出现了下跌。 第三季度知乎每股美国存托股票…
阅读更多...
如何写好开发信标题？推荐的营销邮件主题？

如何写好开发信标题？推荐的营销邮件主题？

打开率高的开发信标题有哪些&#xff1f;怎么写吸引人邮件标题&#xff1f; 开发信标题是您的邮件首次与受众接触的部分&#xff0c;因此&#xff0c;它必须引起他们的兴趣&#xff0c;激发他们打开邮件的欲望。蜂邮EDM将讨论如何写好开发信标题&#xff0c;以及一些成功的开发…
阅读更多...
深入解析进程

深入解析进程

在现代计算机系统中&#xff0c;进程是一个核心概念&#xff0c;它代表了程序的执行实例。通过并发执行多个进程&#xff0c;计算机能够提高效率和资源利用率。 1. 进程的概念 进程是指在计算机系统中正在执行的程序的实例。每个进程都有自己的地址空间、寄存器集合、堆栈和文…
阅读更多...
ANN人工神经网络：从基础认知到现实理解

ANN人工神经网络：从基础认知到现实理解

什么是神经网络&#xff1f; 神经网络的再认知 前面我们了解过&#xff0c;人工神经网络&#xff08;Artificial Neural Network&#xff0c;ANN&#xff09;是人类为了模仿人大脑的神经网络结构创建出来的一种计算机系统结构。但如果仔细深入到神经网络当中&#xff0c;会慢…
阅读更多...
springMVC实验（二）—调式工具APIFOX的使用

springMVC实验（二）—调式工具APIFOX的使用

【知识要点】 后端开发调试工具 前后端分离已经成为互联网类软件开发主流模式&#xff0c;没有前端操作的支持&#xff0c;如何调试后端程序的就是开发人员必须解决的问题。如&#xff1a;get类请求可以直接使用浏览器就能模拟测试&#xff0c;但是post、put等类型的请求&…
阅读更多...
open3d-点云及其操作

open3d-点云及其操作

open3d提供了一个专门用于点云的数据结构 PointCloud。 class PointCloud(Geometry3D):color # 颜色normals # 法向量points # 点云def __init__(self, *args, **kwargs):"""__init__(*args, **kwargs)Overloaded function.1. __init__(self: open3d.cpu.py…
阅读更多...
对某登录站点的JS前端逆向思路

对某登录站点的JS前端逆向思路

前言 js逆向一直没有相关了解&#xff0c;虽然目前渗透遇见的不是很多&#xff0c;大多数遇见的要么不加密&#xff0c;要么无法实现其加密流程&#xff0c;不过最近看到了一个较为简单的站点正好能够逆向出来&#xff0c;就做了简单记录。本文旨在介绍js逆向的一些基础思路&a…
阅读更多...
Antd可编辑表格初始数据为空，单元格不能编辑的解决办法

Antd可编辑表格初始数据为空，单元格不能编辑的解决办法

黑科技超简单: 给table表格增加行className rowClassName{() > editable-row} 然后设置可编辑表格的行样式 .editable-row:hover .editable-cell-value-wrap {border: 1px solid #d9d9d9;border-radius: 4px;padding: 4px 11px;}.editable-cell-value-wrap {padding: 5px…
阅读更多...
网络调试助手 连接Onenet 多协议接入平台 TCP透传协议

网络调试助手 连接Onenet 多协议接入平台 TCP透传协议

onenet文档链接 多协议接入地址 打开Onenet平台&#xff0c;多协议接入 选择TCP透传协议&#xff0c;点击添加产品&#xff0c;输入信息&#xff0c;点击确认 点击设备列表&#xff0c;添加设备 下面需要上传一个解析脚本文件该文件的下载地址lua文件下载地址 建立连接 设备…
阅读更多...
Vmware虚拟化引擎开启

Vmware虚拟化引擎开启

VMware虚拟化引擎开启可以优化虚拟机性能和安全性&#xff0c;但总会出现打开后报错的情况&#xff0c;需要按以下步骤设置处理。 通过任务管理器查看CPU是否已经启用虚拟化 在启用或关闭windows功能中去掉和虚拟化配置相关的功能项后重启 在VMware中选择需要的虚拟化引擎&…
阅读更多...
上海震坤行：水泥行业数字化采购的趋势、策略与实践

上海震坤行：水泥行业数字化采购的趋势、策略与实践

上海震坤行&#xff1a;水泥行业数字化采购的趋势、策略与实践 在中国水泥协会发布的《2023年上半年水泥行业经济运行及下半年展望》中提到了水泥行业的发展现状——2023年上半年&#xff0c;在全球经济增长放缓、国内经济延续恢复态势、但市场需求不足的宏观环境下&#xff0…
阅读更多...
Leetcode394. 字符串解码

Leetcode394. 字符串解码

Every day a Leetcode 题目来源&#xff1a;394. 字符串解码 解法1&#xff1a;栈 本题中可能出现括号嵌套的情况&#xff0c;比如 2[a2[bc]]&#xff0c;这种情况下我们可以先转化成 2[abcbc]&#xff0c;在转化成 abcbcabcbc。我们可以把字母、数字和括号看成是独立的 TO…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023