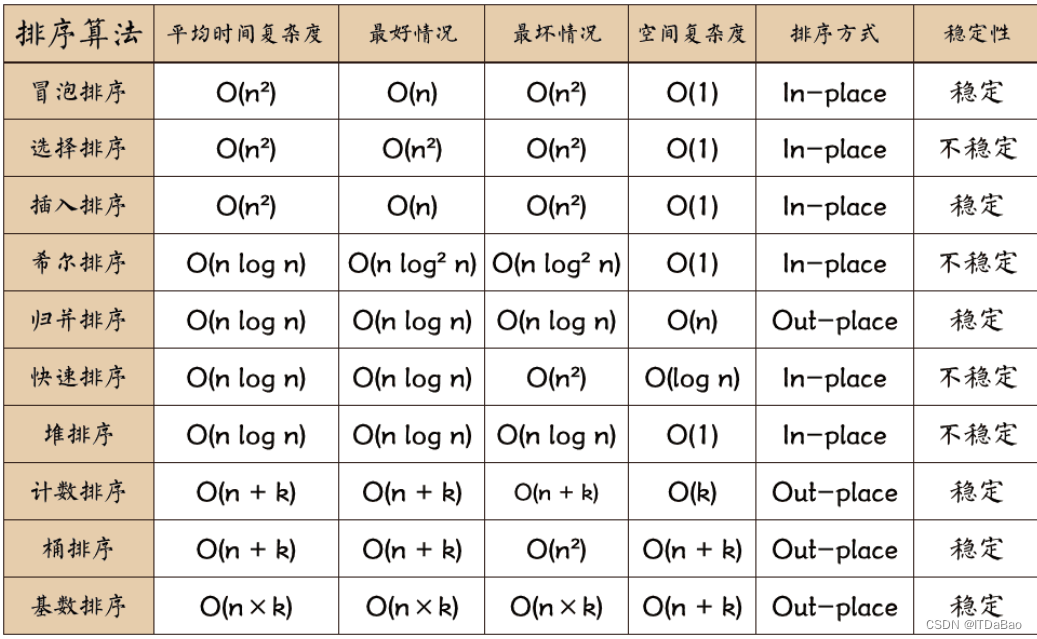
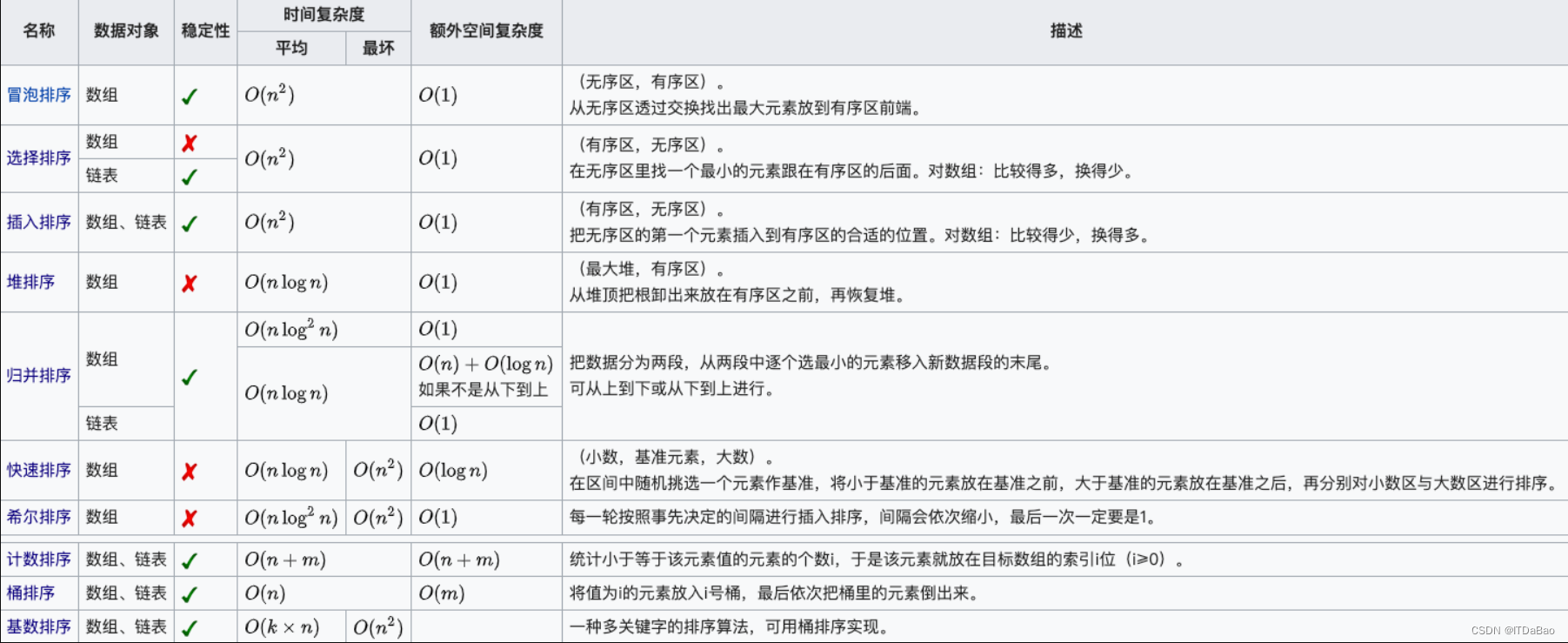
1.1 冒泡排序
public class BubbleSort {
public static void main(String[] args) {
int[] arr = {133,322,13,444,54,621,174,18,19,2};
System.out.println(Arrays.toString(arr));
BubSort(arr);
System.out.println(Arrays.toString(arr));
}
//冒泡排序
public static void BubSort(int[] arr){
//临时变量,存储较大元素
int temp;
//控制比较多少轮
for(int i=0;i<arr.length;i++)
{
//控制比较次数
for(int j=0;j<arr.length-1-i;j++)
{
if(arr[j]>arr[j+1]){
temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
}
}
}
}
}
1.2 快速排序
//快速排序
public static void QuiSort(int[] arr,int start,int end) {
if (start < end) {
//找到数组的标准数
int stard = arr[start];
//记录排序的下标
int low = start;
int high = end;
while (low < high) {
//如果右边数字大于标准数
while (low < high && stard <= arr[high]) {
high--;
}
//如果右边数字小于标准数,需要替换左边的数字
arr[low] = arr[high];
//如果左边数字小于标准数字
while (low < high && arr[low] <= stard) {
low++;
}
//如果右边数字大于标准数,需要替换右边的数字
arr[high] = arr[low];
}
//标准数赋值
arr[low] = stard;
//System.out.println("第一次排序"+Arrays.toString(arr));
//第一次已经排好,使用递归分开处理
//处理所有小的数字
QuiSort(arr, start, low);
//处理所有大的数字
QuiSort(arr, low+1, end);
}
}
}
1.3 插入排序
public static void insertSort(int [] arr){
//遍历所有数字:从后往前比较
// 从下标为1的元素开始选择合适的位置插入,因为下标为0的只有一个元素,默认是有序的
for(int i=1;i<arr.length;i++)
{
if(arr[i]<arr[i-1]){
int temp=arr[i];
int j;
//遍历当前数字前面所有数字,如果前面数字大于后面数字temp,交换
for(j=i-1;j>=0&&temp<arr[j];j--){
//把前一个数字赋给后一个数字
arr[j+1]=arr[j];
//方法二:
//arr[j]=temp;
}
//当比较到不小于temp的值:临时变量(外层for循环的当前元素)赋给不符合条件的后一个位置pos
//方法一:
arr[j+1]=temp;
}
}
}
1.4 希尔排序
public static void shellSort(int[] arr) {
int k=1;
//遍历所有步长
for (int d = arr.length / 2; d > 0; d /= 2) {
//遍历所有元素
for (int i = d; i < arr.length; i++) {
for (int j = i - d; j >= 0; j -= d) { //比较的元素是j=j-d; 1 3 5 7
//如果当前元素大于加上步长的元素(从小到大)
if (arr[j] > arr[j + d]) {
//交换元素
int temp = arr[j];
arr[j] = arr[j + d];
arr[j + d] = temp;
}
}
}
System.out.println("第" + k + "次排序后的数组" + Arrays.toString(arr));
k++;
}
}
1.5 选择排序
//选择排序
public static void selectSort(int[]arr){
//遍历所有数字
for(int i=0;i<arr.length;i++){
int minIndex=i;
//当前遍历的数和后面的数字依次比较,记录最小数字的下标
//寻找最小的元素下标
for(int j=i+1;j<arr.length;j++){
//如果后面比较的数比记录的最小数小
if(arr[minIndex]>arr[j]){
//记录最小数的下标
minIndex=j;
}
}
//如果最小的数和当前遍历数的下标不一样,说明后面下标为minIndex的数比当前遍历的数更小
//交换数字
if(i!=minIndex){
int temp=arr[i];
arr[i]=arr[minIndex];
arr[minIndex]=temp;
}
}
}
1.6 归并排序
public class MergeSort {
public static void main(String[] args) {
int[]arr=new int[]{1111,112,4,55,555,111,244,145};
int mid=arr.length/2;
mergeSort(arr,0,arr.length-1);
System.out.println(Arrays.toString(arr));
}
//归并排序:递归和合并
public static void mergeSort(int[] arr,int left,int right) {
int mid=(left+right)/2;
if(left<right){
//处理左边
mergeSort(arr,left,mid);
//处理右边
mergeSort(arr,mid+1,right);
//归并操作:
merge(arr,left,mid,right);
}
}
//合并的方法:
// a数组的的第i个 和b数组的第j个比较。 小的先进入
public static void merge(int[] arr,int left,int mid,int right) {
//用于存储归并后的临时数组
int []temp=new int[right-left+1];
//模拟分成两个数组:
// 记录第一个数组中需要遍历的下标,[left,mid]
int i=left;
//记录第二个数组中遍历的下标 ,[mid+1,right]
int j=mid+1;
//用于记录临时数组中存放下标
int index=0;
//遍历两个数组
while(i<=mid&&j<=right){
//第一个数组的数据更小
if(arr[i]<arr[j]){
//放入小数据到临时数组中
temp[index]=arr[i];
i++;
}else{
temp[index]=arr[j];
j++;
}
//放入元素后,index后移动
index++;
}
//处理多余数据:a数组或者b数组中剩下元素的情况
while(j<=right){
temp[index]=arr[j];
j++;
index++;
}
//将数组arr中从索引为l到索引为mid的元素复制到临时数组temp中
while (i<=mid){
temp[index]=arr[i];
i++;
index++;
}
//临时数组中的数据重新存入原数组
for(int k=0;k<temp.length;k++) {
//从pos=low开始放入排序后的元素
arr[left+k]=temp[k];
}
}
}
1.7 堆排序
先把数组中元素变为大顶堆(根节点大于子节点),再对大顶堆进行排序(取出大顶堆中的最上面元素,再对下面进行调整;对调整好的大顶堆再取出最上面的元素,一直重复)。
//堆排序:升序使用大顶堆
//降序使用小顶堆
//先把数组中元素变为大顶堆(根节点大于子节点),再对大顶堆进行排序
import java.util.Arrays;
import java.util.HashMap;
public class HeapSort {
public static void main(String[] args) {
int[]arr=new int[]{9,6,8,7,0,1,10,4,2};
heapSort(arr);
System.out.println(Arrays.toString(arr));
}
//对调整好的大顶堆进行排序:
// 取出大顶堆中的最上面元素,再对下面进行调整;对调整好的大顶堆再取出最上面的元素,一直重复
public static void heapSort(int []arr){
//开始位置是最后一个非叶子节点,即最后一个节点的父节点
int start=(arr.length-1)/2;
//结束为止,数据长度-1
//从最后一个非叶子节点从后往前进行调整
for(int i=start;i>=0;i--){
maxHeap(arr,arr.length,i);
}
//先把数组中的第0个和堆中的最后一个数字交换位置,再把前面的处理为大顶堆
for(int i=arr.length-1;i>0;i--){
int temp=arr[0];
arr[0]=arr[i];
arr[i]=temp;
maxHeap(arr,i,0);
}
}
//(1)大顶堆
public static void maxHeap(int []arr,int size,int index){
// 找到左孩子节点
int lNode=2*index+1;
//找到右孩子节点
int rNode=2*index+2;
int max=index;
//和两个子节点分别对比,找出最大的节点
if(lNode<size&&arr[lNode]>arr[max]){
max=lNode;
}
if(rNode<size&&arr[rNode]>arr[max]){
max=rNode;
}
//交换位置
if(max!=index){
int temp=arr[index];
arr[index]=arr[max];
arr[max]=temp;
//交换位置后,对交换后的堆进行调整
maxHeap(arr, size,max);
}
}
}