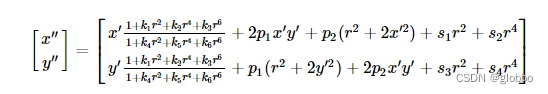《异常检测——从经典算法到深度学习》24 用于单变量时间序列异常检测的端到端基准套件

《异常检测——从经典算法到深度学习》

0 概论
1 基于隔离森林的异常检测算法
2 基于LOF的异常检测算法
3 基于One-Class SVM的异常检测算法
4 基于高斯概率密度异常检测算法
5 Opprentice——异常检测经典算法最终篇
6 基于重构概率的 VAE 异常检测
7 基于条件VAE异常检测
8 Donut: 基于 VAE 的 Web 应用周期性 KPI 无监督异常检测
9 异常检测资料汇总（持续更新&抛砖引玉）
10 Bagel: 基于条件 VAE 的鲁棒无监督KPI异常检测
11 ADS: 针对大量出现的KPI流快速部署异常检测模型
12 Buzz: 对复杂 KPI 基于VAE对抗训练的非监督异常检测
13 MAD: 基于GANs的时间序列数据多元异常检测
14 对于流数据基于 RRCF 的异常检测
15 通过无监督和主动学习进行实用的白盒异常检测
16 基于VAE和LOF的无监督KPI异常检测算法
17 基于 VAE-LSTM 混合模型的时间异常检测
18 USAD：多元时间序列的无监督异常检测
19 OmniAnomaly：基于随机循环网络的多元时间序列鲁棒异常检测
20 HotSpot：多维特征 Additive KPI 的异常定位
21 Anomaly Transformer: 基于关联差异的时间序列异常检测
22 Kontrast: 通过自监督对比学习识别软件变更中的错误
23 TimesNet: 用于常规时间序列分析的时间二维变化模型
24 TSB-UAD：用于单变量时间序列异常检测的端到端基准套件

24. TSB-UAD：一个用于单变量时间序列异常检测的端到端基准套件

论文名称：TSB-UAD: an end-to-end benchmark suite for univariate time-series anomaly detection
论文发表：Proceedings of the VLDB Endowment 2022
论文下载：https://www.paparrizos.org/papers/PaparrizosVLDB22a.pdf
源码下载：https://github.com/TheDatumOrg/TSB-UAD
数据集下载：Public: https://www.thedatum.org/datasets/TSB-UAD-Public.zip
Synthetic: https://www.thedatum.org/datasets/TSB-UAD-Synthetic.zip
Artificial: https://www.thedatum.org/datasets/TSB-UAD-Artificial.zip

24.1 论文概述

本篇论文概述了TSB-UAD，这是一个用于评估时间序列异常检测方法的全面基准套件，并分析影响这些方法性能的因素。论文介绍了时间序列异常检测的重要性，回顾了影响方法性能的因素，并提出了评估数据集难度的度量标准。此外，论文还对最近代表性方法在 TSB-UAD 上的初步实验评估进行了介绍，并总结了研究工作的意义。

与本系列提到的其他算法不同，本篇论文并没有提出一种核心算法，而是提出了一个全面的基准套件TSB-UAD，用于评估时间序列异常检测方法。论文还介绍了最近代表性方法在TSB-UAD上的初步实验评估，但并没有强调某种算法是核心算法。

回顾 2018 年举办的 “The 1st match for AIOps” 比赛 —— 一个典型的单指标时间序列异常检测比赛，比赛的中对不同算法的评估方法是计算带有 “报警延迟” 的方法，可以理解为 “准许的报警延迟时间”。从运维人员的角度来看，当故障发生后，7 个采样间隔时间内提示告警是允许的，超过 7 个采样间隔时间内的告警认为是无效的。

这个比赛中用到的评估方法是由赛事举办方制定的，应该也是根据运维人员的实际需求制定的，无可厚非。但实际上这种评估方法仅仅在部分领域（智能运维）有效。

本篇论文提出一种新的评估策略，具体内容不妨往后继续观看。谢谢各位的支持 ~

24.2 相关技术

这一部分介绍论文的第 3 个模块，也就是 BIASES IN TIME-SERIES AD EVALUATIONS。可以理解为相关背景、问题概述，作者在这里先抛出问题，下一个章节再介绍自己如何解决这些问题。换而言之，通过了解这几个关键问题，就知道作者这篇论文到底想解决哪些问题。

原论文中的 “RELETED WORK” 介绍的异常检测本系列博客介绍了很多次，而基准直接参考后面内容即可。

24.2.1 时间序列异常类型

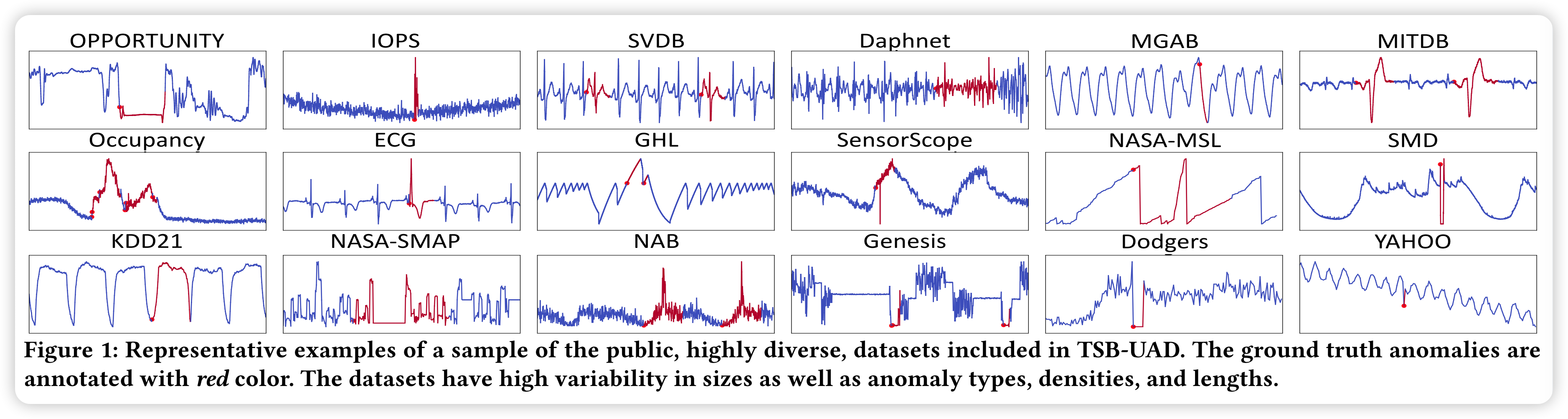
公共类别包含18个先前提出的1980年时间序列的数据集。图1 展示了数据集样本的典型示例及其明显的异常。可以看出来这些数据中的异常的特征大体上是不同的。数据集下载地址前面已经给出，感兴趣的小伙伴们可以前去下载。如果下载不了或者网速太慢请在下方留言邮箱，私发应该比网盘更快。
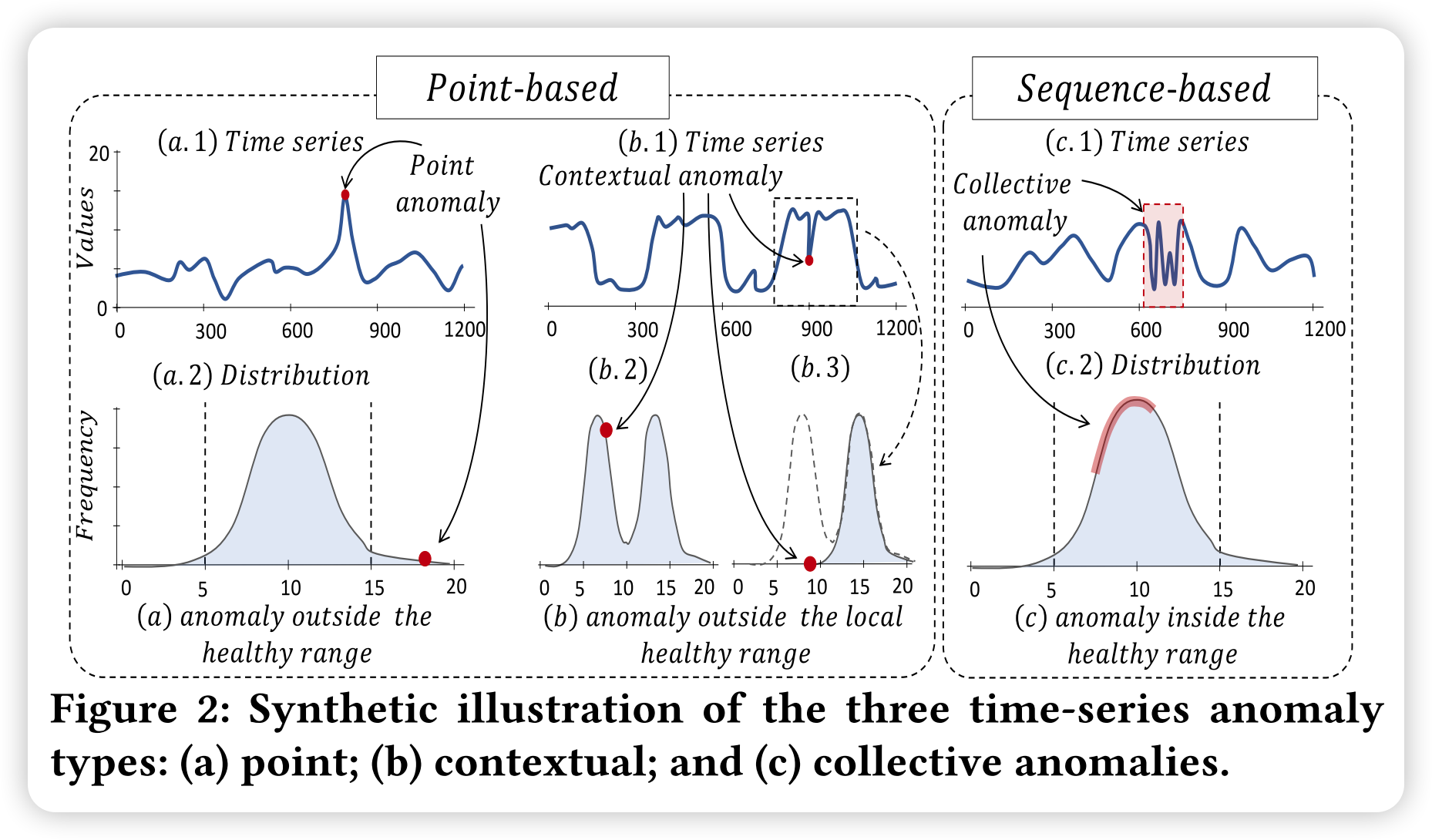
在这里插入图片描述
接着论文将这些异常进行了分类：point, contextual, and collective anomalies，即 点异常、上下文异常、以及集体异常。可以结合论文中的图2进行理解。

比如下图的 a 部分，即单个点的异常，两个例子分别表示时间序列中的值异常以及频率中，不符合分布模式的异常。

下图中的 b 部分，即上下文异常，两个例子中 b.1 相对于历史而言明显有个突降点，而 b.2 出现 “消失的尖峰” 现象，属于上下文异常。

图中的 c 部分，即集合异常，或者理解为时间片段异常，异常持续一段时间等。
在这里插入图片描述

24.2.2 数据集选择

数据集的选择依据即前面提到的异常类别。现在需要考虑的是这样选择数据集可能遇到的问题。将数据集排除在评估之外，会对之前定义的三种异常类型的不同算法进行一致的分析造成很大的障碍。例如，基于点的预测方法，通过比较预测与实际数据来检测异常，可能在Yahoo(有点异常)中表现良好，而在NAB(有集体异常)中表现较差。因此，只关注包含300多个时间序列的雅虎，可能看起来是一个广泛的评估，然而，由于基准的不完全性，该方法的评估是倾斜的。迫切需要评估自己提出的模型的新研究者和实践者(以及评估科学工作的评审者)，可能会忽略这一问题，并接受结果(例如，在300个时间序列中超越方法是重要的，即使一行代码的基线可以获得与复杂方法相当的结果)。重要的是，根据特定的应用程序或异常类别来证明数据集的选择是不现实的。例如，ECG数据可能主要包含集体异常(而不是单个点)。然而，并不能保证在现实环境中，用户故障或测量系统的不完善不能产生其他异常类型。

24.2.3 模型参数选择

本节内容抛出的问题是：为了尽可能合理地评估模型的效果，应当选择一组或多组合适的参数。那么如何选择模型的参数便成了一个非常关键的问题。

除了选择数据集来覆盖不同的异常类型外，同样重要的是数据集的内在特征，这影响了评估过程中模型参数的选择。在标准数据集中，一些数据集包含许多持续时间不同的异常和高异常污染 (如NASASMAP)，而另一些数据集 (如NAB) 则将异常限制在几个特定的持续时间内。其他数据集(例如，KDD21)将每个数据集的异常限制为一个，并使用单个索引而不是整个异常长度来评估模型。

异常格式的这种差异和数据集的特征使得调整必要的模型参数具有挑战性。作为例子，论文考虑现有方法报告异常的各种方法。具体来说，有些方法会返回每个点的原始异常分数，这要求操作者手动建立一个阈值来提取异常。其他方法通过调整阈值来简化这个过程。类似地，一些方法返回固定长度的异常，而另一些方法返回可变长度的异常。因此，仅调优与异常评分相关的参数就变得很麻烦。对于具有许多附加参数的方法(如深度学习方法)，参数选择过程变得混乱。通过分析几十篇论文及其代码库，可以明显地发现，在某些情况下，参数的调优不足或过拟合的情况。需要跨数据集进行评估的开放基准可以消除上述问题。

然而，参数的选择也可能为特定的方法提供不均衡的好处。例如，KDD21数据集可能包含多个异常，但它们的地面真实数据集中在大多数 “prominent” 异常。因此，设计提取单个异常的方法在这种环境下可能表现良好，但在异常污染严重的环境中，其性能可能会下降。类似地，提取所有异常但没有对其进行适当排序的方法可能会受到惩罚。为了评估方法的有效性和效率，特征的高度可变性是可取的。

24.2.4 评估指标选择

评估算法模型的好坏，当然也需要一个统一的量化标准。这个与语文作文、艺术创作不同。对算法的评估工作需要一个更加直观的、可量化的评估方法。

量化方法质量的测量方法的选择也可能对实验结果产生显著的偏差。各种各样的方法被用来评价异常检测方法。简单地说，传统的测量方法，如Precision, Recall和F-score，通过假设每个时间序列点可以标记为异常或不标记为异常(例如，通过一个异常分数的阈值)来评估方法。这些措施的缺点(即难以评估集体异常)促使了基于范围的变体的产生。因此，在使用传统度量方法时，选择具有集体异常的数据集可能会产生误导的结果。有趣的是，前面提到的度量方法需要设置一个阈值，以将点标记为异常或非异常。另一方面，AUC度量消除了这种需求，因为它的值独立于阈值。回到上面的kdd21例子，该例子包含多个异常，但ground truth中只有前1个出现，AUC的选择可以避免部分偏差，因为它避免了为提取单个异常而对异常分数设置阈值。

24.2.5 有限的可用数据集存在的缺陷

众所周知，带标签的数据是非常昂贵的，也正是这个原因，可用的数据是相当有限的。因此基于有限的数据对算法模型进行评估很容易存在偏差。这节描述的就是这个问题。

除了在选择数据集、参数和评估方法时产生的偏差，当前数据集的缺陷也可能导致误导性的结果。特别是，某些可用的时间序列异常检测数据集存在一些缺陷，导致人们批评的工作只关注它们的评价。

总而言之，对于一些数据集，一个简单的解决方案，简单地定义为一行代码 “baseline”，使用标准函数(例如，mean, std等)和一些调优的参数，可以实现最先进的性能。在其他情况下，数据集包含高密度的异常，可以对问题进行更多的分类。对于大多数异常出现在最后的数据集，它们可能提供了使预测偏向最后一点的机会。最后，错误的标记问题，即只有一些异常被标记出来，可能会导致假阳性和假阴性。

值得注意的是，一些数据集缺陷是有问题的，这主要是由于选择参数或评估措施方面的差异，如前所述。例如，一个简单的方法在所有这些 “trivial” 数据集上表现良好(不需要蛮力参数搜索)仍然是有价值的。换句话说，如果一种技术在一些更具挑战性的数据集上表现良好，那么在这样的 “trivial” 数据集上表现不好就令人担忧了。此外，如果评估的重点是大量的数据集(例如，预测最后一点异常的方法将不再适用于所有数据集)，那么高的异常密度或最后出现的异常将变得不那么重要。

然而，算法评估需要就准确(即没有错误标签)、多样化(即来自不同领域、具有不同的数据特征，包括不同类型的异常)以及适当测试相关算法的所有不同方面的基准达成一致。

24.3 核心方法

此模块关于原论文的第4部分进行介绍，即 TSB-UAD: BENCHMARK DETAILS 部分。此部分介绍 TSB-UAD 的具体内容，即前面提出的问题的解决方案。

这一部分原论文对收集到的数据集进行考察，做基本的分析；然后将时间序列分类数据集转换为带标注的异常检测数据集；接着对数据集进行划分，难度递增的合成数据集生成的数据转换；异常检测算法的评估方法与测试；以及最后评估异常检测数据集的难度。

24.3.1 数据集和基准测试套件

Datasets and Benchmarking Suite

TSB-UAD包括三个数据集类别，即公共数据集、人工数据集和合成数据集。公共数据集包含以前提出的出现在不同社区的文献中的数据集。人工数据集主要包括以前用于时间序列分类的真实数据集(超过90%)，并转换成带有标记异常的异常检测数据集。合成数据集是公共数据集的扩充版本，其中各种数据转换注入新的异常或增加其复杂性。

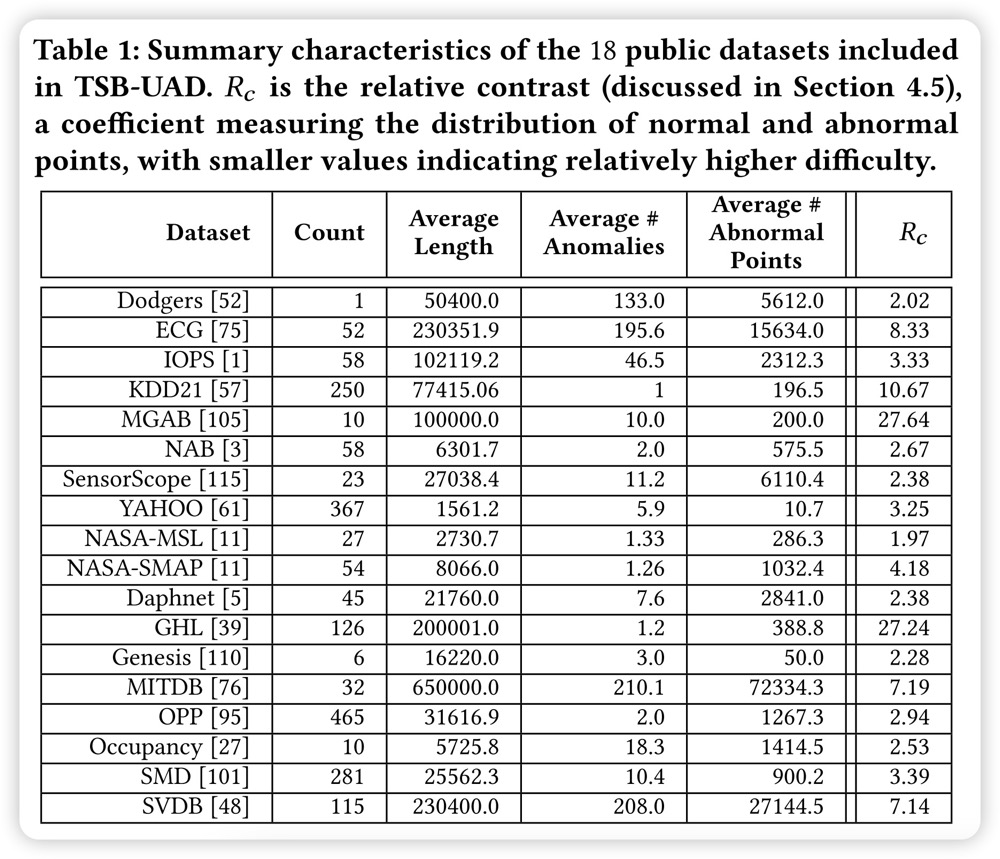
公共数据集：TSB-UAD包括三个数据集类别，即公共数据集、人工数据集和合成数据集。公共数据集包含以前提出的出现在不同社区的文献中的数据集。人工数据集主要包括以前用于时间序列分类的真实数据集(超过90%)，并转换成带有标记异常的异常检测数据集。合成数据集是公共数据集的扩充版本，其中各种数据转换注入新的异常或增加其复杂性。公共数据集：论文收集了过去几十年文献中提出的包含1980年标记异常的时间序列的18个数据集。具体来说，每个时间序列中的每个点都被标记为正常或异常。表1总结了数据集的相关特征，包括它们的大小和长度，以及关于异常的统计数据。前8个数据集最初包含单变量时间序列，而剩下的10个数据集最初包含多变量时间序列，论文将其转换为单变量时间序列。具体来说，分别在每个维度上运行论文中提到的异常检测方法，并且保留那些至少有一个方法实现 $\text{AUC} > 0.8$ 的维度。
在这里插入图片描述
人工数据集：为了利用现有的用于替代时间序列任务的真实数据集，参照现有的工作，从通用分类数据集系统地构建异常检测数据集。论文提出了一个适用于时间序列的版本，它将类标签分为正常和异常。这个过程生成了958个时间序列，属于126个数据集，对应于UCR Archive的数据集。尽管这是人工生成的过程，但这些时间序列主要对应于真实世界的数据集和应用程序(超过90%)。

合成数据集：考虑到开发异常合成时间序列的大量工作，论文研究并提出了一组全局、局部和子数据转换，目的是注入新的异常或增加识别现有异常的复杂性(见第4.3节)。本论文将这些转换应用于公共数据集，生成了92个增强数据集，其中包含10828个时间序列。重要的是，本论文提供了相应的脚本来帮助创建具有不同难度的指数级大型数据集，以评估时间序列异常检测方法。

TSB-UAD基准测试套件：请参考论文提供的源码，通过处理预处理和后处理步骤来隐藏基准测试异常检测方法的所有复杂性，例如数据加载、处理、生成和转换、模型评估和严格的统计分析。研究人员和实践者应该把注意力主要放在实现探测器上，即提取异常的方法。在论文的存储库中，提供了12个用于评估的监督和非监督检测器的示例。论文还跨所有类别发布所有数据集，以实现重现性目的，并在附带库之外使用。本部分内容我会在后面的实验中介绍。

24.3.2 将时间序列分类数据集转换为标注异常检测数据集

Transforming Time-Series Classification Datasets into Labeled AD Datasets

前面提到有限的可用数据数据集问题，需要一种有原则的方法来利用现有的时间序列分类数据集，将分配给每个时间序列的类标签转换为正常和异常。考虑到创建此类分类数据集背后几十年的努力，这是非常重要的。如果能够区分正常类和异常类，可以通过对正常类的时间序列进行采样(并串联)，同时控制异常类的采样时间序列注入时的异常密度来生成时间序列异常检测数据集。

一个关键的挑战是避免创建一个微不足道或不可能检测到异常的时间序列。为了实现目标，分为两个步骤: (1) 识别由 oracle 分类器给出的具有高度混淆的类对; (2) 对于选定的类对，生成时间序列，但只保留至少有一个检测器可以识别异常的情况。通过使用不同的阈值来评估检测精度，生成不同难度的数据集。对于TSB-UAD，利用SBD距离构造时间序列的不相似矩阵。SBD是一种快速、准确、无参数的距离测量方法，已经达到了最先进的性能。然后应用一个 1-NN (Nearest Neighbor) 分类器，使用预先计算的距离矩阵，并预测每个序列的标签。尽管存在更精确的分类器，但倾向于确定性和无参数的分类器，以确保结果的可重现性。

序列 $x$ 的标签 $y = j$ 被预测为 $\hat{y}=k$ 的概率，记作 $P(\hat{y}=k|x)$ 定义为从标签 $j$ 到标签 $k$ 的混淆因子。标签 $j$ 到 $k$ 的标准相似度为 $c_{jk} + c_{kj}) / 2$ 。论文构造所有 $m$ 标签之间的亲和矩阵，并根据这个矩阵计算最大生成树(MST)。或者，有人可能会考虑从最混乱的单个类中选择正常类和异常类。不幸的是，这将导致非常难以区分的情况。相反，MST步骤有助于构造具有最大总体亲和力的集。最后，将MST中相邻的节点用两种颜色表示，并指定一种颜色为正常颜色，另一种颜色为异常颜色。生成数据需要两个参数：异常段数 $K$ 和异常子序列比 $r$ 。正常段数为 $N = K / r - K$ 。假设异常集包含 $m$ 标签和 $n$ 数据。选择 $K$ 数据，而不是 $n$ 数据。如果 $n < K$ ，则取所有 $n$ 数据。计算最频繁的异常标签的频率 $f_a$ ，然后每个正常标签的频率 $f_n= 20 f_a$ 。选中的普通标签个数为 $L=N / f_n$ 。选取 $L$ 个法线标签，每个法线标签被选取 $f_n$ 次并进行替换。最后，将 $K$ 个异常段和 $N$ 个正常段进行打乱和拼接，形成一个合成时间序列。

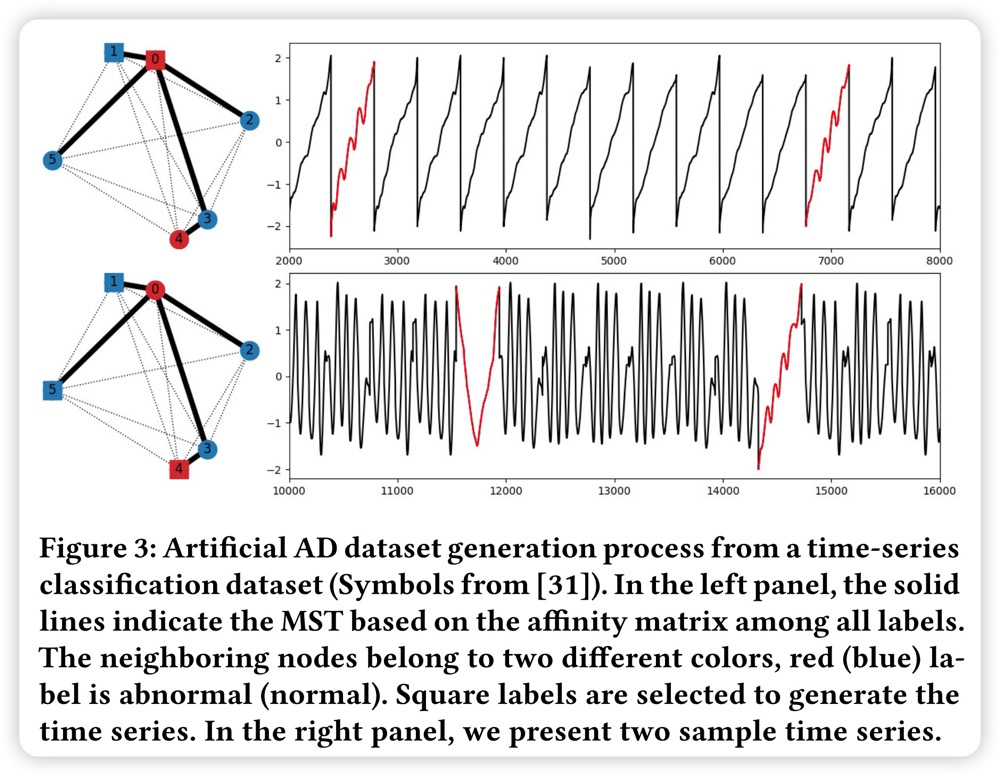
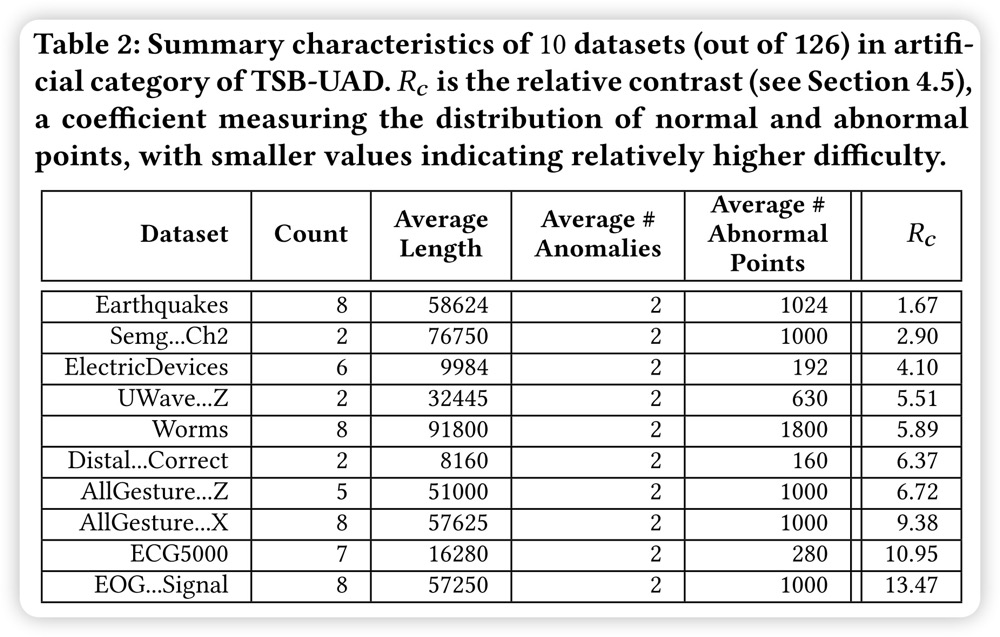
论文在UCR归档中的所有128个数据集上使用这个过程(在修复了不同长度和缺失值的问题之后)，每个数据集生成一个或多个时间序列。只保留在公共数据集中表现良好的五种无监督方法中至少有一种达到AUC高于0.65的时间序列。该过程完全排除了两个数据集和每个数据集生成的几个时间序列，得到126个数据集，958个时间序列。图3 显示了符号数据集的MST和相应的时间序列，以及注入的异常(红色部分)。表2 总结了TSB-UAD人工分类中10个代表性数据集的相关特征。

在这里插入图片描述

24.3.3 难度递增的合成数据集生成的数据转换

Data Transformations for Synthetic Dataset Generation of Increasing Difficulty

为了模拟额外的异常或增加异常检测的复杂性，论文研究了一组全局、局部和子序列转换。全局变换改变整个时间序列的特征，而局部和子序列变换改变时间序列的连续部分，将原始时间序列表示为 $X=(x_0,x_1,…,x_n)$ ，其标准差为 $s$ 。

全局变换：论文考虑了五种全局变换来改变时间序列，使用随机游走背景，白色噪声，点离群值，平滑和平滑段。具体地说，论文将随机游走定义为随机游走背景的强度（the strength of a random walk background）。

假设 $[- 1 ， 0 ， 1]$ 中的独立随机变量 $Z_i, i\in [1, n]$ ，并设置 $b_0 = 0$ 和 $b_n=\sum_{i=1}^n Z_i$ 。论文对原始时间序列进行如下变换： $x_i^{\prime}=x_i+p_{r w} \cdot s \cdot b_i$ 。同样，论文定义 $p_{wn}$ 为白噪声的强度 $b_i ~ \mathcal{N}(0,1), i\in [0,n]$ 。并对原始时间序列进行如下变换： $x_i^{\prime}=x_i+p_{r w} \cdot s \cdot b_i$ 。集成的背景不会改变每个点的标签，但对于某些方法，它们增加了异常检测的难度。对于点离群点，定义离群点比率 $p_{or}$ ，并从时间序列中随机选取 $\cdot p_{or}$ 个点。选择的数据点更改如下： $x_i^{\prime}=x_i + 5s$ 。另一个版本用原始时间序列的最大值替换所选数据： $x^{\prime}_i=\max{(X)}$ 。因此，点离群值可能会导致全局或上下文异常。对于平滑， $f$ 是一个线宽为 $p_{sm}$ 的高斯过滤器。平滑后的时间序列是原始时间序列 $X$ 和滤波 $f$ 之间的卷积，可以通过它们的傅立叶变换的乘积 $X^{\prime}=X*f=\mathcal{F}^{-1}*(\mathcal{F}(X)\mathcal{F}(f))$ 来计算。最后，通过改变具有不同平滑窗口的两个分段，将这一思想扩展到多个分段。将具有不同线宽 $p_1$ , $p_2$ 的两个高斯滤波器分别应用于时间序列的前半部分和后半部分，并将它们连接在一起 $X^{\prime}=[X_{0:n/2} * f_{p_1}, X_{n/2:n+1}*\mathcal{f_{p_2}}]$ 。

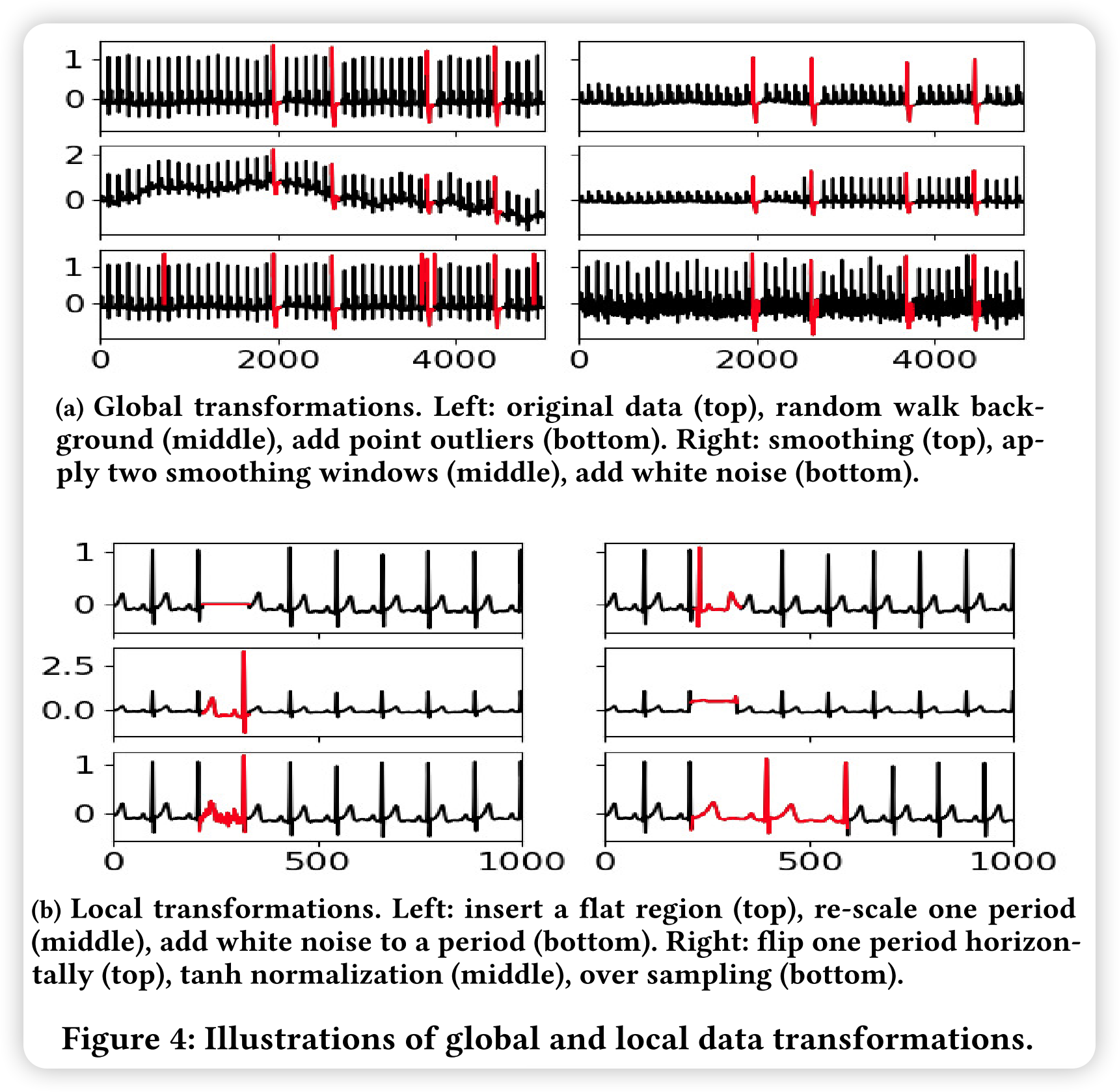
局部变换：论文呢考虑两个局部变换，旨在模仿集体异常。模式相关变换插入一个平台区域;水平翻转一个片段；用系数k重新缩放或移动一个片段；用k-score、MinMax、MedianNorm、MeanNorm、Logistic和Tanh标准化一个片段；或向一个片段添加白色噪声。频率相关的变换用新的频率重新采样片段。与点异常值比率类似，也可以定义转换周期比率，并将这些局部转换应用于所有选定的周期。图 4 显示了几个全局和局部数据转换应用于样本时间序列时的效果。
在这里插入图片描述
子序列变换：第三种类型的转换仅限于合成数据集。给定设置正常和异常序列，控制异常子序列比率、异常数据之间的亲和度以及异常和正常数据之间的亲和度。例如，图3 显示了基于同一数据集的两个合成时间序列。当选择标签 1 作为异常数据，标签 0 作为正常数据（上图）时，这两个异常数据是相似的，因为它们属于同一个标签。正常和异常的双折射率也是相似的。当选择标签 1 和 5 作为异常数据，标签 4 作为正常数据（下图）时，两个异常重复之间的距离以及异常重复和正常重复之间的距离都很明显。为了生成示例，遵循前面讨论的方法，首先对类进行着色（标记），然后从不同的颜色中随机选择类。集成的数据将包含各种级别的亲和力和虚假异常（通过黑盒异常检测方法过滤）。

TSB-UAD 中的初始转换捕获了整个选项范围的一部分。并且论文计划在不久的将来引入更高级的转换，例如马尔可夫转换模型或变参数模型。

24.3.4 异常检测的评价方法和测试

已经提出了几种措施来量化异常检测方法的质量。接下来论文回顾了这些措施，并提出一些缺点。TSB-UAD包括完整性的所有措施。

精确度 Precision、召回率 Recall 和 F-score： 略。

AUC: 略。

Range-Precision and Range-Recall 距离查准率和距离查全率： 为了减轻传统的查准率和查全率度量的缺点，它们的定义最近被扩展到捕获范围。具体地说，它们的定义考虑了几个因素：检测到的异常异常序列的数目与异常序列的总数的比率，检测到的点离群值的数目与点离群值的总数的比率，每个异常子序列中真阳性部分的相对位置，对应于一个真实的异常子序列的片段化预测区域的数目。如前所述，范围-F分数是范围-精确度和范围-召回率的调和平均值。

Precision@k： 最后，给定异常点的数量，另一种测量期望具有最显著异常分数的点为异常。 $k$ 通过将对应的 $TP$ 表示为 $TP @ k$ ，则 $P rec i s i o n @ k = TP @ k / k$ 。

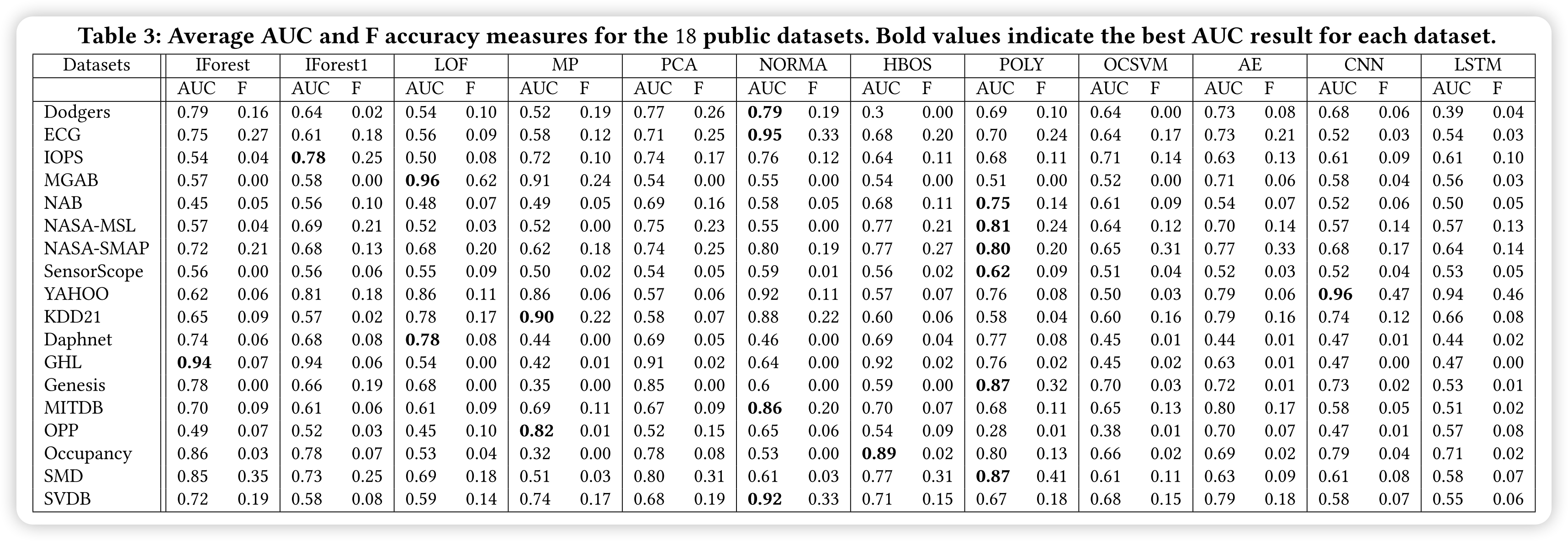
如前所述，TSB-UAD报告了所有措施，以全面了解每种方法。在论文的实验中，评估了所有测量对几个因素的灵敏度（第6.1节），并且由于AUC对噪声和正常/异常比率的鲁棒性，使用 AUC。重要的是，AUC 还避免了在设置阈值参数时所有其他测量对异常分数的依赖性。此外，TSB-UAD是一个模块化基准，可以集成新的测量（例如，范围-AUC和基于VUS的测量[86]）。
在这里插入图片描述
Statistical Analysis 统计分析： 考虑到在不同的数据集上进行评估，有必要进行适当的统计检验，以评估准确性差异的显著性。对于TSB-UAD，论文采用两种非参数统计检验：一种用于验证成对比较，另一种用于同时验证多种方法。具体来说，在文献 [32] 之后，使用Wilcoxon 检验来评估多个数据集上的方法对。为了在多个数据集上推理多种方法，论文使用 Friedman 检验，然后是事后 Nemenyi 检验。

24.3.5 评估异常检测数据集的难度

除了评估方法外，论文还考虑了评估异常检测时间序列难度的因素。为了说明这一点，图5显示了分为两个块的合成时间序列。在第一个方框中，图5（a）描述了一个只有一个异常的时间序列，图5（b.1）描述了一个有两个不同异常的时间序列，图5（b.2）描述了一个有两个相似（形状）异常的时间序列。在第二个块中，图5（c）描述了一个具有单一正态性的时间序列，图5（d）显示了一个具有两个不同正态性的时间序列。基于这两个案例，论文总结了影响异常检测的几个因素：（1）正态子序列的变化：具有单个或多个正态模式的时间序列（见图5（c）与（d））;（2）异常的变化：具有单一类型异常或多个不同异常的时间序列（见图5（a）与（b.1））;（3）异常的基数：时间序列包含唯一或多个相似的异常（见图5（b.1）与（b.2））。
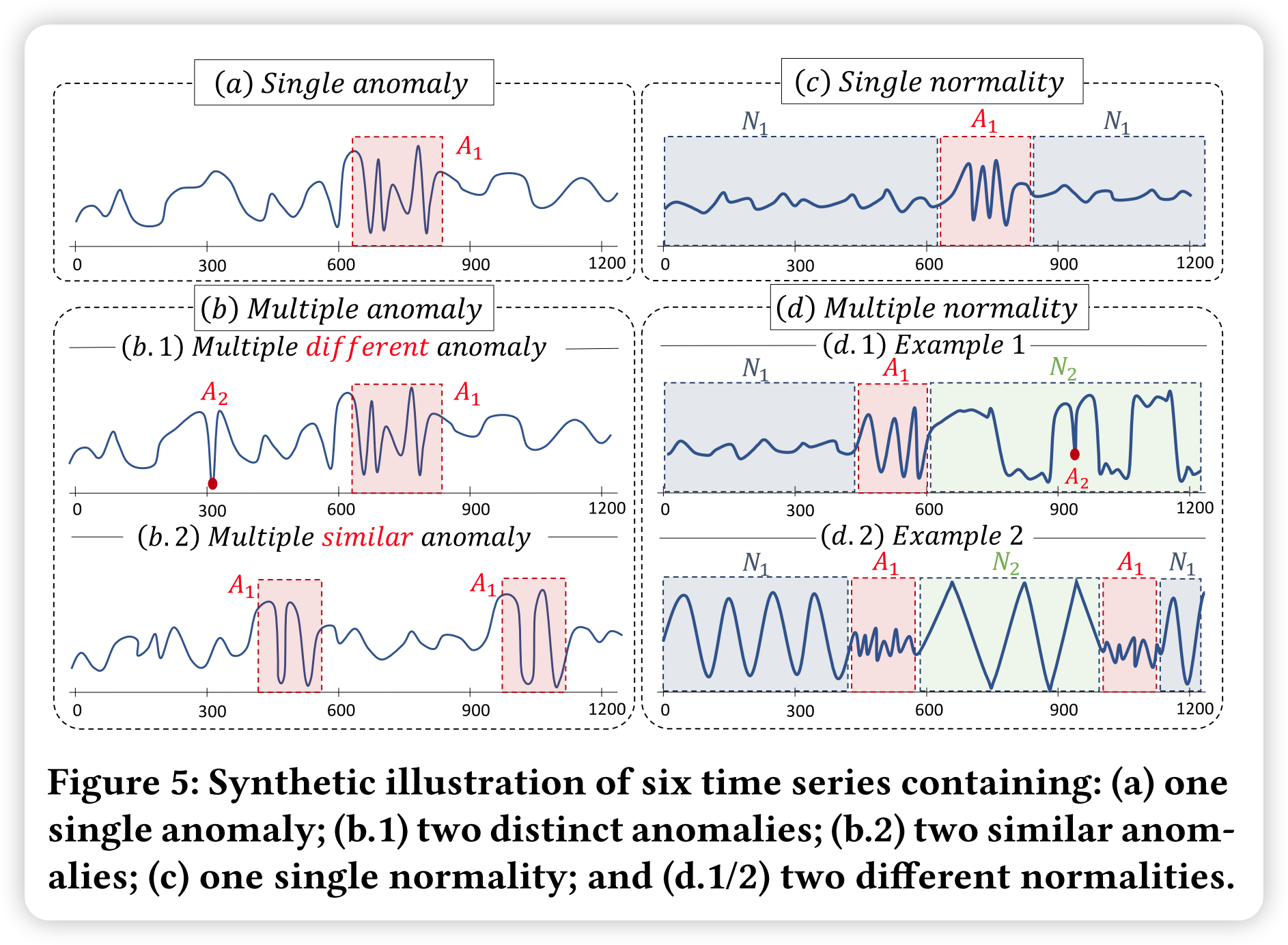
在这里插入图片描述

正如接下来将看到的，这些因素的不同组合可能会导致不同的适当方法进行异常检测。先前已经讨论了几个系数来捕获正常和异常点的分布。论文将这些定义推广到时间序列，并提出了一个适合于合成数据集的度量。

Relative Contrast (RC)：RC定义为所有数据点的平均距离期望值与最近邻距离期望值的比值。将两个序列 $s_i$ 和 $s_j$ 之间的 SBD 距离表示为 $D(s_i, s_j)$ ，整个集合为 $S$ 。对于每一个序列 $x$ ，它的 1-NN 距离 $D_{min}(x)=\min_{s\in {S-x}}D(x,s)$ 和平均距离 $D_{mean}(x)=\mathbb{E}_{s\in {S-x}}D(x,s)$ 。则相对对比度（relative contrast）为：

$R_c=\frac{\mathbb{E}_{s \in S}\left[D_{\text {mean }}(s)\right]}{\mathbb{E}_{s \in S}\left[D_{\text {min }}(s)\right]} .$

为了计算 RC，论文首先将时间序列按其周期进行分裂，并根据每对连续性之间的SBD距离构建距离矩阵。RC度量一个点的最近邻与其他点的可分性。如果RC更接近1，则平均距离接近最近邻距离，这表明数据分布均匀，聚类更困难。

Normalized clusteredness of abnormal points (NC)：NC是正常双稳态的平均 SBD 与异常双稳态的平均 SBD 的比值。表示正常序列的集合 $S_{nor}$ 和异常序列的集合 $S_{ano}$ ，则

$N_a=\frac{\min _{c_i \in C_{a n o}, c_j \in C_{\text {nor }}} D\left(c_i, c_j\right)}{\mathbb{E}_{c_i, c_j \in C_{n o r}, i \neq j}\left[D\left(c_i, c_j\right)\right]}$

如果系统只有一个正常群集，则NA为空。NA越大，表示异常点距离正常点越远。

RC是对整个数据集的聚类性的一般描述，NC是正常数据点和异常数据点之间的聚类性对比。NC和NA需要了解实际的正常和异常序列及其聚类，因此只能在合成数据集上计算。

24.4 论文实验

24.4.1 下载数据集

数据集下载地址本文前面已经给出，可以考虑使用迅雷等下载工具进行下载，并没有特别需要介绍的部分。

24.4.2 快速实验

首先将源码下载下来，并根据 requirement.txt 安装依赖，即

$ pip install -r requirements.txt

接着将 TSB_UAD 安装到本地，即

$ pip install .

接着查看实验部分，这部分内容源码仓库已经给出教程，这里也不再重复，大概介绍一下：

import os
import pandas as pd
from TSB_UAD.core import tsb_uad

# 读取csv文件
df = pd.read_csv('data/benchmark/ECG/MBA_ECG805_data.out', header=None).to_numpy()
# 拆分为数据与标签两部分
data = df[:, 0].astype(float)
label = df[:, 1]
# 使用套件进行评估，这里只是以 IForest 算法为例，其他算法类似地更改字符穿 'IForest' 
results = tsb_uad(data, label, 'IForest', metric='all')
# 输出评估结果
metrics = {}
for metric in results.keys():
    metrics[metric] = [results[metric]]
    print(metric, ':', results[metric])
# 导出评估结果
df = pd.DataFrame(data=metrics)
df.to_csv(os.path.join('./all_metrics.csv'))

24.5 速读源码

24.5.1 重点源码 TSB_UAD / transformer / transformer.py

def add_random_walk_trend(data, label, seed=5, p_walk=0.2):
    """
    向时间序列数据添加随机行走趋势。

    参数:
    - data (numpy数组): 时间序列数据。
    - label (numpy数组): 二进制标签，指示异常点（1）和正常点（0）。
    - seed (整数): 随机数生成的种子，用于可重复性。
    - p_walk (浮点数): 控制随机行走强度的参数。

    返回:
    - numpy数组: 转换后的时间序列数据。
    - numpy数组: 转换后的标签。
    """
    np.random.seed(seed)  # 设置随机种子以保证可重复性
    dims = 1  # 随机行走的维度（在这里是1维）
    step_n = len(data) - 1  # 随机行走的步数
    step_set = [-1, 0, 1]  # 可能的步幅集合
    origin = np.zeros((1, dims))  # 随机行走的初始位置

    # 在1维上模拟随机步幅
    step_shape = (step_n, dims)
    steps = np.random.choice(a=step_set, size=step_shape)  # 生成随机步幅
    trend = np.concatenate([origin, steps]).cumsum(0)  # 累积和得到随机行走趋势

    # 将随机行走趋势添加到原始数据中，乘以标准差和参数p_walk进行缩放
    return np.ravel(trend) * np.std(data) * p_walk + data, label

def add_white_noise(data, label, seed=5, p_whitenoise=0.2):
    """
    向时间序列数据添加白噪声。

    参数:
    - data (numpy数组): 时间序列数据。
    - label (numpy数组): 二进制标签，指示异常点（1）和正常点（0）。
    - seed (整数): 随机数生成的种子，用于可重复性。
    - p_whitenoise (浮点数): 控制白噪声强度的参数。

    返回:
    - numpy数组: 转换后的时间序列数据。
    - numpy数组: 转换后的标签。
    """
    np.random.seed(int(seed))  # 设置随机种子以保证可重复性
    return data + np.random.normal(size=len(data)) * np.std(data) * p_whitenoise, label
    

def filter_fft(data, label, p=21):
    """
    将数据转换为频域并过滤高频分量。

    参数:
    - data (numpy数组): 时间序列数据。
    - label (numpy数组): 二进制标签，指示异常点（1）和正常点（0）。
    - p (整数): 高斯滤波器的参数，控制滤波器宽度。

    返回:
    - numpy数组: 转换后的时间序列数据。
    - numpy数组: 转换后的标签。
    """
    n = len(data)
    
    t = np.linspace(-3, 3, p)  # 生成时间轴
    g = np.exp(-t**2)  # 生成高斯滤波器

    g_padded = np.hstack((g, np.zeros(n - p)))  # 对滤波器进行零填充
    
    # 信号的傅里叶变换
    xhat = np.fft.fft(data)
    
    # 滤波器的傅里叶变换
    ghat = np.fft.fft(g_padded)
    
    # 在傅里叶空间中应用滤波器
    tmp = xhat * ghat  
    
    # 转换回时域
    return np.real(np.fft.ifft(tmp)) / np.sum(g), label

def two_seg_freq_filter(data, label, p1=21, p2=51):
    """
    将数据分为两部分，分别应用两个不同的高斯滤波器，然后将它们合并。

    参数:
    - data (numpy数组): 时间序列数据。
    - label (numpy数组): 二进制标签，指示异常点（1）和正常点（0）。
    - p1 (整数): 第一个高斯滤波器的参数，控制第一个滤波器的宽度。
    - p2 (整数): 第二个高斯滤波器的参数，控制第二个滤波器的宽度。

    返回:
    - numpy数组: 转换后的时间序列数据。
    - numpy数组: 转换后的标签。
    """
    l0 = len(data) // 2  # 将数据分成两半
    data1 = data[:l0].copy()
    data2 = data[l0:].copy()

    # 对两部分数据分别应用不同的高斯滤波器
    data1_new, label1 = filter_fft(data1, label[:l0], p=p1)
    data2_new, label2 = filter_fft(data2, label[l0:], p=p2)

    # 将两部分数据合并
    return np.concatenate((data1_new, data2_new)), label


def select_region(length, contamination, period, seed):
    """
    给定总长度，生成将被转换的时间段。

    参数:
    - length (整数): 时间序列的总长度。
    - contamination (浮点数): 污染比例，表示需要转换的时间段占总长度的比例。
    - period (整数): 最小时间段的长度。
    - seed (整数): 随机数生成的种子，用于可重复性。

    返回:
    - 列表: 包含转换时间段的列表，每个时间段由起始点和结束点表示。
    """
    np.random.seed(int(seed))

    n = int(length * contamination)
    period = max(period, 10)

    m = int(n / period)

    region = []

    for i in range(m):
        s = int(length / m) * i
        e = int(length / m) * (i + 1)
        r = np.random.choice(np.arange(s, e - period), size=1)
        region.append([int(r), int(r + period)])

    return region

def add_point_outlier(data, label, seed=5, outlierRatio=0.01):
    """
    向时间序列数据添加离群点。

    参数:
    - data (numpy数组): 时间序列数据。
    - label (numpy数组): 二进制标签，指示异常点（1）和正常点（0）。
    - seed (整数): 随机数生成的种子，用于可重复性。
    - outlierRatio (浮点数): 离群点的比例，表示需要添加的离群点占总数据长度的比例。

    返回:
    - numpy数组: 转换后的时间序列数据。
    - numpy数组: 转换后的标签。
    """
    np.random.seed(int(seed))
    n = int(len(data) * outlierRatio)
    index = np.random.choice(len(data), n, replace=False)

    data_new = data.copy()
    data_new[index] = data_new[index] + 5 * np.std(data)  # 在离群点处增加5倍标准差的幅度

    label_new = label.copy()

    label_new[index] = 1  # 将离群点标记为1

    return data_new, label_new


def flat_region(data, label, contamination, period, seed=5):
    """
    将时间序列数据的特定区域替换为平坦区域。

    参数:
    - data (numpy数组): 时间序列数据。
    - label (numpy数组): 二进制标签，指示异常点（1）和正常点（0）。
    - contamination (浮点数): 污染比例，表示需要转换的时间段占总长度的比例。
    - period (整数): 最小时间段的长度。
    - seed (整数): 随机数生成的种子，用于可重复性。

    返回:
    - numpy数组: 转换后的时间序列数据。
    - numpy数组: 转换后的标签。
    """
    region = select_region(len(data), contamination, period, seed)

    data_new = data.copy()
    label_new = label.copy()
    for r in region:
        data_new[r[0]:r[1]] = data[r[0]]  # 将指定区域替换为该区域的第一个数据点
        label_new[r[0]:r[1]] = 1  # 将该区域标记为1

    return data_new, label_new

def flip_segment(data, label, contamination, period, seed=5):
    """
    翻转原始时间序列的特定段。

    参数:
    - data (numpy数组): 时间序列数据。
    - label (numpy数组): 二进制标签，指示异常点（1）和正常点（0）。
    - contamination (浮点数): 污染比例，表示需要转换的时间段占总长度的比例。
    - period (整数): 最小时间段的长度。
    - seed (整数): 随机数生成的种子，用于可重复性。

    返回:
    - numpy数组: 转换后的时间序列数据。
    - numpy数组: 转换后的标签。
    """
    region = select_region(len(data), contamination, period, seed)

    data_new = data.copy()
    label_new = label.copy()
    for r in region:
        data_new[r[0]:r[1]] = np.flipud(data[r[0]:r[1]])  # 对指定区域进行翻转
        label_new[r[0]:r[1]] = 1  # 将该区域标记为1

    return data_new, label_new


def change_segment_add_scale(data, label, contamination, period, seed=5, para=2, method='scale'):
    """
    更改特定时间段的值并进行缩放。

    参数:
    - data (numpy数组): 时间序列数据。
    - label (numpy数组): 二进制标签，指示异常点（1）和正常点（0）。
    - contamination (浮点数): 污染比例，表示需要转换的时间段占总长度的比例。
    - period (整数): 最小时间段的长度。
    - seed (整数): 随机数生成的种子，用于可重复性。
    - para (整数/浮点数): 缩放因子或增加的值。
    - method (字符串): 变换方法，可以是'scale'（缩放）或'add'（增加）。

    返回:
    - numpy数组: 转换后的时间序列数据。
    - numpy数组: 转换后的标签。
    """
    region = select_region(len(data), contamination, period, seed)

    data_new = data.copy()
    label_new = label.copy()
    if method == 'scale':
        for r in region:
            data_new[r[0]:r[1]] *= para  # 对指定区域进行缩放
            label_new[r[0]:r[1]] = 1  # 将该区域标记为1
    elif method == 'add':
        for r in region:
            data_new[r[0]:r[1]] += para  # 对指定区域进行增加
            label_new[r[0]:r[1]] = 1  # 将该区域标记为1

    return data_new, label_new

def change_segment_normalization(data, label, contamination, period, seed=5, method='Z-score'):
    """
    对特定时间段的数据进行归一化。

    参数:
    - data (numpy数组): 时间序列数据。
    - label (numpy数组): 二进制标签，指示异常点（1）和正常点（0）。
    - contamination (浮点数): 污染比例，表示需要转换的时间段占总长度的比例。
    - period (整数): 最小时间段的长度。
    - seed (整数): 随机数生成的种子，用于可重复性。
    - method (字符串): 归一化方法，可以是'Z-score'、'Min-max'、'MeanNorm'、'MedianNorm'、'UnitLength'、'Logistic'或'Tanh'。

    返回:
    - numpy数组: 转换后的时间序列数据。
    - numpy数组: 转换后的标签。
    """
    region = select_region(len(data), contamination, period, seed)

    data_new = data.copy()
    label_new = label.copy()
    
    for r in region:
        x = data[r[0]:r[1]].copy()

        if method == 'Z-score':
            x = (x - np.mean(x)) / np.std(x)  # Z-score归一化
        elif method == 'Min-max':
            x = (x - np.min(x)) / (np.max(x) - np.min(x))  # Min-max归一化
        elif method == 'MeanNorm':
            x = (x - np.mean(x)) / (np.max(x) - np.min(x))  # Mean normalization归一化
        elif method == 'MedianNorm':
            x /= np.median(x)  # Median normalization归一化
        elif method == 'UnitLength':
            x /= np.sum(x**2)**0.5  # 单位长度归一化
        elif method == 'Logistic':
            x = 1 / (1 + np.exp(-x))  # Logistic归一化
        elif method == 'Tanh':
            y = np.exp(2 * x)
            x = (y - 1) / (y + 1)  # Tanh归一化
        
        data_new[r[0]:r[1]] = x
        label_new[r[0]:r[1]] = 1  # 将该区域标记为1

    return data_new, label_new


def change_segment_partial(data, label, contamination, period, seed=5, ratio=0.2, method='flat'):
    """
    更改特定时间段的数据部分并添加噪声。

    参数:
    - data (numpy数组): 时间序列数据。
    - label (numpy数组): 二进制标签，指示异常点（1）和正常点（0）。
    - contamination (浮点数): 污染比例，表示需要转换的时间段占总长度的比例。
    - period (整数): 最小时间段的长度。
    - seed (整数): 随机数生成的种子，用于可重复性。
    - ratio (浮点数): 更改时间段的部分比例。
    - method (字符串): 变换方法，可以是'flat'（替换为常数值）或'noise'（添加噪声）。

    返回:
    - numpy数组: 转换后的时间序列数据。
    - numpy数组: 转换后的标签。
    """
    region = select_region(len(data), contamination, period, seed)

    data_new = data.copy()
    label_new = label.copy()
    
    for r in region:
        x = data[r[0]:r[1]].copy()
    
        l0 = int(len(x) * ratio)
        if method == 'flat':
            x[:l0] = x[0]  # 将指定时间段的一部分数据替换为该时间段的第一个数据点
        elif method == 'noise':
            x[:l0] += np.random.normal(size=l0) * np.std(x) * 0.3  # 在指定时间段的一部分数据中添加噪声
            
        data_new[r[0]:r[1]] = x
        label_new[r[0]:(r[0] + l0)] = 1  # 将该区域标记为1

    return data_new, label_new

def change_segment_resampling(data, label, contamination, period, seed, resampling_ratio):
    """
    对特定时间段的数据进行重采样。

    参数:
    - data (numpy数组): 时间序列数据。
    - label (numpy数组): 二进制标签，指示异常点（1）和正常点（0）。
    - contamination (浮点数): 污染比例，表示需要转换的时间段占总长度的比例。
    - period (整数): 最小时间段的长度。
    - seed (整数): 随机数生成的种子，用于可重复性。
    - resampling_ratio (浮点数): 重采样的比例，用于调整时间段的长度。

    返回:
    - numpy数组: 转换后的时间序列数据。
    - numpy数组: 转换后的标签。
    """
    region = select_region(len(data), contamination, period, seed)
    
    pre = 0
    tmp_data = []
    tmp_label = []
    for r in region:
        tmp_data += list(data[pre:r[0]])
        tmp_label += list(label[pre:r[0]])
        x = data[r[0]:r[1]].copy()
    
        length_new = int((r[1] - r[0]) * resampling_ratio)
        f = signal.resample(x, length_new)  # 使用SciPy库的resample函数进行重采样
        
        tmp_data += list(f)
        tmp_label += [1] * len(f)
        
        pre = r[1]
        
    tmp_data += list(data[pre:len(data)])
    tmp_label += list(label[pre:len(data)])
 
    return np.array(tmp_data), np.array(tmp_label)

# 后面的内容就是引用上面的方法了

24.5.2 重点源码 TSB_UAD / transformer / sbd_distance.py

import numpy as np
from numpy.linalg import norm
from numpy.fft import fft, ifft

def roll_zeropad(a, shift, axis=None):
    """
    将数组a沿指定轴进行循环滚动（roll），并在滚动过程中用零进行填充。

    参数:
    - a (numpy数组): 待滚动的数组。
    - shift (整数): 滚动的步数，正数表示向左滚动，负数表示向右滚动。
    - axis (整数): 沿指定轴进行滚动。默认为None，表示对整个数组进行滚动。

    返回:
    - numpy数组: 滚动后的数组。
    """
    a = np.asanyarray(a)
    if shift == 0:
        return a
    if axis is None:
        n = a.size
        reshape = True
    else:
        n = a.shape[axis]
        reshape = False
    if np.abs(shift) > n:
        res = np.zeros_like(a)
    elif shift < 0:
        shift += n
        zeros = np.zeros_like(a.take(np.arange(n-shift), axis))
        res = np.concatenate((a.take(np.arange(n-shift, n), axis), zeros), axis)
    else:
        zeros = np.zeros_like(a.take(np.arange(n-shift, n), axis))
        res = np.concatenate((zeros, a.take(np.arange(n-shift), axis)), axis)
    if reshape:
        return res.reshape(a.shape)
    else:
        return res
    
def _ncc_c(x, y):
    """
    计算归一化互相关系数（Normalized Cross-Correlation，NCC）。

    参数:
    - x (numpy数组): 第一个数组。
    - y (numpy数组): 第二个数组。

    返回:
    - numpy数组: 归一化互相关系数。
    """
    den = np.array(norm(x) * norm(y))
    den[den == 0] = np.Inf

    x_len = len(x)
    fft_size = 1 << (2 * x_len - 1).bit_length()
    cc = ifft(fft(x, fft_size) * np.conj(fft(y, fft_size)))
    cc = np.concatenate((cc[-(x_len-1):], cc[:x_len]))
    return np.real(cc) / den

def _sbd(x, y):
    """
    计算标准化互相关分布（Standardized Cross-Correlation Distribution，SBD）。

    参数:
    - x (numpy数组): 第一个数组。
    - y (numpy数组): 第二个数组。

    返回:
    - 元组: 包含SBD距离和经过滚动的第二个数组。
    """
    ncc = _ncc_c(x, y)
    idx = ncc.argmax()
    dist = 1 - ncc[idx]
    yshift = roll_zeropad(y, (idx + 1) - max(len(x), len(y)))

    return dist, yshift

24.5.3 重点源码 TSB_UAD / transformer / artificialConstruction.py

import numpy as np
import networkx as nx 
import math
from .sbd_distance import _sbd

# 计算SBD距离矩阵
def construct_sbd_matrix(X_train, y_train):
    n_indexed = len(y_train)
    X_train_distance = np.zeros([n_indexed,n_indexed])
    
    for i in range(n_indexed):
        for j in range(i+1,n_indexed):
            X_train_distance[i][j] = max(_sbd(X_train[i], X_train[j])[0], 0)
            X_train_distance[j][i] = X_train_distance[i][j]
    
    np.fill_diagonal(X_train_distance, 1e4)

    closest = np.argmin(X_train_distance, axis=0)
    y_pred = y_train[closest]

    n_label = len(np.unique(y_train))

    confusionMatrix = np.zeros((n_label, n_label))
    
    for i in range(n_label):    # 真实标签为 i+1
        for j in range(n_label):  # 预测标签为 j+1
            tmp1 = y_train == (i+1)
            tmp2 = y_pred == (j+1)
            confusionMatrix[i][j] = np.sum(tmp1 * tmp2) / np.sum(tmp1)
            
    adjacencyMatrix = (confusionMatrix + confusionMatrix.T) / 2 + 1e-3
    # np.fill_diagonal(adjacencyMatrix, 0)
    return adjacencyMatrix

# 基于最大生成树的聚类
def clustering_mst(adjacencyMatrix):
    G = nx.from_numpy_matrix(adjacencyMatrix, parallel_edges=False)
    T = nx.maximum_spanning_tree(G, weight='weight')
        
    n_label = len(adjacencyMatrix)
    labelList = [-1] * n_label
    labelList[0] = 0
    
    # BFS
    visited = [0]
    queue = [0]
    while queue:
        s = queue.pop(0)
        for neighbor in T.neighbors(s):
            if neighbor not in visited:
                visited.append(neighbor)
                queue.append(neighbor)
                labelList[neighbor] = 1 - labelList[s]
                       
    if len(np.unique(labelList)) != 2:
        print('Class Separation Error')
        return
        
    labelList = np.array(labelList)
    return labelList

# 基于两个聚类构造异常样本
def construct_anomaly(X_train, y_train, clusterIndex, K=3, anomalyRatio=0.05, seed=0, return_statistics=False):
    np.random.seed(seed)
    
    # K 是异常数量，获得正常数量
    N_normal_seg = int(K / anomalyRatio)
    
    ano_labels = np.where(clusterIndex == 1)[0] + 1  # 异常标签列表，加1因为标签索引从1开始
    nor_labels = np.where(clusterIndex == 0)[0] + 1  # 正常标签列表
    
    # 异常标签在 y_train 中的索引
    ano_index = [i for i in range(len(y_train)) if y_train[i] in ano_labels]
    K = min(K, len(ano_index))
    # 在 y_train 中选择 K 个异常样本
    ano_index_selected = np.random.choice(ano_index, size=K, replace=False)
    
    # 对应的 K 个真实标签 
    ano_label_selected = y_train[ano_index_selected]
    
    # 最频繁选择的标签
    ano_label_mostfreq = max(ano_label_selected.tolist(), key=ano_label_selected.tolist().count)
    freq_ano_label_mostfreq = sum(ano_label_selected == ano_label_mostfreq)
    
    # 每个正常标签的最小频数
    freq_nor_label_min = 20 * freq_ano_label_mostfreq  
    # 将要使用的正常标签的数量
    num_nor_label = min(math.ceil(N_normal_seg / freq_nor_label_min), len(nor_labels))  
    # 每个正常标签的实际频数，这里每个正常标签的基数相同
    freq_nor_label = math.ceil(N_normal_seg / num_nor_label) 
    
    # 选择的正常标签
    nor_labels_selected = np.random.choice(nor_labels, size=num_nor_label, replace=False)
    # 在 y_train 中的选择的索引
    nor_index_selected = []
    for item in nor_labels_selected:
        tmp = np.where(y_train == item)[0]
        nor_index_selected_item = np.random.choice(tmp, size=freq_nor_label, replace=True)
        nor_index_selected.append(nor_index_selected_item)

  。。......
    
        # NC
        nor_dist_array = sbd_matrix[:len(X_nor), :len(X_nor)].ravel()
        nor_dist_array = nor_dist_array[nor_dist_array < 2]
        avg_nor = np.mean(nor_dist_array)
        
        ano_dist_array = sbd_matrix[len(X_nor):n, len(X_nor):n].ravel()
        ano_dist_array = ano_dist_array[ano_dist_array < 2]
        avg_ano = np.mean(ano_dist_array)
        
        nc = np.sqrt(avg_nor / avg_ano)
        
        # NA
        if num_nor_label == 1:
            na = 1
        else:
            # 根据标签拆分索引
            cluster_index_basedon_label_