611. 有效三角形的个数

原题链接

---

首先看题干，非负整数数组，三元组数
所以，我们可知，这个数组最少有三个元素，这样才能组成三元组

在解题之前，我们补充一点：
给我们三个数，怎么判断是不是能不能构成三角形呢？
我们一般的判断都是任意两边之和大于第三边，但是如果在时间复杂度的位置上考虑，比三次太麻烦
这个时候，我们想，如果让这个数组是有序的，对比的这三个边是有序的，那么两个较短的边相加，大于第三边，是不是就可以说明前面两条边任意一条和后面的相加，都大于其余一条边呢？

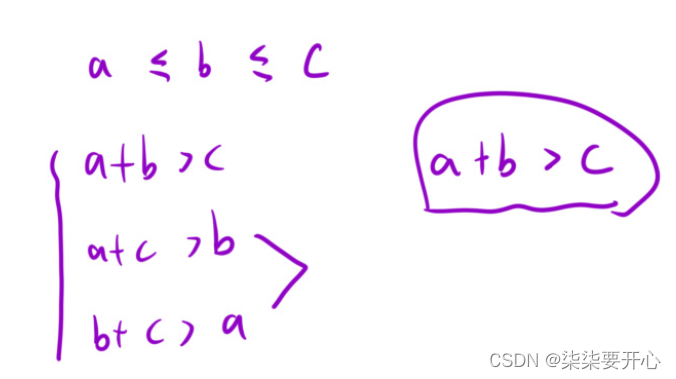
很明显，这样是可以的，所以我们的算法就进一步进行了优化

---

题解：

1、暴力枚举 O(N)
暴力算法就是写三个 for 循环嵌套，在最里面的一层 for 循环判断三个数是否能组成三角形

这个算法虽然可以算出，但是由于时间复杂度太高，会导致超时

2、利用单调性，使用双指针算法解决问题
（0）排序
（1）先固定最大的数
（2）在最大的数的左区间，使用双指正，快速统计出符合要求的三元组个数

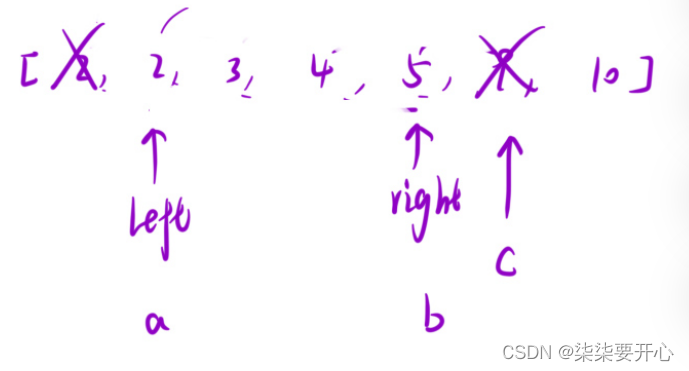
我们先看这个数组，我们先把最后一个数字固定，定义 left 和 right，
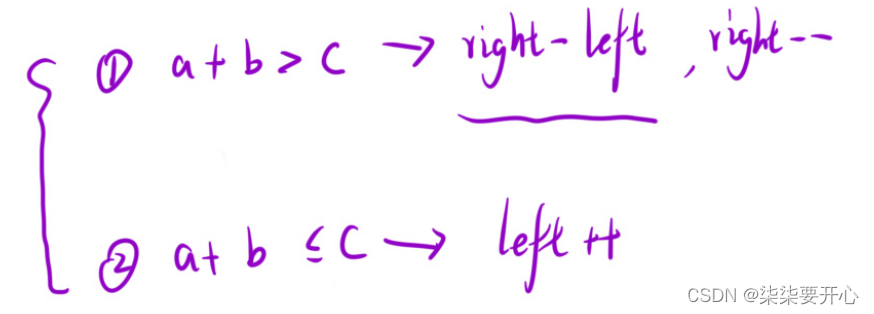
让left + right，如果大于 最后一个数字，那么left 右边的所有数字和 right 相加都大于，所以中间的统计下来，right –
如果小于，那么left++，再次判断

---

代码：

class Solution {
    public int triangleNumber(int[] nums) {
        //1.优化：排序
        Arrays.sort(nums);

        //2.利用双指针解决问题
        int ret = 0;
        int n = nums.length;
        for (int i = n - 1; i >= 2; i--) {//先固定最大的数
            //利用双指针快速统计处符合要求的三元组的个数
            int left = 0;
            int right = i-1;
            while (left < right) {
                if (nums[left] + nums[right] > nums[i]) {
                    ret += right - left;
                    right--;
                }else {
                    left++;
                }
            }
        }
        return ret;
    }
}

LCR 179. 查找总价格为目标值的两个商品

原题链接

---

先看题干，升序数组，两个数相加等于 target
很好，这道题非常简单

题解：

1、暴力枚举 O(N2)
运用暴力枚举可以直接用两个 for 循环嵌套，然后再循环内部相加判断是不是和 target 相等

这个方法虽然很简单，但是时间复杂度过高，会超出时间

2、利用单调性，使用双指针解决问题
这个时候，我们依然使用我们非常熟悉的单调性和双指针

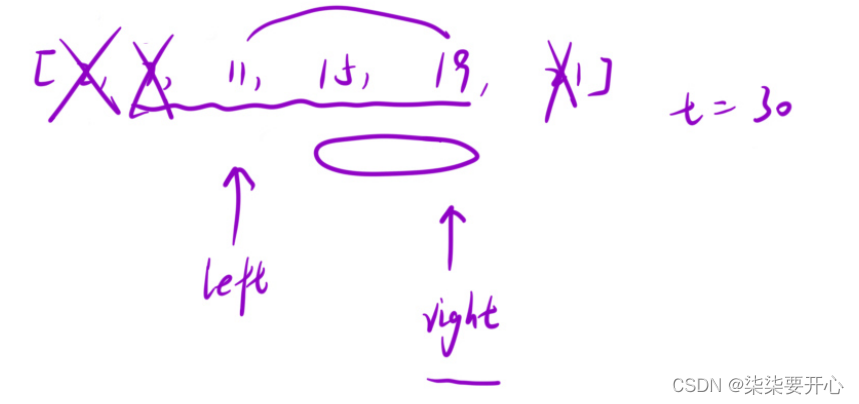
先判断left 和 right 相加
如果 大于 t ，right–
如果 小于 t ，left++
如果相等，直接返回

---

代码：

public int[] twoSum(int[] price, int target) {
        int left = 0;
        int right = price.length-1;
        while (left < right) {
            int sum = price[left] + price[right];
            if (sum > target) {
                right--;
            }else if (sum < target) {
                left++;
            }else {
                return new int[]{price[left],price[right]};
            }
        }
        return new int[]{0};
    }