例一
动态聚类,K-means法,随机选取凝聚点(题目直接给出)
已知5个样品的观测值为:1,4,5,7,11。试用K均值法分为两类(凝聚点分别取1,4与1,11)
解:以1,4为例
STEP1确定凝聚点:X1和X5
STEP2确定初始分类,
G
1
(
0
)
{G_1^{(0)}}
G1(0)={x1,x2,x3},
G
2
(
0
)
{G_2^{(0)}}
G2(0)={x4,x5}
STEP3重新计算各类的重心,以其作为新的凝聚点,分别为3.3和9
STEP4 以新的重心为凝聚点重新修改分类,结果不变,故聚类结果为
G
1
{G_1}
G1={x1,x2,x3},
G
2
{G_2}
G2={x4,x5}
例二
动态聚类,K-means法,还是上面的例子,使用密度法选取凝聚点
已知5个样品的观测值为:1,4,5,7,11。试用K均值法分为三类。
密度法:
- 首先计算出每个样品的密度,密度即:以正数d为半价,样品为球心,落在球内的样品数;
- 选择密度最大的样品作为第一凝聚点;
- 人为确定一个正数D(一般D>d),若次大密度样品点与第一凝聚点距离大于D则作为第二个凝聚点,否则舍去,选取密度次于它的样品;
解:d=2,D=3.5
STEP1计算出每个样品的密度
| x1 | x2 | x3 | x4 | x5 | |
|---|---|---|---|---|---|
| 密度 | 0 | 1 | 2 | 1 | 0 |
因此第一凝聚点为x3,次大密度样品点位x2和x4,但它们与x3的距离小于D,故舍去,选取x1和x5作为第二凝聚点;
STEP2确定初始分类,除凝聚点之外的样品点按照最小距离原则确定它们的分类
G
1
(
0
)
{G_1^{(0)}}
G1(0)={x1},
G
2
(
0
)
{G_2^{(0)}}
G2(0)={x2,x3,x4},
G
3
(
0
)
{G_3^{(0)}}
G3(0)={x5}。
STEP3重新计算各类的重心,以其作为新的凝聚点
三类重心分别为:1,5.3,11
STEP4 重新确定各样品归属的类别:
G
1
(
1
)
{G_1^{(1)}}
G1(1)={x1},
G
2
(
1
)
{G_2^{(1)}}
G2(1)={x2,x3,x4},
G
3
(
1
)
{G_3^{(1)}}
G3(1)={x5}
若与上一次分类的结果不同,需要继续计算各类的重心,重新分类。可以看到这次的分类结果与上一次相同,因此算法终止,聚类结果为 G 1 {G_1} G1={x1}, G 2 {G_2} G2={x2,x3,x4}, G 3 {G_3} G3={x5}。
例三
[应用多元统计分析(高惠璇版)6-3]
系统聚类法——最长距离、类平均法

系统聚类法基本思想 :设有n个样品,每个样品m项指标。首先将n个样品视为n类,计算类间距离(此时类间距离与样品间距离是等价的),选取 距离最近 的两类合并成新类,并计算新类与其他类的距离,再按最小距离原则并类,每次合并一类直至所有样品都并成一类。
最长距离法
最长距离法和最短距离法的本质是一样的,计算类与类的距离时使用下面的公式:
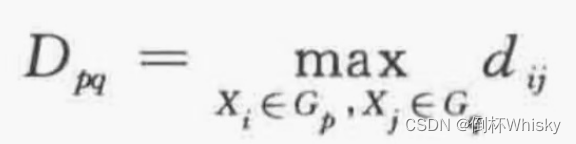
STEP1从初始矩阵出发,选择类间距离最小的合并为一类,即并类距离
D
1
{D_1}
D1=1
合并x1和x4,记CL4={x1,x4},画出距离矩阵
D
(
1
)
{D^{(1)}}
D(1)
其他类
x
i
{x_i}
xi(i=2、3、5)到CL4的距离为:
x
i
{x_i}
xi到x1的距离与
x
i
{x_i}
xi到x4的距离中最大的那个
D
(
1
)
{D^{(1)}}
D(1)=
[
x
2
x
3
x
5
C
L
4
x
2
0
x
3
9
0
x
5
3
5
0
C
L
4
7
10
8
0
]
\begin{bmatrix} & x2 & x3 & x5& CL4 \\ x2 & 0 & \\ x3 & 9 & 0 \\ x5 & 3 & 5 &0 \\ CL4 & 7 & 10 &8 &0 \end{bmatrix}
x2x3x5CL4x20937x30510x508CL40
STEP2同样选择类间距离最小的合并为一类,x2和x5的距离最近,并类距离
D
2
{D_2}
D2=3
合并x2和x5,记CL3={x2,x5},画出距离矩阵
D
(
2
)
{D^{(2)}}
D(2)
x3到CL4和CL3的距离计算和上面一样
D ( 2 ) {D^{(2)}} D(2)= [ x 3 C L 4 C L 3 x 3 0 C L 4 10 0 C L 3 9 8 0 ] \begin{bmatrix} & x3 & CL4 & CL3 \\ x3 & 0 & \\ CL4 & 10 & 0 \\ CL3 & 9 & 8 &0 \\ \end{bmatrix} x3CL4CL3x30109CL408CL30
STEP3选择类间距离最小的合并为一类,CL4和CL3的距离最近,并类距离
D
3
{D_3}
D3=8
合并CL3和CL4,记CL2={x1,x2,x4,x5},画出距离矩阵
D
(
3
)
{D^{(3)}}
D(3)
D ( 3 ) {D^{(3)}} D(3)= [ x 3 C L 2 x 3 0 C L 2 10 0 ] \begin{bmatrix} & x3 & CL2 \\ x3 & 0 & \\ CL2 & 10 & 0 \\ \end{bmatrix} x3CL2x3010CL20
STEP4将所有类合并为一类,CL1={x1,x2,x3,x4,x5},并类距离
D
4
{D_4}
D4=10
D ( 4 ) {D^{(4)}} D(4)= [ C L 1 C L 1 0 ] \begin{bmatrix} & CL1 \\ CL1 & 0 & \\ \end{bmatrix} [CL1CL10]
STEP5画出谱系聚类图

类平均法
类平均法的类间距离计算公式如下
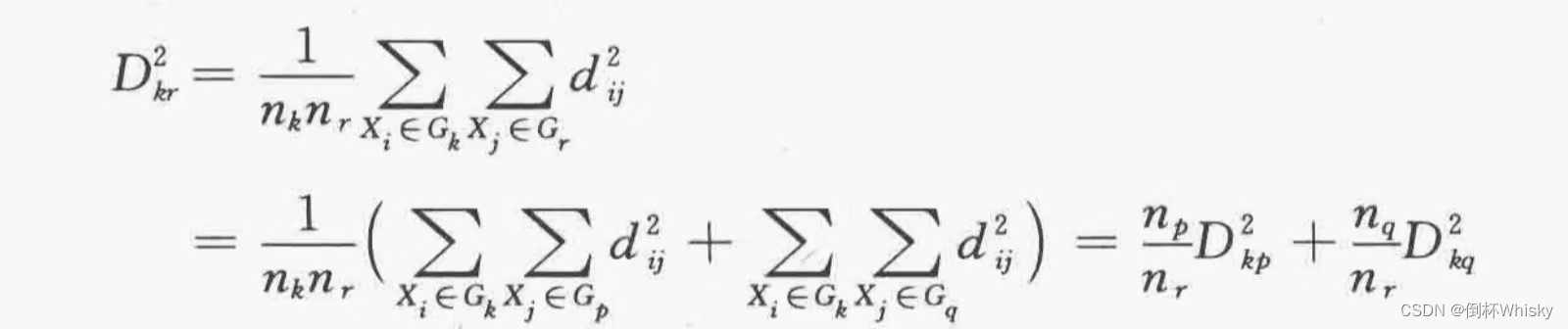
具体步骤和上面类似,不同的是在计算类间距离的不同。这里使用距离的平方。
STEP1从初始矩阵出发,选择类间距离最小的合并为一类,即并类距离
D
1
{D_1}
D1=1
合并x1和x4,记CL4={x1,x4},画出距离矩阵
D
(
1
)
{D^{(1)}}
D(1)
其他类
x
i
{x_i}
xi(i=2、3、5)到CL4的距离为:
以x2到CL4的距离为例,其他的同理:
D
2
{D^2}
D2=
1
2
{1 \over 2}
21
D
21
2
{D_{21}^2}
D212+
1
2
{1 \over 2}
21
D
24
2
{D_{24}^2}
D242=
1
2
{1 \over 2}
21× 4²+
1
2
{1 \over 2}
21× 7²=65/2
所以可以画出的距离矩阵为:
D
(
1
)
{D^{(1)}}
D(1)=
[
x
2
x
3
x
5
C
L
4
x
2
0
x
3
9
2
0
x
5
3
2
5
2
0
C
L
4
65
/
2
136
/
2
100
/
2
0
]
\begin{bmatrix} & x2 & x3 & x5& CL4 \\ x2 & 0 & \\ x3 & 9² & 0 \\ x5 & 3² & 5² &0 \\ CL4 & 65/2 & 136/2 &100/2 &0 \end{bmatrix}
x2x3x5CL4x20923265/2x3052136/2x50100/2CL40
STEP2同样选择类间距离最小的合并为一类,x2和x5的距离最近,并类距离
D
2
{D_2}
D2=3
合并x2和x5,记CL3={x2,x5},画出距离矩阵
D
(
2
)
{D^{(2)}}
D(2)
CL4到CL3的距离计算如下:
D 2 {D^2} D2= 1 2 {1 \over 2} 21 D ( C L 4 ) 2 2 {D_{(CL4)2}^2} D(CL4)22+ 1 2 {1 \over 2} 21 D ( C L 4 ) 5 2 {D_{(CL4)5}^2} D(CL4)52= 1 2 {1 \over 2} 21× (65/2)+ 1 2 {1 \over 2} 21× (100/2)=165/4
D ( 2 ) {D^{(2)}} D(2)= [ x 3 C L 4 C L 3 x 3 0 C L 4 136 / 2 0 C L 3 106 / 2 165 / 4 0 ] \begin{bmatrix} & x3 & CL4 & CL3 \\ x3 & 0 & \\ CL4 & 136/2 & 0 \\ CL3 & 106/2 & 165/4 &0 \\ \end{bmatrix} x3CL4CL3x30136/2106/2CL40165/4CL30
STEP3选择类间距离最小的合并为一类,CL4和CL3的距离最近,并类距离
D
3
{D_3}
D3=
165
/
4
\sqrt{165/4}
165/4
合并CL3和CL4,记CL2={x1,x2,x4,x5},画出距离矩阵
D
(
3
)
{D^{(3)}}
D(3)
D ( 3 ) {D^{(3)}} D(3)= [ x 3 C L 2 x 3 0 C L 2 121 / 2 0 ] \begin{bmatrix} & x3 & CL2 \\ x3 & 0 & \\ CL2 & 121/2 & 0 \\ \end{bmatrix} x3CL2x30121/2CL20
STEP4将所有类合并为一类,CL1={x1,x2,x3,x4,x5},并类距离
D
4
{D_4}
D4=
121
/
2
\sqrt{121/2}
121/2
D ( 4 ) {D^{(4)}} D(4)= [ C L 1 C L 1 0 ] \begin{bmatrix} & CL1 \\ CL1 & 0 & \\ \end{bmatrix} [CL1CL10]
STEP5画出谱系聚类图
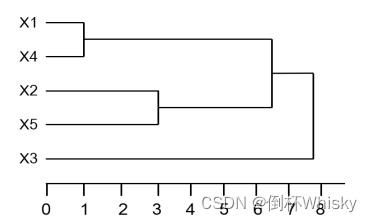
(注:无论用什么系统聚类法,在并类时都是选择类间距离最小的两个类,使用最长距离法/类平均法/···的区别只是在计算类与类之间的距离时不同)