还是那句话,专心做好你自己的,老老实实把基础打好,不要被其他人带跑节奏,不要跟他打,跟着这系列博客,稳扎稳打一步一步来。即使你VMware workstation没下载好,即使你Ubuntu虚拟机没配好,即使你不知道怎么使用VS code,即使你不知道怎么检查运算符,即使你不知道怎么核对答案,都没有关系。哪怕他们会用Github,哪怕他们有chatgpt账号,哪怕他们在炫耀什么gnome,都不要害怕。
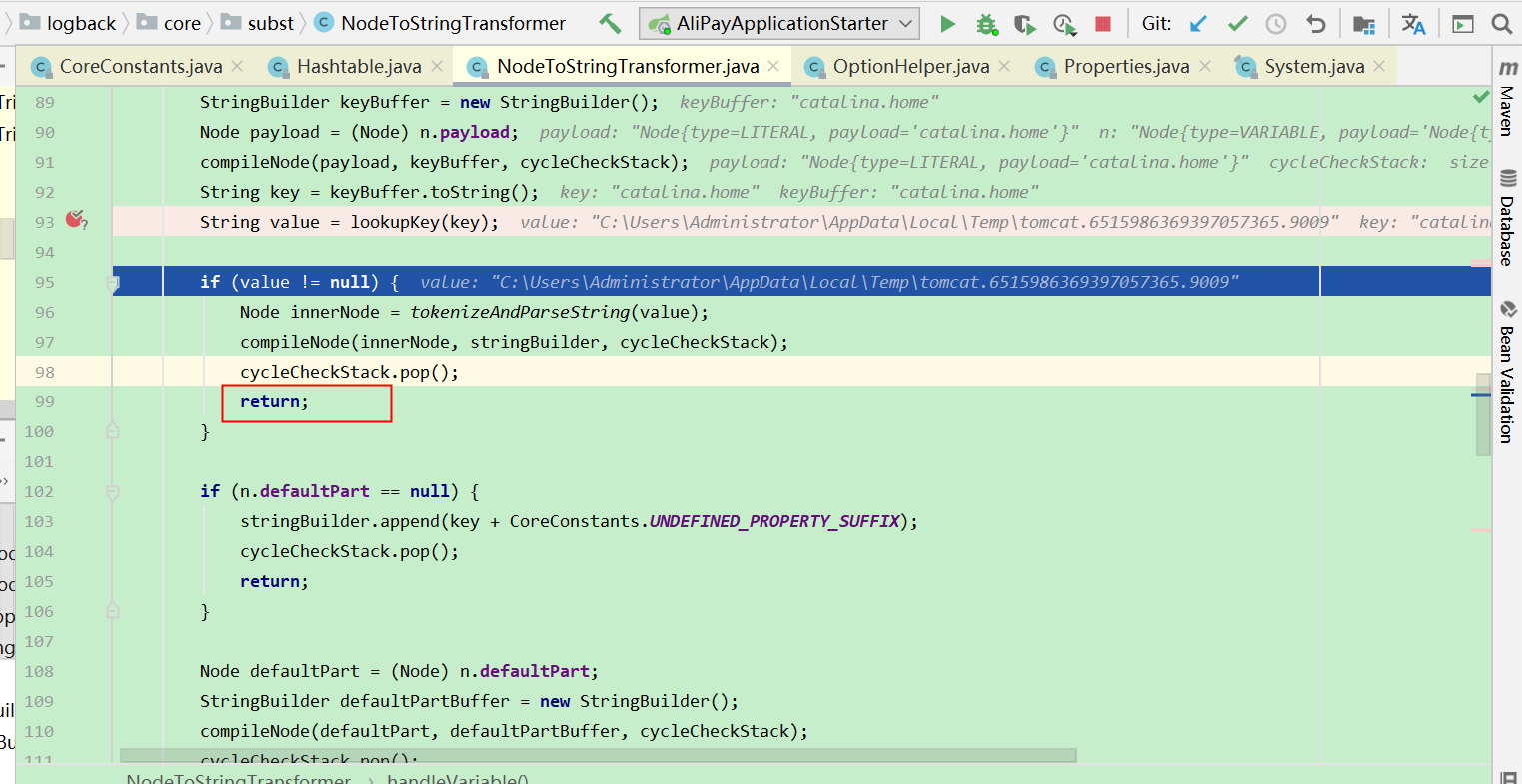
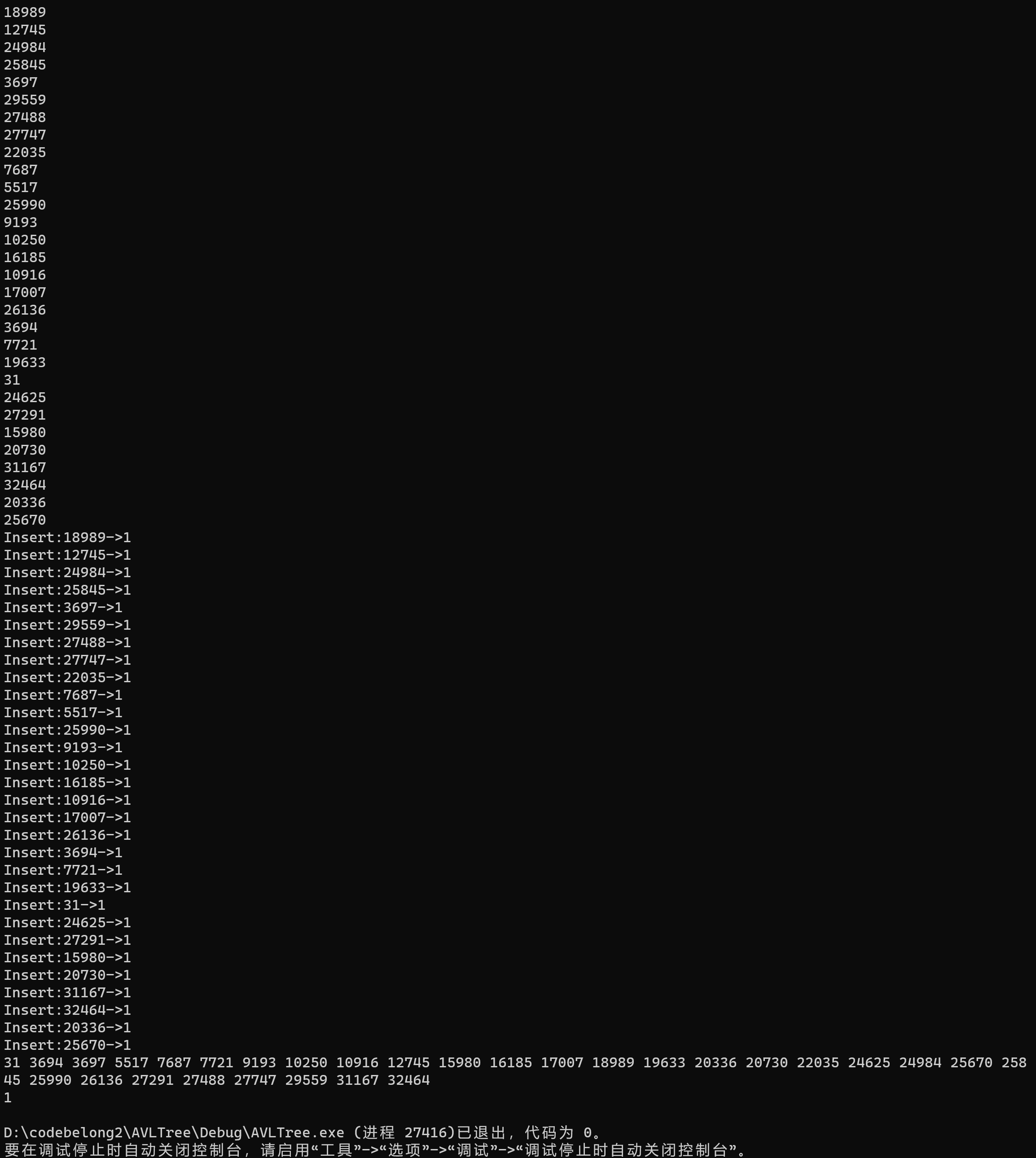
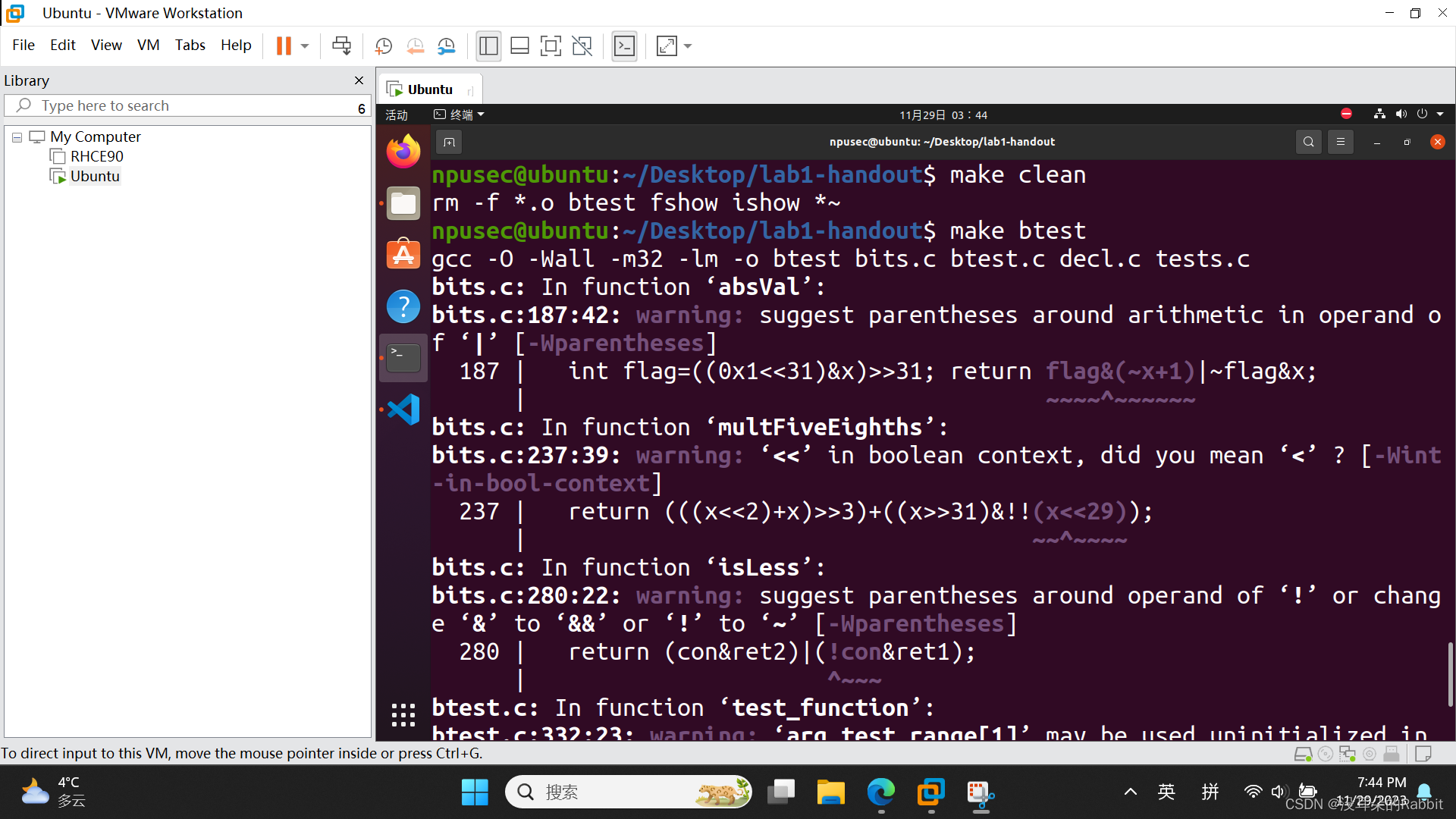
接着是第9个函数,int isLess(int x, int y),如果x<y,那么就返回1,反之返回0。比如说,因为4小于5,所以isLess(4,5) = 1。那么如何判断x<y呢?我们可以分为一下两种情况:x与y同号,x与y异号。第一种情况,当x与y异号,即当!((x>>31)^(y>>31))的值为0时,只需返回~(x>>31)+1即可,为什么呢?因为如果x为正数,则y为负数,此时x<y是不成立的,应该返回0,而此时x>>31=0x0,~(x>>31)为0xFFFFFFFF,~(x>>31)+1为0x0,正好是应该返回的0,如果x为负数,则y为正数,此时x<y成立,应该返回1,而此时x>>31=0xFFFFFFFF,~(x>>31)为0x0,~(x>>31)+1为0x1,正好是应该返回的1。所以针对第一种情况,我们写出表达式"return ~(x>>31)+1"。而第二种情况,x与y同号,即当!((x>>31)^(y>>31))的值为1时,此时可以使用x-y,如果x<y的话,x-y<0,即x-y的最高位也就是符号位为1(因为只允许使用int型变量,而int型变量采取的形式是二进制补码形式,最高位即为符号位)。那么如何计算x-y呢?毕竟不允许使用-运算符,而根据加法与减法的关系,可以知道x-y=x+~y+1。所以如果((x+~y+1)>>31)&0x1为1,就说明(x+~y+1)>>31为0xFFFFFFFF,进而说明(x+~y+1)的最高位为1(因为右移是算术右移),进而说明x-y是负数,进而说明x<y。所以针对于第二种情况,我们写出表达式"return ((x+~y+1)>>31)&0x1;"。综合上述两种情况,我们该返回什么呢?先设置第一种情况的返回值的表达式为"int ret1=~(x>>31)+1;",接着设置第二种情况的返回值的表达式为"int ret2=((x+~y+1)>>31)&0x1;",而判断该返回ret1还是ret2的表达式为"con=!((x>>31)^(y>>31))"。这下子可以写出"return (con&ret2)|(!con&ret1);"当con为1时,完全可以忽略(!con&ret1),而只选择看(con&ret2),这时返回的是ret2,符合我们的推理。当con为0时,忽略(con&ret2),而只选择看(!con&ret1),此时返回的是ret1,也符合我们的推理。接着仿照与前8个函数同样的步骤,我们写出了第9个函数并验证了它是否满足运算符的要求,以及是否正确,如(图1:第9个函数)所示。
**************************************************************************************************************


 (图1:第9个函数)
(图1:第9个函数)
**************************************************************************************************************
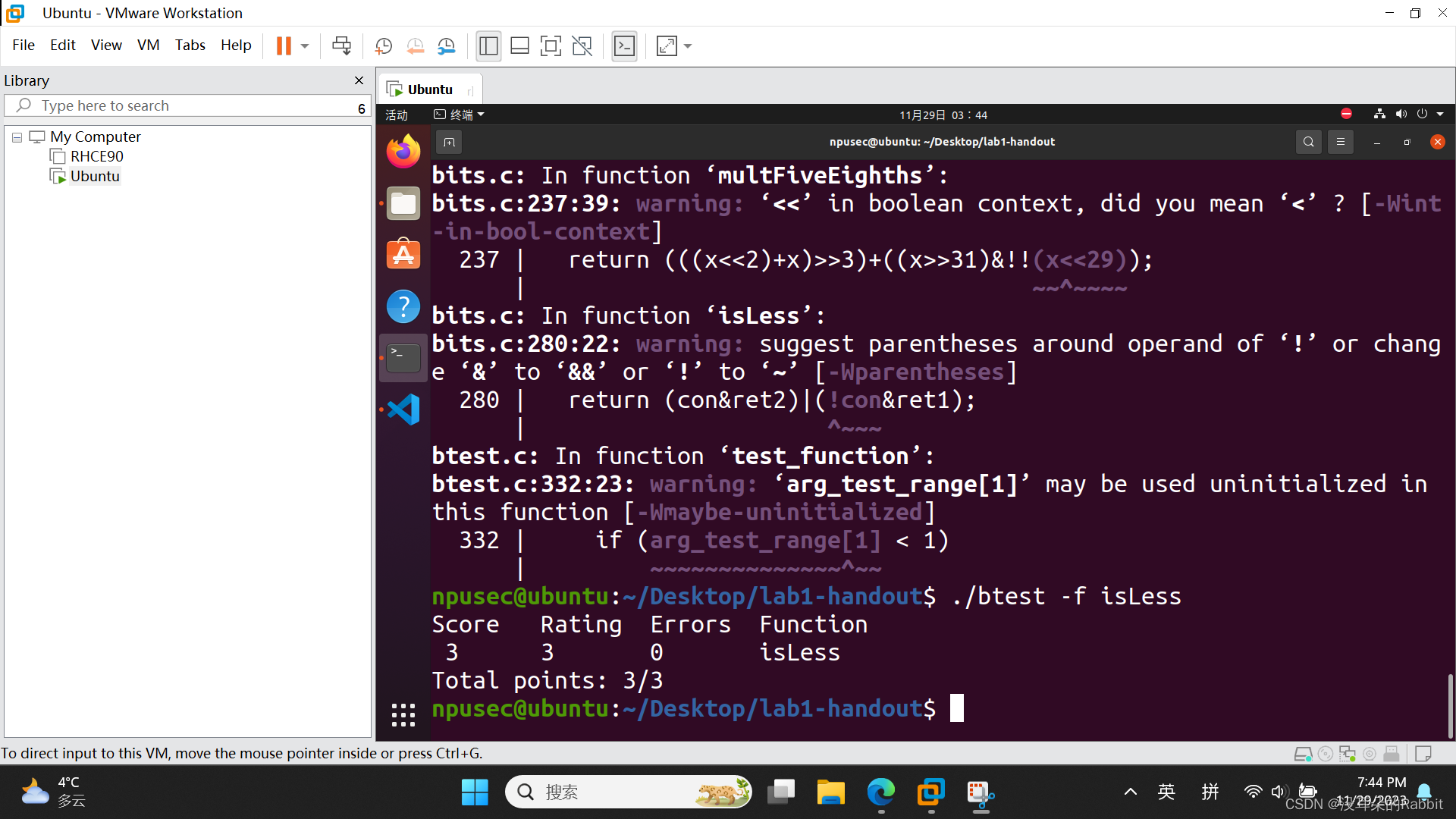
接着,看第10个函数,int isLessOrEqual(int x, int y),第10题在第9题的基础上,额外要求,如果x=y,也需要返回1。那么我们在我们做出的第9题的答案的基础上,具体分析看一看是否满足第10题提出的额外的这个条件。首先因为x=y,所以x与y一定是同号,属于第9题中的第二种情况,而第9题中的第2种情况计算了x-y,即计算了x+~y+1。当x=y=0x9FFF FFFF(随便举个例子,为了方便理解)时,~y=0x6000 0000,~y+1=0x6000 0001,x+~y+1=0x0,当 x=y=0x7FFF FFFF时,~y=0x8000 0000,~y+1=0x8000 0001,x+~y+1=0x0,第9题中的ret2的表达式为"((x+~y+1)>>31)&0x1",而此时无论相等的x和y同正还是同负,((x+~y+1)>>31)&0x1都为0,注意!!!我们期望的是,如果x=y,也需要返回1,而不是返回0!!!所以我们还需要再进行额外的判断。当然,当x=y时,x^y=0,其它情况下,x^y均不为0。所以利用这一性质,我们只需要小小的修改return语句的表达式即可,修改为"return (con&(ret2|!(x^y)))|(!con&ret1)",这个修改说明,当con为1,也就是x与y同号时,如果ret2为0,则需要再稍微停留一会儿,再思考一下!(x^y),也就是x与y是否相等。当然,有些同学感觉似乎有点感觉了,但感觉又不是很明显,不用担心,等到了大一下学期学习离散数学时,深入学习集合的知识,你们会明白更多的。仿照第9个函数的剩余步骤,如(图2:第10个函数)所示。
**************************************************************************************************************



(图2:第10个函数)
**************************************************************************************************************
休息一会儿之后,我们来看第11个函数, int trueFiveEighths(int x),其在第6个函数的基础上,额外要求避免溢出。这里的避免溢出是什么意思呢?意思是在第6个函数中,我们给出的表达式还原了C语言表达式x*5/8,虽然5/8是一个小数,只要x是在int的表示范围内,那么x*5/8的最终结果也一定在int的表示范围内。只不过C语言表达式会先计算x*5,在计算/8,“先计算x*5”就引入了溢出的可能,所以我们需要想办法改正这一点。怎么改正呢?把我们编写的第6个函数返回的表达式拿过来,"return (((x<<2)+x)>>3)+((x>>31)&!!(x<<29));",针对其中的(((x<<2)+x)>>3),我们可以将其化简成(x>>1)+(x>>3),这样子都是算术右移,就不会造成溢出了。当然,这只是大体的框架,具体还需要怎样的细调,还需要我们去结合题意修改。通过与自己写的C程序做比对,如(图3:与自己写的C程序做比对)所示,我们发现,对于正数x,当x的最低位字节为5, 7, d, f时,返回值还需要在(x>>1)+(x>>3)的基础上加1,而如何表示正数x且x的最低位字节为5, 7, d, f呢?!(x>>31)&!((x&0x5)^0x5)。而对于负数x,我们发现更加复杂,当x的最低位字节为5, 7, d, f时,返回值还需要额外再加2,如果最低位字节为0或者8,则不需要添加,如果最低位字节为除了57df与08之外的其它,则只需要加1。我们的思路如(图3:第11个函数的思路)所示。当然如果你看不懂这个思路也没有关系,大胆往后做,我会慢慢讲。接着仿照前10个函数的思路,如(图4:第11个函数)所示:
**************************************************************************************************************

(图3:第11个函数的思路)
**************************************************************************************************************
**************************************************************************************************************



(图4:第11个函数)
**************************************************************************************************************
第12个函数,int parityCheck(int x), 如果x包含奇数个1,那么返回1,反之返回0。拿int型变量a=0x7FFF FFFF举例来说,我们想让其最终返回的结果为1。现在来看,让a的前一半字节与后一半字节做异或操作,即0x7FFF^0xFFFF,得到了0x1000,接着让0x1000的前一半字节与后一半字节做异或操作,即0x10^0x00,得到了0x10,接着0x1^0x0得到了0x1,接着00B与01B做异或操作,得到了01B,接着0B与1B做异或操作,得到了1B,正好是我们想让其最终返回的结果。按照这个思路,我们可以写出相应的代码,并且仿照前11个函数相同的操作,验证我们写出的表达式的正确性,如(图5:第12个函数)所示。另外,第12个函数的代码很简洁,甚至有些匪夷所思,但是这是正常的,慢慢来嘛。
**************************************************************************************************************



(图5:第12个函数)
**************************************************************************************************************
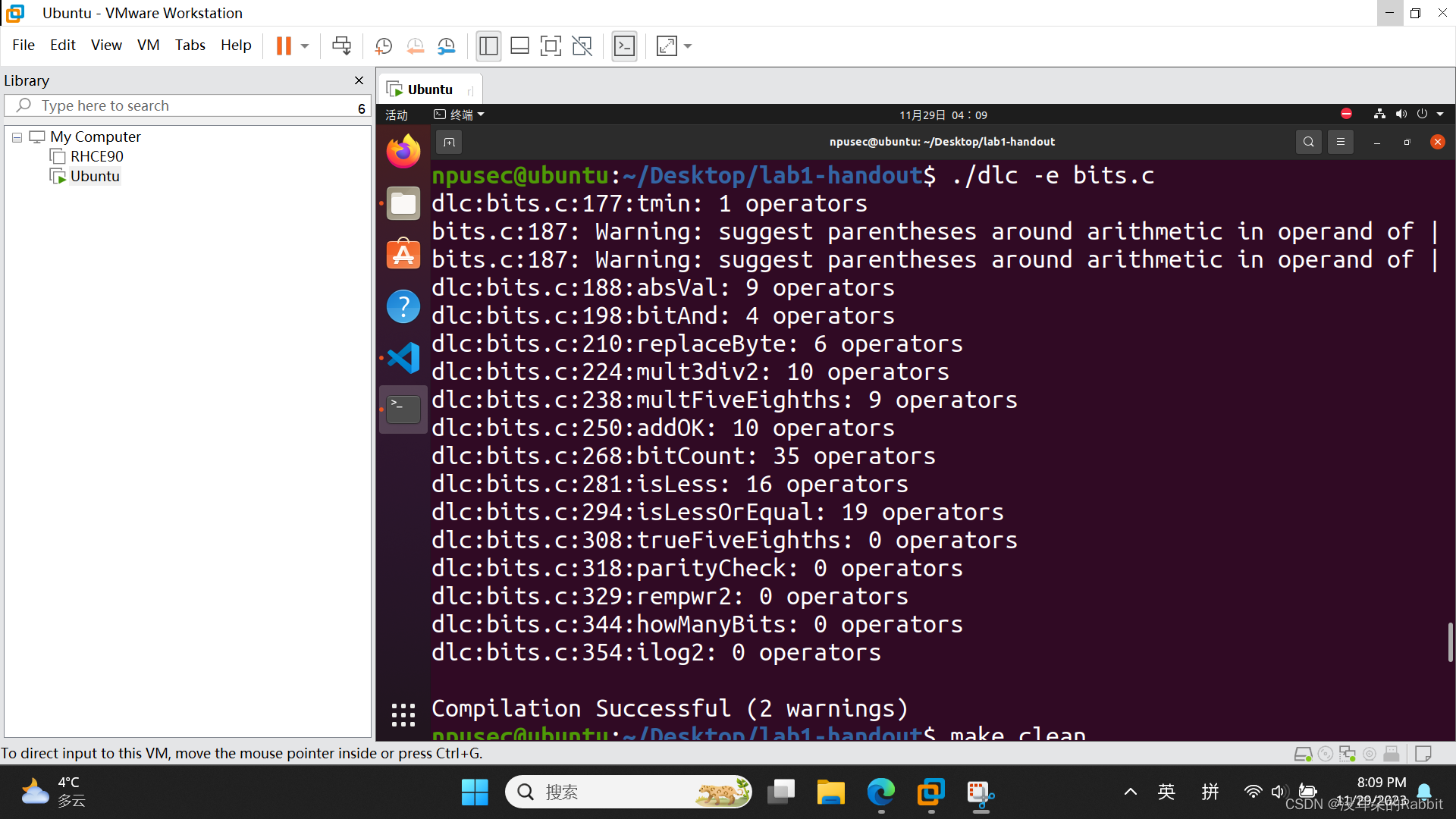
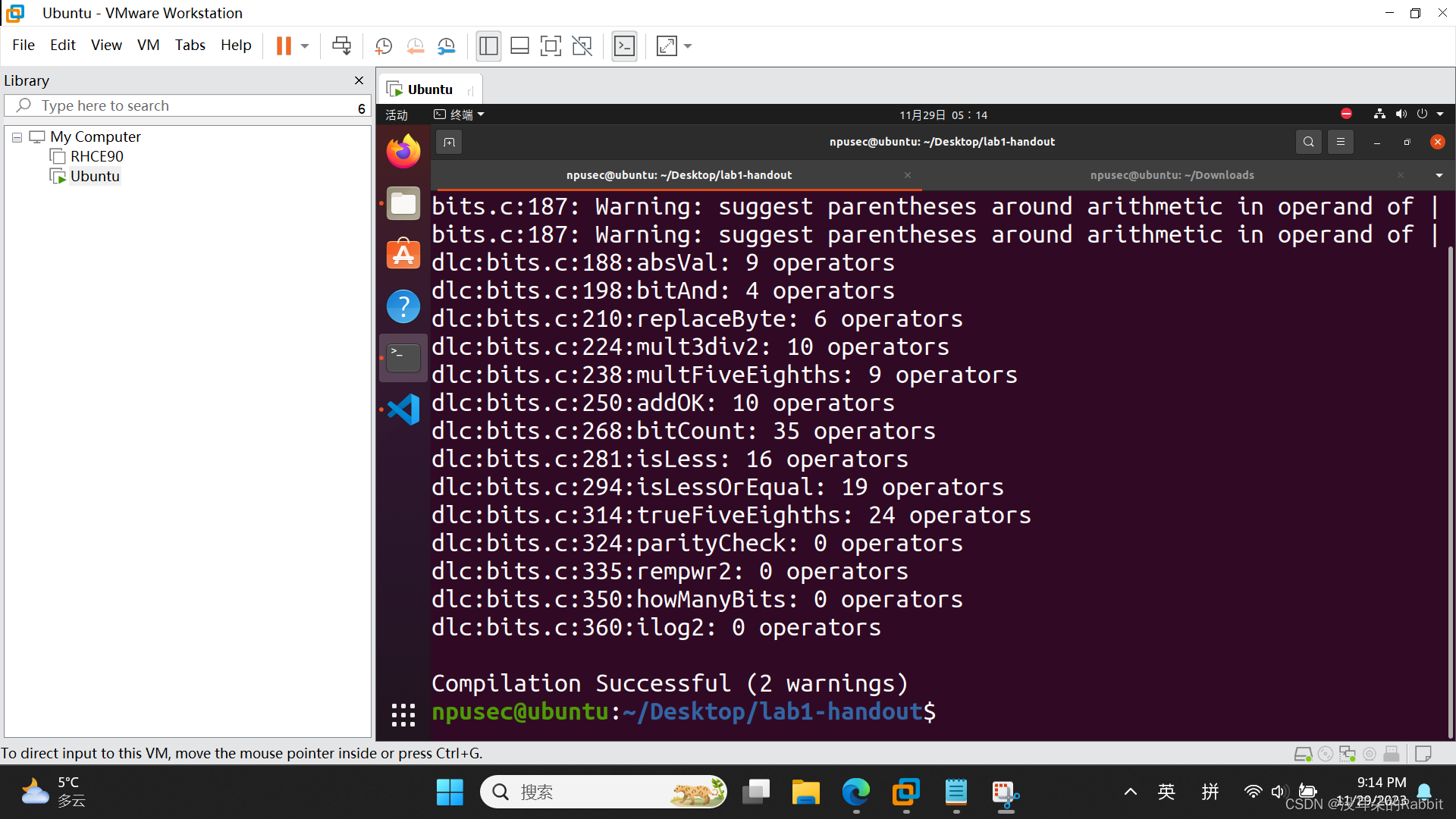
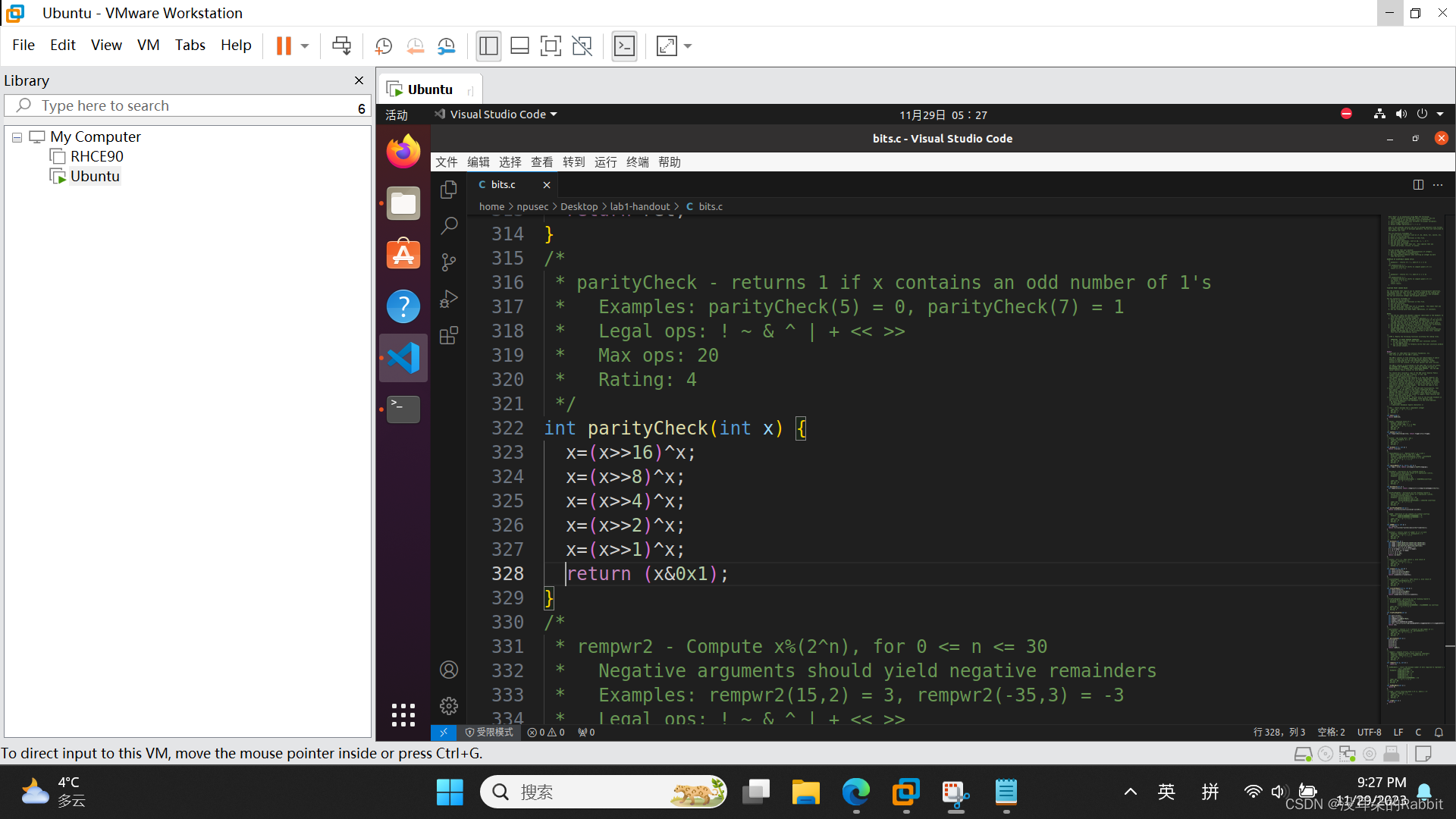
最后看第13个函数,int rempwr2(int x, int n),要求我们计算x%(2^n),其中0<=n<=30。该怎么做呢?我们来看,如果x=0x12345678,n=16,那么x%(2^n)的结果即为0x5678;如果x=0x12345678,n=8,那么x%(2^n)的结果即为0x78;如果x=0x12345678,n=24,那么x%(2^n)的结果即为0x345678。看到这儿,相信大家已经有了思路,即首先针对不同的n,计算出相应的掩码(你不需要知道掩码具体是干嘛的,你只需要知道它是用来获取特定比特位的就行了,大二上计算机网络会详细讲到),可以写作"int mask=~((0x1<<31)>>(32+~n+1));",接着"return x&mask"即可,但是注意!!!这仅适用于x为正数的情况,如果x为负数,比如x=0x80000001,n=8,那么x%(2^n)的结果不应该为0x01,而应该是0xFFFFFF01;比如x=0x80000002,n=8,那么x%(2^n)的结果不应该为0x02,而应该是0xFFFFFF02;比如x=0xFFFFFFFF,n=8,那么x%(2^n)的结果不应该为0xFF,而应该是0xFFFFFFFF,即需要在x&mask的基础上,在填充相应的几个F,即"(x&mask)&((0x1<<31)>>31)"(说实话我们的这个方法很蹩脚,很不推荐使用)。另外如果n=0,则应该返回0,如(图7:第13个函数)所示。(对不起大家哈,中间省略了很多很多的调试步骤,没有展示出来)
**************************************************************************************************************
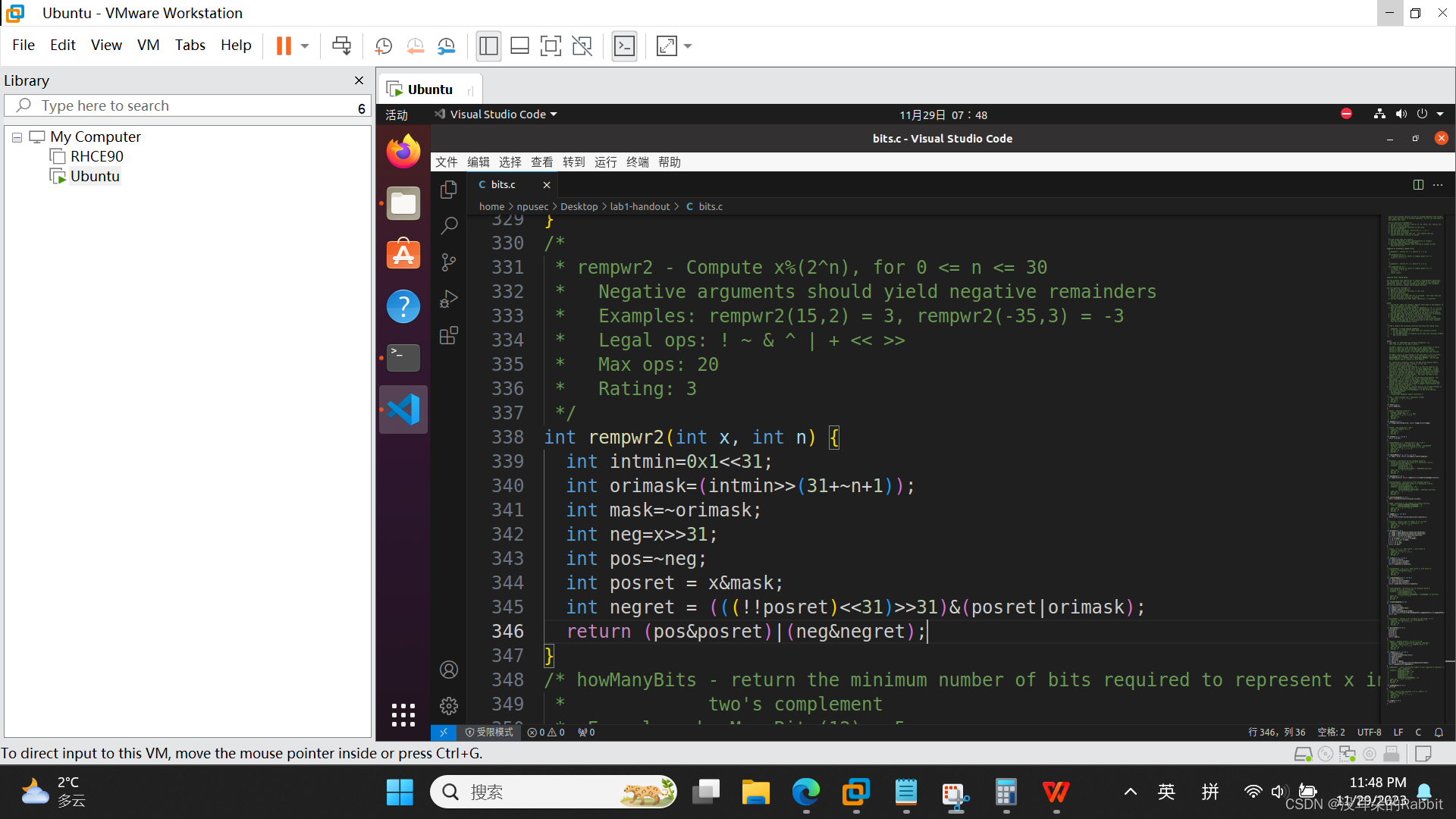


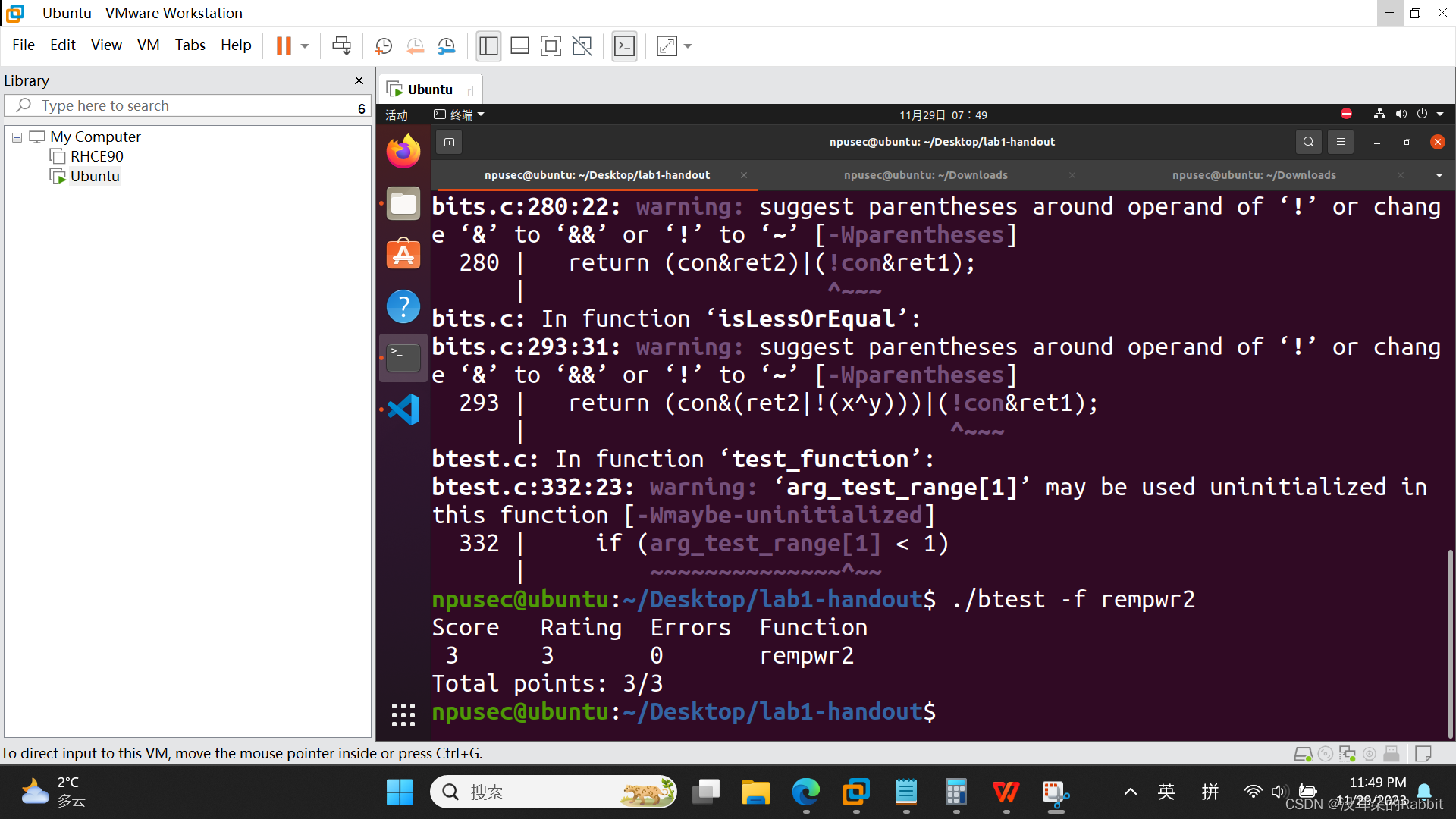
(图7:第13个函数)
**************************************************************************************************************
最后,这5个函数的C语言源代码如(图8:第9,10,11,12,13个函数的C语言源代码)所示。同时再一次告诉大家,不要被做得快的人搞崩了心态,一步一步慢慢来,基础打好了,未来什么都不怕。加油!
**************************************************************************************************************
int isLess(int x, int y) {
int ret1=~(x>>31)+1;
int ret2=((x+~y+1)>>31)&0x1;
int con=!((x>>31)^(y>>31));
return (con&ret2)|(!con&ret1);
}
int isLessOrEqual(int x, int y) {
int ret1=~(x>>31)+1;
int ret2=((x+~y+1)>>31)&0x1;
int con=!((x>>31)^(y>>31));
return (con&(ret2|!(x^y)))|(!con&ret1);
}
int trueFiveEighths(int x)
{
int pos=!(x>>31);
int neg=1+~(x>>31);
int end57df=!((x&0x5)^0x5);
int end08=!(x&0x7);
int endother=(!end57df)&(!end08);
int ret = (x>>1)+(x>>3)+(1&((pos&end57df)|(neg&endother)))+((neg&end57df)<<1);
return ret;
}
int parityCheck(int x) {
x=(x>>16)^x;
x=(x>>8)^x;
x=(x>>4)^x;
x=(x>>2)^x;
x=(x>>1)^x;
return (x&0x1);
}
int rempwr2(int x, int n) {
int intmin=0x1<<31;
int orimask=(intmin>>(31+~n+1));
int mask=~orimask;
int neg=x>>31;
int pos=~neg;
int posret = x&mask;
int negret = (((!!posret)<<31)>>31)&(posret|orimask);
return (pos&posret)|(neg&negret);
}(图8:第9,10,11,12,13个函数的C语言源代码)
**************************************************************************************************************