矩阵快速幂及应用实战[C/C++]

news2025/1/20 1:54:07

矩阵快速幂

矩阵快速幂可以用来优化递推问题，如状态机DP，需要一丢丢线性代数里面矩阵的概念，只需要知道简单的矩阵乘法，结合我们普通的二分快速幂就能很快的掌握矩阵快速幂。

问题引入

三步问题。有个小孩正在上楼梯，楼梯有n阶台阶，小孩一次可以上1阶、2阶或3阶。实现一种方法，计算小孩有多少种上楼梯的方式。结果可能很大，你需要对结果模1000000007。

对于这种递推入门题目，相信只要对于编程有着一定了解的人都能够很快的解决掉。

假如我们用传统递推
f ( 0 ) = 1 , f ( 1 ) = 1 , f ( 2 ) = 2 f ( n ) = f ( n − 1 ) + f ( n − 2 ) + f ( n − 3 ) \begin{array}{c} f(0) = 1 , f(1) = 1 , f(2) = 2\\ f(n) = f(n-1) + f(n - 2) + f(n - 3) \end{array} f(0)=1,f(1)=1,f(2)=2f(n)=f(n−1)+f(n−2)+f(n−3)​

const int MOD = 1e9 + 7;
int dp[1000001];
    int waysToStep(int n) {
        memset(dp , 0 , sizeof(dp));
        dp[0] = 1, dp[1] = 1 , dp[2] = 2;
        for(int i = 3 ; i <= n ; i++)
        dp[i] = ((long long)dp[i - 3] + dp[i - 2] + dp[i - 1]) % MOD;
        return dp[n];
    }

时间复杂度：O(N) 空间复杂度：O(N)

因为每次状态都由前三个状态转移过来，如果用滚动数组优化

const int MOD = 1e9 + 7;
    int waysToStep(int n) {
        int dp0 = 1, dp1 = 1 , dp2 = 2;
        if(n <= 1) return 1;
        if(n == 2) return 2;
        for(int i = 3 ; i <= n ; i++)
        {
        int newdp = ((long long)dp0 + dp1 + dp2) % MOD;
        dp0 = dp1 , dp1 = dp2 , dp2 = newdp;
        }
        return dp2;
    }

空间复杂度优化到了O(1)，时间复杂度仍为O(N)

到滚动数组优化这一步对于大多数初学者来说已经很不错了，如果我们想更进一步呢？

我们重新分析递推公式
f ( 0 ) = 1 , f ( 1 ) = 1 , f ( 2 ) = 2 f ( n ) = f ( n − 1 ) + f ( n − 2 ) + f ( n − 3 ) \begin{array}{c} f(0) = 1 , f(1) = 1 , f(2) = 2\\ f(n) = f(n-1) + f(n - 2) + f(n - 3) \end{array} f(0)=1,f(1)=1,f(2)=2f(n)=f(n−1)+f(n−2)+f(n−3)​

递推公式到向量计算

第一步

我们尝试把递推公式写成矩阵乘上一个列向量的形式，如下：

( f ( n ) ? ? ) = ( 1 1 1 ? ? ? ? ? ? ) ( f ( n − 1 ) f ( n − 2 ) f ( n − 3 ) ) \begin{pmatrix} f(n)\\ ?\\ ? \end{pmatrix} =\begin{pmatrix} 1 & 1 & 1 \\ ? & ? & ? \\ ? & ? & ? \end{pmatrix} \begin{pmatrix} f(n - 1)\\ f(n - 2) \\ f(n - 3) \end{pmatrix} ​f(n)??​ ​= ​1??​1??​1??​ ​ ​f(n−1)f(n−2)f(n−3)​ ​

第二步

接着尝试填充？部分

( f ( n ) f ( n − 1 ) f ( n − 2 ) ) = ( 1 1 1 ? ? ? ? ? ? ) ( f ( n − 1 ) f ( n − 2 ) f ( n − 3 ) ) \begin{pmatrix} f(n)\\ f(n - 1)\\ f(n - 2) \end{pmatrix} =\begin{pmatrix} 1 & 1 & 1 \\ ? & ? & ? \\ ? & ? & ? \end{pmatrix} \begin{pmatrix} f(n - 1)\\ f(n - 2) \\ f(n - 3) \end{pmatrix} ​f(n)f(n−1)f(n−2)​ ​= ​1??​1??​1??​ ​ ​f(n−1)f(n−2)f(n−3)​ ​

第三步

补充矩阵中的部分，就得到了：

( f ( n ) f ( n − 1 ) f ( n − 2 ) ) = ( 1 1 1 1 0 0 0 1 0 ) ( f ( n − 1 ) f ( n − 2 ) f ( n − 3 ) ) \begin{pmatrix} f(n)\\ f(n - 1)\\ f(n - 2) \end{pmatrix} =\begin{pmatrix} 1 & 1 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{pmatrix} \begin{pmatrix} f(n - 1)\\ f(n - 2) \\ f(n - 3) \end{pmatrix} ​f(n)f(n−1)f(n−2)​ ​= ​110​101​100​ ​ ​f(n−1)f(n−2)f(n−3)​ ​

第四步

你以为到这里就结束了？我们在该式子的基础上带入n - 1作为变量，则有：

( f ( n − 1 ) f ( n − 2 ) f ( n − 3 ) ) = ( 1 1 1 1 0 0 0 1 0 ) ( f ( n − 2 ) f ( n − 3 ) f ( n − 4 ) ) \begin{pmatrix} f(n - 1)\\ f(n - 2)\\ f(n - 3) \end{pmatrix} =\begin{pmatrix} 1 & 1 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{pmatrix} \begin{pmatrix} f(n - 2)\\ f(n - 3) \\ f(n - 4) \end{pmatrix} ​f(n−1)f(n−2)f(n−3)​ ​= ​110​101​100​ ​ ​f(n−2)f(n−3)f(n−4)​ ​

第五步

我们把第四步中的式子带入到第三步中，就会得到

( f ( n ) f ( n − 1 ) f ( n − 2 ) ) = ( 1 1 1 1 0 0 0 1 0 ) ( 1 1 1 1 0 0 0 1 0 ) ( f ( n − 2 ) f ( n − 3 ) f ( n − 4 ) ) \begin{pmatrix} f(n)\\ f(n - 1)\\ f(n - 2) \end{pmatrix} =\begin{pmatrix} 1 & 1 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{pmatrix} \begin{pmatrix} 1 & 1 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{pmatrix} \begin{pmatrix} f(n - 2)\\ f(n - 3) \\ f(n - 4) \end{pmatrix} ​f(n)f(n−1)f(n−2)​ ​= ​110​101​100​ ​ ​110​101​100​ ​ ​f(n−2)f(n−3)f(n−4)​ ​

第六步

我们不断地迭代下去就会有这样一个式子：

( f ( n ) f ( n − 1 ) f ( n − 2 ) ) = ( 1 1 1 1 0 0 0 1 0 ) n − 2 ( f ( 2 ) f ( 1 ) f ( 0 ) ) \begin{pmatrix} f(n)\\ f(n - 1)\\ f(n - 2) \end{pmatrix} =\begin{pmatrix} 1 & 1 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{pmatrix}^{n-2} \begin{pmatrix} f(2)\\ f(1) \\ f(0) \end{pmatrix} ​f(n)f(n−1)f(n−2)​ ​= ​110​101​100​ ​n−2 ​f(2)f(1)f(0)​ ​
我们发现f(n)的计算还可以通过计算出一个已知矩阵的n - 2次幂与一个列向量的乘积来获取。那么这样的计算方式可以令我们算法的执行效率得到提高吗？

对于两个M阶矩阵做乘积，其时间复杂度为O(M^3)，进行n - 2次，那么时间复杂度就是O(M^3 * n)，似乎与我们的传统递归相比还要慢上常数阶，于是这就引出了我们今天的主题矩阵快速幂

普通二分快速幂

关于二分快速幂的介绍在笔者的另一篇博客有详细介绍及证明二分快速幂和快读快写模板【C++】-CSDN博客

对于我们快速求a ^ b % p，我们可以不断地二分为(a ^ 2) ^ (b / 2) % p…

如果出现b为奇数，就使得我们最终的返回值ans（ans初始为1）乘上a，当指数为0的时候循环执行完毕，此时ans就是我们的答案。

同样的思想也可以用于矩阵的幂运算中。

代码如下

inline long long quickPower(int a, int b, int p)
{
    long long ans = 1;
    while (b)
    {
        if (b & 1)
        {
            ans = ans * a % p;
        }
        a = a * a % p;
        b /= 2;
    }
    return ans;
}

矩阵二分快速幂

由普通二分快速幂对矩阵做推广，可有如下递归式
A n = { I                       n = 0 ( A n − 1 2 ) 2 × A         n 为奇数 ( A n 2 ) 2 × A                   n 为非零偶数 A^{n} = \left\{\begin{matrix} I\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ n=0 \\ (A^{\frac{n-1}{2}})^2\times A \ \ \ \ \ \ \ n为奇数 \\ (A^{\frac{n}{2}})^2\times A \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ n为非零偶数 \\ \end{matrix}\right. An=⎩ ⎨ ⎧​I                     n=0(A2n−1​)2×A       n为奇数(A2n​)2×A                 n为非零偶数​
那么我们只需要把普通二分快速幂模板中整数乘法更换成矩阵乘法即可。

矩阵类的定义

struct Matrix
{
    int m[101][101];

    Matrix()
    {
        memset(m, 0, sizeof(m));
    }
};

矩阵乘法的运算符重载

Matrix operator*(const Matrix &x, const Matrix &y)
{
    Matrix ret;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= n; j++)
            for (int k = 1; k <= n; k++)
                ret.m[i][j] = (ret.m[i][j] + (x.m[i][k] * y.m[k][j]) % MOD) % MOD;
    return ret;
}

矩阵快速幂模板

Matrix MatrixQuickPower(const Matrix &A, int k)
{
    Matrix res;
    for (int i = 1; i <= n; i++)
        res.m[i][i] = 1; // 单位矩阵
    while (k)
    {
        if (k & 1)
            res = res * A;
        A = A * A;
        k >>= 1;
    }
    return res;
}

矩阵快速幂就是对普通二分快速幂的基础上，将运算对象更改为了矩阵罢了。

矩阵乘法的常数级优化

我们发现矩阵乘法这里y每次访问m[k][j]寻址需要跳过一整行，对性能其实是有一定影响的，我们可以把第二层循环和第三层循环进行交换

Matrix operator*(const Matrix &x, const Matrix &y)
{
    Matrix ret;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= n; j++)
            for (int k = 1; k <= n; k++)
                ret.m[i][j] = (ret.m[i][j] + (x.m[i][k] * y.m[k][j]) % MOD) % MOD;
    return ret;
}

则有

Matrix operator*(const Matrix &x, const Matrix &y)
{
    Matrix ret;
    for (int i = 1; i <= n; i++)
        for (int k = 1; k <= n; k++)
            for (int j = 1; j <= n; j++)
                ret.m[i][j] = (ret.m[i][j] + (x.m[i][k] * y.m[k][j]) % MOD) % MOD;
    return ret;
}

这样既不影响结果，又降低了寻址消耗。

矩阵快速幂在状态机DP中的应用

如果你学习过数字逻辑电路，相信对于时序电路中的有限状态机不会陌生，没有学过也没有关系，因为学了也不会状态机DP，做算法题早晚都要面对的

其实虽然状态机DP在动态规划中算是一类难度不低的问题，但是只要多做几道题就会很快的掌握其套路，相较于背包问题，难度低了不少，因为套路更容易掌握。

下面详解一道题，留下另一道题供读者练手。

OJ题目精讲

935. 骑士拨号器

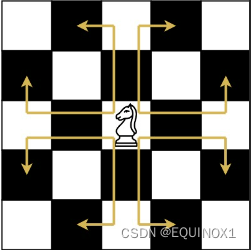
象棋骑士有一个独特的移动方式，它可以垂直移动两个方格，水平移动一个方格，或者水平移动两个方格，垂直移动一个方格(两者都形成一个 L 的形状)。

象棋骑士可能的移动方式如下图所示:

外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

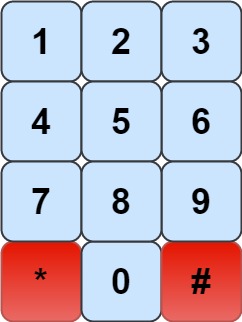
我们有一个象棋骑士和一个电话垫，如下所示，骑士只能站在一个数字单元格上(即蓝色单元格)。

img

给定一个整数 n，返回我们可以拨多少个长度为 n 的不同电话号码。

你可以将骑士放置在任何数字单元格上，然后你应该执行 n - 1 次移动来获得长度为 n 的号码。所有的跳跃应该是有效的骑士跳跃。

因为答案可能很大，所以输出答案模 109 + 7.

对于长度为n的电话号码，每个位置有10种情况，如果没有题目中的限制，我们通过简单的组合数学就可以解决.

但现在每个位置可以移动的方式都给出了限制,也就是说在每个位置可以抵达的下一个位置是确定且有限的.

我们如果把每个位置都看做成是一种状态，那么我们有如下的状态转移关系：

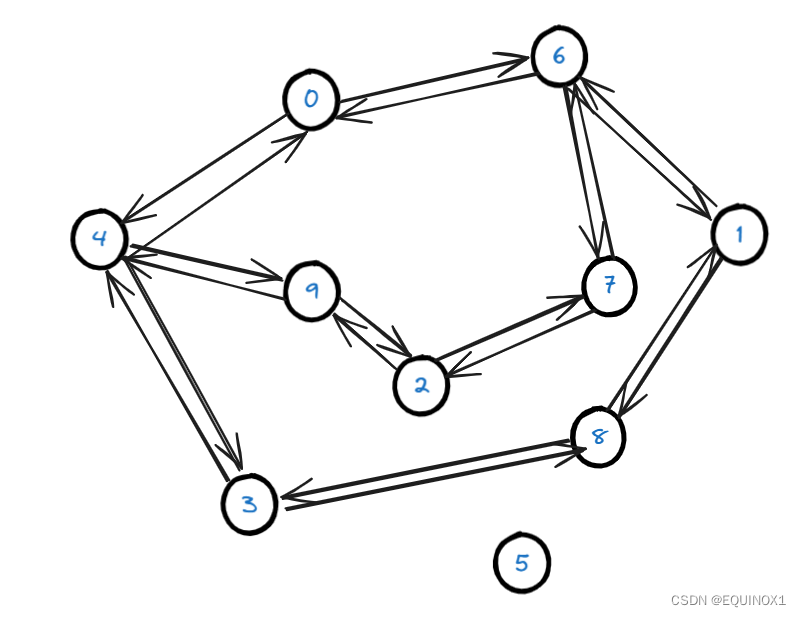
外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

我们定义状态dp[i][j]为第i次移动后在位置j的情况数，那么我们有如下状态转移方程：
d p [ i ] [ j ] = ∑ d p [ i − 1 ] [ k ] , 其中 j 可由 k 转移 dp[i][j] = \sum dp[i-1][k],其中j可由k转移 dp[i][j]=∑dp[i−1][k],其中j可由k转移

非矩阵快速幂解法

我们打表列出每个位置的的前驱状态，然后执行状态转移方程，最后对dp[n][i]进行累加即可

class Solution {
public:
const int MOD = 1e9 + 7;
vector<vector<int>> pre{
    {4 , 6} , {6 , 8} , {7 , 9} , {4 , 8} , {0 , 3 , 9} , {} , {0 , 1 , 7} , {2 , 6} , {1 , 3} , {2 , 4}
};
    int knightDialer(int n) {
        vector<vector<int>> dp(n + 1 , vector<int>(10));
        for(int i = 0 ; i < 10 ; i++)
        dp[1][i] = 1;
        for(int i = 2 ; i <= n ; i++)
        {
            for(int j = 0 ; j < 10 ; j++)
            {
                for(auto x : pre[j])
                dp[i][j] = (dp[i - 1][x] + dp[i][j]) % MOD; 
            }
        }
        long long ret = 0;
        for(int i = 0 ; i < 10 ; i++)
        ret = (ret + dp[n][i]) % MOD;
        return ret;
    }
};
滚动数组优化

由于每个状态只与上一次状态有关，所以我们还可以优化二维为一维，代码如下：

class Solution {
public:
const int MOD = 1e9 + 7;
vector<vector<int>> pre{
    {4 , 6} , {6 , 8} , {7 , 9} , {4 , 8} , {0 , 3 , 9} , {} , {0 , 1 , 7} , {2 , 6} , {1 , 3} , {2 , 4}
};
    int knightDialer(int n) {
        vector<int> dp(10);
        for(int i = 0 ; i < 10 ; i++)
        dp[i] = 1;
        for(int i = 2 ; i <= n ; i++)
        {
            vector<int> newdp(10);
            for(int j = 0 ; j < 10 ; j++)
            {
                for(auto x : pre[j])
                newdp[j] = (dp[x] + newdp[j]) % MOD; 
            }
            dp = newdp;
        }
        long long ret = 0;
        for(int i = 0 ; i < 10 ; i++)
        ret = (ret + dp[i]) % MOD;
        return ret;
    }
};
矩阵快速幂解法

其实我们对于我们矩阵快速幂优化递推问题而言，只要提前写出矩阵A的行列式即可。对于本题我们分析
n e w d p [ 0 ] = d p [ 4 ] + d p [ 6 ] n e w d p [ 1 ] = d p [ 6 ] + d p [ 8 ] n e w d p [ 2 ] = d p [ 7 ] + d p [ 9 ] . . . \begin{array}{c} newdp[0] = dp[4]+dp[6]\\ newdp[1] = dp[6]+dp[8]\\ newdp[2] = dp[7]+dp[9]\\ ... \end{array} newdp[0]=dp[4]+dp[6]newdp[1]=dp[6]+dp[8]newdp[2]=dp[7]+dp[9]...​
对于我们的10x10矩阵A的行列式可以很容易的计算出，于是我们的递推公式的矩阵表示为：
$$
\begin{pmatrix}
dpn(0)\
dpn(1)\
dpn(2)\
dpn(3)\
dpn(4)\
dpn(5)\
dpn(6)\
dpn(7)\
dpn(8)\
dpn(9)
\end{pmatrix} =\begin{pmatrix}
{0, 0, 0, 0, 1, 0, 1, 0, 0, 0}\
{0, 0, 0, 0, 0, 0, 1, 0, 1, 0}\
{0, 0, 0, 0, 0, 0, 0, 1, 0, 1}\
{0, 0, 0, 0, 1, 0, 0, 0, 1, 0}\
{1, 0, 0, 1, 0, 0, 0, 0, 0, 1}\
{0, 0, 0, 0, 0, 0, 0, 0, 0, 0}\
{1, 1, 0, 0, 0, 0, 0, 1, 0, 0}\
{0, 0, 1, 0, 0, 0, 1, 0, 0, 0}\
{0, 1, 0, 1, 0, 0, 0, 0, 0, 0}\
{0, 0, 1, 0, 1, 0, 0, 0, 0, 0}

\end{pmatrix}^{n} \begin{pmatrix}
dp(0)\
dp(1)\
dp(2)\
dp(3)\
dp(4)\
dp(5)\
dp(6)\
dp(7)\
dp(8)\
dp(9)
\end{pmatrix}
$$
我们矩阵运算时间复杂度为O(103)，执行logn次，这样我们的时间复杂度就降到了**O(103 * logn)**

代码如下：

const int MOD = 1e9 + 7;

struct Matrix
{
	long long m[10][10];

	Matrix()
	{
		memset(m, 0, sizeof(m));
	}
	Matrix(int x) :m{
		{0, 0, 0, 0, 1, 0, 1, 0, 0, 0},
		{0, 0, 0, 0, 0, 0, 1, 0, 1, 0},
		{0, 0, 0, 0, 0, 0, 0, 1, 0, 1},
		{0, 0, 0, 0, 1, 0, 0, 0, 1, 0},
		{1, 0, 0, 1, 0, 0, 0, 0, 0, 1},
		{0, 0, 0, 0, 0, 0, 0, 0, 0, 0},
		{1, 1, 0, 0, 0, 0, 0, 1, 0, 0},
		{0, 0, 1, 0, 0, 0, 1, 0, 0, 0},
		{0, 1, 0, 1, 0, 0, 0, 0, 0, 0},
		{0, 0, 1, 0, 1, 0, 0, 0, 0, 0}
	}
	{}
};
Matrix A, dp;

Matrix operator*(const Matrix& x, const Matrix& y)
{
	Matrix ret;
	for (int i = 0; i < 10; i++)
		for (int k = 0; k < 10; k++)
			for (int j = 0; j < 10; j++)
				ret.m[i][j] = (ret.m[i][j] + (x.m[i][k] * y.m[k][j]) % MOD) % MOD;
	return ret;
}
Matrix MatrixQuickPower(Matrix& A, int k)
{
	Matrix res;
	for (int i = 0; i < 10; i++)
		res.m[i][i] = 1; // 单位矩阵
	while (k)
	{
		if (k & 1)
			res = res * A;
		A = A * A;
		k >>= 1;
	}
	return res;
}
int init(int n)
{
	A = Matrix(1);
	for (int i = 0; i < 10; i++)
		dp.m[i][0] = 1;
	Matrix dpn = MatrixQuickPower(A, n - 1) * dp;
	int ret = 0;
	for (int i = 0; i < 10; i++)
		ret = (ret + dpn.m[i][0]) % MOD;
	return ret;
}
class Solution {
public:
	int knightDialer(int n) {
		return init(n);
	}
};

外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

遥遥领先

这里省事直接套模板了，有很多拷贝是可以优化掉的。就不演示了（懒x_x）

练习题OJ链接

这道题留给大家练习

552. 学生出勤记录 II - 力扣（LeetCode）

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1269200.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

什么是海外私人IP代理?是纯净独享的代理吗？

什么是海外私人IP代理?是纯净独享的代理吗？

相信许多互联网工作者都遇到过IP禁令&#xff0c;比如网络抓取项目&#xff0c;使用共享代理服务器向网站发出第一个请求&#xff0c;但却您收到了禁令&#xff0c;这大部分是由于你的共享IP经过多人使用被禁用所致。 那么到底什么是私人代理呢&#xff1f;它们是否适合您的情…
阅读更多...
【刷题】链表

【刷题】链表

链表 206. 反转链表 给你单链表的头节点 head &#xff0c;请你反转链表&#xff0c;并返回反转后的链表。 示例 1&#xff1a; 输入&#xff1a;head [1,2,3,4,5] 输出&#xff1a;[5,4,3,2,1] 示例 2&#xff1a; 输入&#xff1a;head [1,2] 输出&#xff1a;[2,1] 示…
阅读更多...
进程间通信基础知识【Linux】——上篇

进程间通信基础知识【Linux】——上篇

目录 一&#xff0c;理解进程之间的通信 1. 进程间通信目的 2. 进程间通信的技术背景 3&#xff0c;常见的进程间通信 二&#xff0c;管道 1. 尝试建立一个管道 管道的特点&#xff1a; 管道提供的访问控制&#xff1a; 2. 扩展&#xff1a;进程池 阶段一&#xff1a…
阅读更多...
Motion Plan之带动力学约束路径搜索

Motion Plan之带动力学约束路径搜索

Motion Plan之搜索算法笔记 Motion Plan之基于采样的路径规划算法笔记 为什么要动力学规划&#xff1a; 前面几章介绍的路径规划&#xff0c;我们只是认为机器人是质点&#xff0c;这节课要说的就是&#xff0c;如何在考虑机器人的运动学模型下再去找一个安全可行的路径。考虑…
阅读更多...
如何缓解可观察性挑战？

如何缓解可观察性挑战？

可观察性正在成为当代 DevOps 实践的基石。即使传统上不属于 DevOps 的部门也看到了在可观察性团队的支持下带来的好处。然而&#xff0c;到 2023 年&#xff0c;组织发现采用之路比预期更加崎岖。以下是 DevOps 团队在可观察性方面面临的七个最大挑战以及一些缓解这些挑战的建…
阅读更多...
消息中间件——RabbitMQ（七）高级特性 2

消息中间件——RabbitMQ（七）高级特性 2

前言 上一篇消息中间件——RabbitMQ&#xff08;七&#xff09;高级特性 1中我们介绍了消息如何保障100%的投递成功&#xff1f;,幂等性概念详解,在海量订单产生的业务高峰期&#xff0c;如何避免消息的重复消费的问题&#xff1f;,Confirm确认消息、Return返回消息。这篇我们…
阅读更多...
hive里如何高效生成唯一ID

hive里如何高效生成唯一ID

常见的方式&#xff1a; hive里最常用的方式生成唯一id&#xff0c;就是直接使用 row_number() 来进行&#xff0c;这个对于小数据量是ok的&#xff0c;但是当数据量大的时候会导致&#xff0c;数据倾斜&#xff0c;因为最后生成全局唯一id的时候&#xff0c;这个任务是放在一个…
阅读更多...
Linux 进程(二)

Linux 进程(二)

1.当前工作目录 Linux 下使用 ls /proc 查看程序中的进程&#xff0c;其中这些蓝色的数字代表的就是进程。 其中cwd(current working directory)就是当前工作目录&#xff0c;那么为什么cwd 和 exe 是在同一级目录下呢因为 进程需要依赖可执行程序&#xff0c;可执行程序需要依…
阅读更多...
局部内部类(内部类) - Java

局部内部类(内部类) - Java

局部内部类 说明&#xff1a;局部内部类是定义在外部类的局部位置&#xff0c;比如方法中&#xff0c;并且有类名。 LocalInnerClass.java 非常重要的几点&#xff01;&#xff01; 局部内部类本质还是一个类&#xff0c;该有的属性方法也都可以有。【举例a.见下文】可以直接…
阅读更多...
KT1404C语音芯片为什么用着用着，声音就变大了，发指令设置音量？

KT1404C语音芯片为什么用着用着，声音就变大了，发指令设置音量？

一、问题简介 有客户反馈&#xff0c;使用KT404C语音芯片&#xff0c;每次主板上电的时候&#xff0c;都会发指令将音量设置为20级&#xff0c;但是实际到使用现场&#xff0c;就会有终端的客人反馈&#xff0c;机器的音量变大了&#xff0c;这个是什么情况呢&#xff0c;该如…
阅读更多...
微服务API网关Spring Cloud Gateway实战

微服务API网关Spring Cloud Gateway实战

概述 微服务网关是为了给不同的微服务提供统一的前置功能&#xff1b;网关服务可以配置集群&#xff0c;以承载更多的流量&#xff1b;负载均衡与网关互相成就&#xff0c;一般使用负载均衡&#xff08;例如 nginx&#xff09;作为总入口&#xff0c;然后将流量分发到多个网关…
阅读更多...
远程办公和密码管理的好伴侣

远程办公和密码管理的好伴侣

在当今快速变化的商业环境中&#xff0c;远程办公已经不再是一种简单的应急措施&#xff0c;而是被视为企业长期发展的关键战略之一。 随着科技的不断进步和全球化的推动&#xff0c;远程办公为企业提供了更大的灵活性和适应性&#xff0c;使得员工能够更好地平衡工作和生活。这…
阅读更多...
ardupilot开发 --- ROS 篇

ardupilot开发 --- ROS 篇

0. 前言 关于机载计算机&#xff1b; 关于ROS; 关于基于ROS的视觉SLAM和避障&#xff1b; 1. APSync 说到机载计算机Companion computer就不得不提另一个关键词APSync&#xff1b;APSync简化了机载计算机的设置&#xff0c;以便它可以为ArduPilot提供额外的功能&#xff0c;…
阅读更多...
Debian arm系统安装wxPython

Debian arm系统安装wxPython

一、系统版本 二、安装wxPython-4.0.4.tar.gz 1、下载依赖 >sudo apt update >sudo apt-get install build-essential libgtk-3-dev libwebkit2gtk-4.0-dev libssl-dev libcurl4-openssl-dev libgstreamer-plugins-base1.0-dev libnotify-dev freeglut3 freeglut3-dev …
阅读更多...
Python爬虫遇到重定向URL问题时如何解决？

Python爬虫遇到重定向URL问题时如何解决？

什么是重定向 重定向是指当用户请求一个URL时&#xff0c;服务器返回一个中断请求的URL的响应。这种情况通常发生在网站对URL进行了修改或者重定向到其他页面的情况下。其中&#xff0c;如果处理不当开发&#xff0c;可能会导致爬虫无法获取所需的数据&#xff0c;从而影响爬虫…
阅读更多...
激光切割机切割工件出现锯齿是什么原因？

激光切割机切割工件出现锯齿是什么原因？

金属激光切割机因切割速度快&#xff0c;效率高&#xff0c;切割效果好受到广大金属加工需求的厂家追捧&#xff0c;但在使用时不免出现一些小问题&#xff0c;如&#xff1a;在激光切割加工的时候出现锯齿的问题。 编辑搜图 请点击输入图片描述&#xff08;最多18字&#xff…
阅读更多...
传感器：探索Android中的传感器功能与使用

传感器：探索Android中的传感器功能与使用

传感器&#xff1a;探索Android中的传感器功能与使用 一、传感器介绍1.1 Android 平台三大类传感器1.2 Android 平台支持的传感器1.3 传感器框架 二、传感器的使用2.1 识别传感器和传感器特性2.2 针对不同制造商的传感器或传感器的不同版本优化2.3 监控传感器事件2.4 处理不同的…
阅读更多...
Docker中Alpine容器中配置MariaDB

Docker中Alpine容器中配置MariaDB

1.更新镜像源 apk update2.安装 Mysql apk add --no-cache mysql mysql-client # 安装命令也可使用 apk add mariadb mariadb-client&#xff0c;alpine 中 mysql 就是 mariadb3. 安装openrc openrc是Alpine服务控制器&#xff0c;负责Alpine服务启动&#xff0c;添加、删除…
阅读更多...
Linux 基本语句_13_消息队列

Linux 基本语句_13_消息队列

概念&#xff1a; 不同进程能通过消息队列来进行通信&#xff0c;不同进程也能获取或发送特定类型的消息&#xff0c;即选择性的收发消息。 一般一个程序采取子进程发消息&#xff0c;父进程收消息的模式 常用函数功能&#xff1a; fork(); // 创建子进程 struct msgbuf{ …
阅读更多...
探索测试开发工程师的通往成功的秘密路径！

探索测试开发工程师的通往成功的秘密路径！

「作者说」随着近几年国内IT行业高速发展&#xff0c;对测试工程师的要求也越来越高&#xff0c;其作用也越来越重要&#xff0c;但很多测试工程师也迎来了个人发展的瓶颈&#xff0c;下一步该向哪个方向发展&#xff0c;该如何发展&#xff1f;本文将概述测试工程师的现状及发…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023