编者按：

住院流程（Inpatient Flow）是一种通过协调和优化医院内部流程，以提高患者入院至出院期间的效率和质量的方法。住院流程通常通过医院内部信息系统和协同工作流程进行管理，以确保患者得到及时的诊断、治疗和护理。办理住院的病人主要有以下几个渠道来源： （1）预约住院（2）非预约住院（3）病人转院。

住院流程优化问题往往涉及包括床位分配，预约住院病人分配，急诊病人分配等一系列问题。考虑到问题的复杂性， 近年来住院流程优化在医疗优化领域备受关注。与上一期不同，本期涉及到的论文主要分别医院床位管理这个小的主题。

1. Meng, Fanwen, et al. “A robust optimization model for managing elective admission in a public hospital.” Operations https://doi.org/10.1287/opre.2015.1423
2. Xie, Jingui, et al. “The analytics of bed shortages: Coherent metric, prediction, and optimization.” Operations Research 71.1 (2023): 23-46. https://doi.org/10.1287/opre.2021.2231

A robust optimization model for managing elective admission in a public hospital.

https://doi.org/10.1287/opre.2015.1423

Problem

医院紧急住院病人的到来往往是紧急的,未经计划的并且优先级较高（需要尽快入院），这对医院的床位安排调度有很大影响。考虑到医院床位资源的稀缺性，（在新加坡），医院往往对择期入院采取配额管理来减少床位不足的发生。当紧急入院病人数量较少时，择期入院的床位配额就较高，反之，择期入院的床位配额就较少。本文提出了一个分布式鲁棒优化模型来确定每日择期入院的床位配额。

Method

本文采用分布式鲁棒优化建立了一个确定每日择期入院的床位配额的混合整数规划模型。 模型的决策变量是床位配额（整数变量）。 考虑到每日住院病人数量的不确定性，作者引入了两个随机变量$\tilde{p}$和 $\tilde{a}$来表示每日紧急（择期）入院的实际病人数量并建立了一个均值支持模糊集 。为了求解这个问题，作者推导得出了一个该模型的二阶锥问题（SOCP）等价形式来解决这个模型。

Summary of results

作者执行了一个时间长度为一年的仿真实验来检测本文提出的优化模型的效果。 下图2表明，相较于确定性的配额策略和均匀分配，使用本文提出的床位分配模型不容易产生床位短缺。

表7给出了本文提出的优化模型相较于确定性的床位配额策略和均匀分配的表现提升。具体来说，在整体床位短缺方面，优化模型相较于确定性配额策略提供了超过24%的改进，而相较于均匀配额策略则提高了53%。

Why recommends?

1. 本文提出了一个分布式鲁棒优化模型用来确定医院的床位配额。具体来说，本文重点关注了病人住院分配问题中的每日优化问题。

2. 与之前的模型中采用的鲁棒优化建模方法不同，本文采用了分布式鲁棒优化的建模方法并在实验中展示了这一建模方法的优越性。

The analytics of bed shortages: Coherent metric, prediction, and optimization

https://doi.org/10.1287/opre.2021.2231

Problem

床位短缺通常对患者满意度和医疗结果产生负面影响。在实践中，医疗管理者通常使用床位占用率（BORs）作为一个度量来了解床位利用情况。 作者提出了床位短缺指数（BSI），用于系统性的度量床位短缺风险。床位短缺指数BSI便于计算，不需要额外的假设或近似。在此基础上，作者还提出了基于BSI规划床位容量的优化模型。 第一个模型在限制BSI的基础上最大化择期住院的床位配额，第二个模型通过最小化稳态BSI来确定最佳的排班策略。

Method

1. 本文基于Aumann and Serrano (2008)提出的风险指数（riskiness index) ,定义了一个床位短缺指数（Bed Shortage Index) 。作者将BSI与其他床位短缺的描述性指标比较并描述了 BSI的性质和实际意义。Theorem 4展示了，在已知医院床位数量$\kappa$，病人到达率$\lambda$和床位配额$\eta$的情况下如何计算BSI.

2. 作者建立了多个模型，使用BSI来度量床位短缺风险并确定床位配额。 模型的决策变量有（1）择期入院的床位配额（2）床位总数的分配（紧急病人/择期入院）（3） 紧急入院病人的到达率。 考虑到的约束条件有：（1）医院的病床数量（2）其他医疗资源的数量限制（3）医疗服务的连续性。

a. 第一个模型的目标函数是最大化择期入院的病人数量（以BSI为约束）。模型可以转化为一个纯线性规划。

b. 第二个模型的目标函数是最小化床位短缺风险。具体来说，作者最小化计划时间范围内的最差BSI.

Summary of results

文中提供了丰富的实践对比结果，笔者在此着重强调以下几个方面：

1. BSI的有效性。下表2展示了根据仿真实验中的实际病床短缺情况计算的BOR和BSI的数值。可以看出BOR和BSI具有一致性。

2. 和排队论模型的对比。本文提出的优化模型允许在病床数量短缺的情况下接受患者，这在本质上其实是一个具有无限资源容量的负载模型。而在传统的排队论模型中，资源数量是有限的，病人在床位已满的情况下必须在队列中等待。 以此为出发点， 作者对比了本文提出的模型和以排队论为基础的床位配额模型。结果表明，同样的实验背景下，排队论模型中， 病床短缺数量的期望值更大（队列期望更大）。这个例子说明，本文提出的模型可能比排队模型更具适用性。

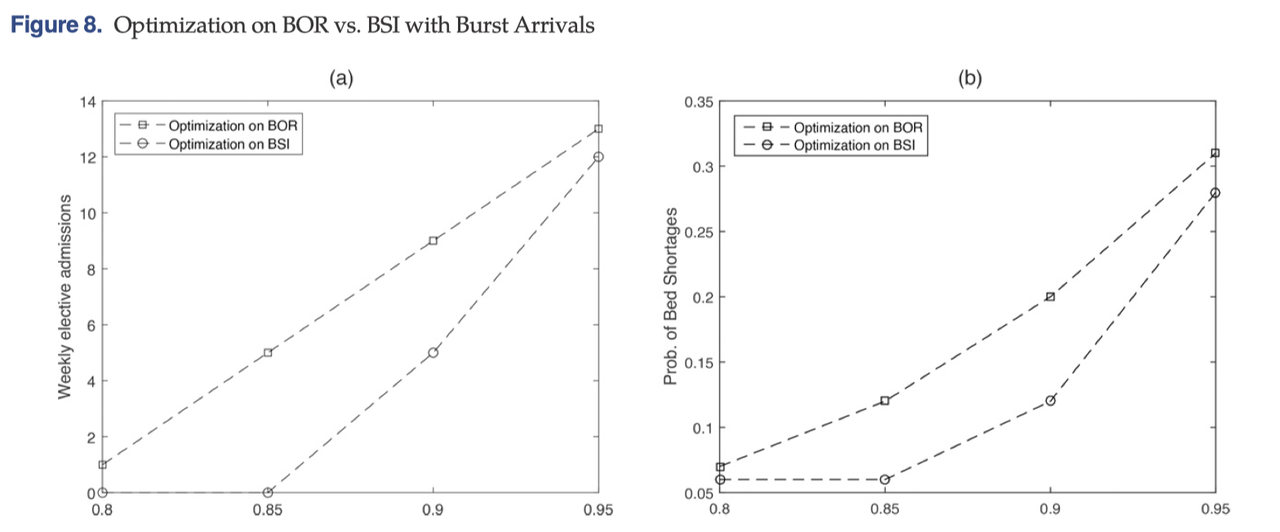
3. BOR和BSI的对比。下图8对比了使用BSI和BOR在优化模型的差异。结果表明，使用BSI，每周择期入院的床位配额数量更少（与理论结果吻合），并且产生床位短缺的风险更低。
   

Why recommends?

1. 文中提出了一个新的病床短缺指标BSI,对这个指标进行了描述并以此为基础建立了优化模型
2. 同样是床位配额问题， 这篇文中提供了与前文不同的视角。

参考文献：

1. Meng, Fanwen, et al. “A robust optimization model for managing elective admission in a public hospital.” Operations

2. Xie, Jingui, et al. “The analytics of bed shortages: Coherent metric, prediction, and optimization.” Operations Research 71.1 (2023): 23-46.