title: Java Integer.toBinaryString() 方法源码及原理解析(进制转换、位运算)
date: 2022-12-27 17:31:38
tags:
- Java
categories: - Java
cover: https://cover.png
feature: false
1. 使用及源码概览
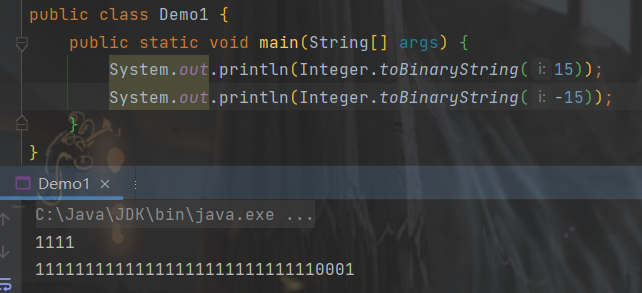
Integer.toBinaryString() 方法用于将十进制整数转为二进制,如下例:
完整源码调用如下:
public static String toBinaryString(int i) {
return toUnsignedString0(i, 1);
}
private static String toUnsignedString0(int val, int shift) {
// assert shift > 0 && shift <=5 : "Illegal shift value";
int mag = Integer.SIZE - Integer.numberOfLeadingZeros(val);
int chars = Math.max(((mag + (shift - 1)) / shift), 1);
char[] buf = new char[chars];
formatUnsignedInt(val, shift, buf, 0, chars);
// Use special constructor which takes over "buf".
return new String(buf, true);
}
public static int numberOfLeadingZeros(int i) {
// HD, Figure 5-6
if (i == 0)
return 32;
int n = 1;
if (i >>> 16 == 0) { n += 16; i <<= 16; }
if (i >>> 24 == 0) { n += 8; i <<= 8; }
if (i >>> 28 == 0) { n += 4; i <<= 4; }
if (i >>> 30 == 0) { n += 2; i <<= 2; }
n -= i >>> 31;
return n;
}
static int formatUnsignedInt(int val, int shift, char[] buf, int offset, int len) {
int charPos = len;
int radix = 1 << shift;
int mask = radix - 1;
do {
buf[offset + --charPos] = Integer.digits[val & mask];
val >>>= shift;
} while (val != 0 && charPos > 0);
return charPos;
}
final static char[] digits = {
'0' , '1' , '2' , '3' , '4' , '5' ,
'6' , '7' , '8' , '9' , 'a' , 'b' ,
'c' , 'd' , 'e' , 'f' , 'g' , 'h' ,
'i' , 'j' , 'k' , 'l' , 'm' , 'n' ,
'o' , 'p' , 'q' , 'r' , 's' , 't' ,
'u' , 'v' , 'w' , 'x' , 'y' , 'z'
};
2. 解析
2.1 二进制转换
首先,从运算逻辑上了解一下怎么从十进制转换为二进制,一般来说有两种方法,这里只用 8 位来做示范
1、短除法
本质上就是不断除 2,直到商为 0 为止,然后将余数倒序输出。例:15,16
2| 15 2| 16
———— ————
2| 7 1 ^ 2| 8 0 ^
———— | ———— |
2| 3 1 | 2| 4 0 |
———— | ———— |
2| 1 1 | 2| 2 0 |
———— | ———— |
0 1 | 2| 1 0 |
———— |
0 1 |
由上,15 的二进制表示为 0000 1111,16 的二进制表示为 0001 0000
2、按权相加法
即将二进制数首先写成加权系数展开式,依次与二进制位对应,然后按十进制加法规则求和
2 的 0 次方是 1 -------------- 对应第 1 位
2 的 1 次方是 2 -------------- 对应第 2 位
2 的 2 次方是 4 -------------- 对应第 3 位
2 的 3 次方是 8 -------------- 对应第 4 位
2 的 4 次方是 16 -------------- 对应第 5 位
2 的 5 次方是 32 -------------- 对应第 6 位
2 的 6 次方是 64 -------------- 对应第 7 位
…
例:15 = 2^3 + 2^2 + 2^1 + 2^0,16 = 2^4,即:
15 16
0000 0000 0000 0000
0000 1000 0001 0000
0000 1100
0000 1110
0000 1111
2.2 原码、反码、补码
然后再了解一下原码、反码和补码的相关知识,同样只用 8 位做示范
1、原码
原码,即 2.1 所示的转换为二进制,例:15,原码即为 0000 1111。在 2.1 中只用了正数来举例,这里开始需要区分正数和负数,同时引入符号位的概念。二进制的第一位为符号位,正数为 0,负数为 1,符号位不参与位的转换和运算
例:-15,原码即为 1000 1111
15原码: 0000 1111
-15原码:1000 1111
2、反码
反码,即原码按位取反。这里注意,正数的反码与原码相同。例:-15,原码为 1000 1111,符号位不参与转换,按位取反为 1111 0000
15反码: 0000 1111,与原码同
-15原码:1000 1111
-15反码:1111 0000
3、补码
补码,即反码加 1,完整说法应为原码取反加1。同样注意,正数的补码与原码相同。例:-15,反码为 1111 0000,加 1 为 1111 0001
15补码: 0000 1111,与原码同
-15原码:1000 1111
-15反码:1111 0000
-15补码:1111 0001
正数的原码、反码、补码相同,正数的二进制表示为二进制原码即可(其实也是补码,相同不需要计算)。而负数的二进制表示为二进制补码,也就是文章的第一张图片所示示例,如下。由于 int 为 32 位,所以负数显示了一堆 1,正数则是把前面的 0 去掉了

2.3 位运算符
再来了解一下位运算的相关知识,同样只用 8 位来示范
1、<<:按位左移运算符
将转换后的二进制左移指定的位数,例:15 << 2,即 0000 1111 << 2,为 0011 1100,十进制表示为 60。这里后面补的都是 0
0000 1111
0011 1100

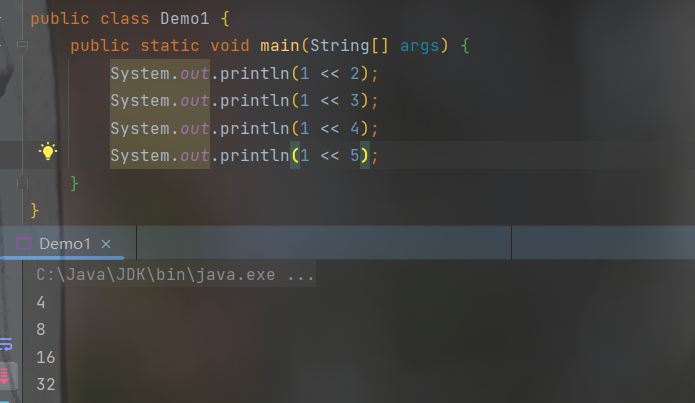
注意:这里可以用 1 << n 来表示 2 的 n 次方,因为其实每左移 1 位,就相当于乘以了一个 2
2、>>:按位右移运算符
将转换后的二进制右移指定的位数,例:15 >> 2,即 0000 1111 >> 2,为 0000 0011,十进制表示为 3。这里前面的补位数是带符号的,正数,符号位为 0,则补 0;负数,符号位为 1,则补 1
0000 1111
0000 0011
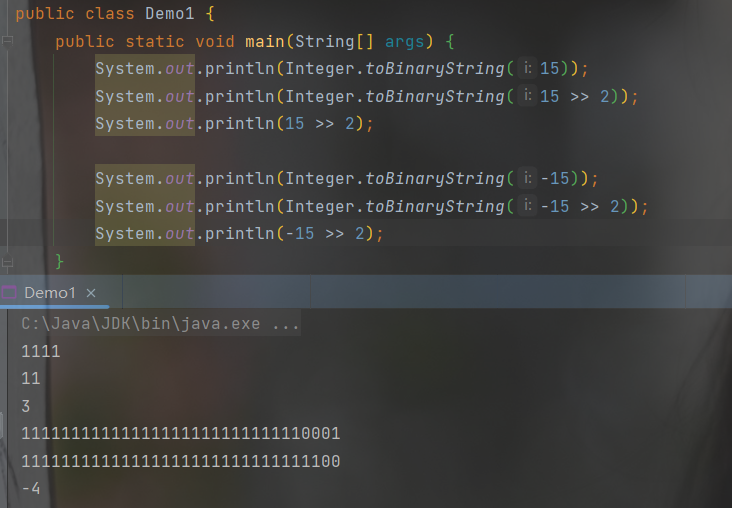
右移可以变相看成是除 2,这时就存在偶数和奇数的情况。偶数,正数和负数的值是相同的,这里说的值指本身的数值,不带符号;奇数时,负数的值比正数大 1
3、>>>:按位右移补零操作符
将转换后的二进制右移指定的位数,移动后的空位以零填充。这里就不区分符号位,因此也叫无符号右移,正数没有影响,因为前面本来就是 0,负数则会改变原本的值大小,例:-15 >>> 2,即 1111 0001 >>> 2,为 0011 1100,这里只用了 8 位来演示,完整 32 位见下图所示,这里前面的 0 被省略了,也可以看到比原来少了两位:
1111 0001
0011 1100
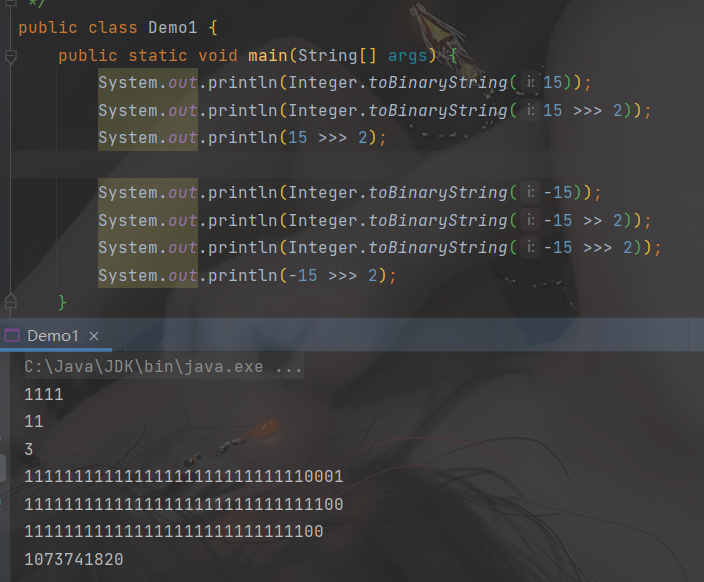
4、&:如果相对应位都是 1,则结果为 1,否则为 0,例:15 & 16、3 & 7
15: 0000 1111 3: 0000 0011
16: 0001 0000 7: 0000 0111
0000 0000 0000 0011
则 15 & 16 结果为 0,3 & 7 结果为 3
2.4 源码解析
1、首先来看调用的顶层方法,这里可以看到就是调用了一个 toUnsignedString0() 的方法,参数 i 即我们传进来需要转换的值,这里的 1,表示的是进制位数,1 即二进制,3 则是 8 进制,4 是 16 进制
public static String toBinaryString(int i) {
return toUnsignedString0(i, 1);
}
public static String toOctalString(int i) {
return toUnsignedString0(i, 3);
}
public static String toHexString(int i) {
return toUnsignedString0(i, 4);
}
2、再来看 toUnsignedString0() 方法,这里先调用了一个 Integer.numberOfLeadingZeros() 方法,这个方法主要用来计算二进制表示的高位连续 0 位的数量,然后用 Integer.SIZE(32) 减去这个数量,计算需要表示的字符数组的长度,可以理解为省略了前面的 0。如下例:
15:0000 0000 0000 0000 0000 0000 0000 1111,原本的表示
15:1111,实际的表示
这一步就可以理解为把前面的 0 省略掉了,只保留需要表示的位数
private static String toUnsignedString0(int val, int shift) {
// assert shift > 0 && shift <=5 : "Illegal shift value";
int mag = Integer.SIZE - Integer.numberOfLeadingZeros(val);
int chars = Math.max(((mag + (shift - 1)) / shift), 1);
char[] buf = new char[chars];
formatUnsignedInt(val, shift, buf, 0, chars);
// Use special constructor which takes over "buf".
return new String(buf, true);
}
@Native public static final int SIZE = 32;
3、接下来来看 Integer.numberOfLeadingZeros() 的具体实现,这里用了一个简易的二分法,分为多个区间 [16, 24, 28, 30] 来进行判断。这里还剩下 [30, 32] 这个区间,为什么没有算呢?见下面的第 6 步。这里的 n 表示高位连续 0 的数量
- 首先判断 i 是否为 0,0 的话则是 32 位的高位连续 0,直接返回 32
- 然后判断 i >>> 16 是否为 0,可以理解为先二分判断一半的区间,假如为 0,则表示至少包含 16 个高位连续 0,n 加上 16,然后 i <<= 16,将 i 去除 16 位 0 再进行后续判断
- 判断 i >>> 24 是否为 0,即判断是否至少包含 8 个高位连续 0,假如为 0,则 n 加上 8,然后 i <<= 8,将 i 去除 8 位 0 再进行后续判断
- 同上,判断是否至少包含 4 个高位连续 0
- 同上,判断是否至少包含 2 个高位连续 0,这里已经为 i >>> 30
- 最后,这里还剩下了 [30, 32] 这个长度为 2 的区间,存在四种情况,[00, 01, 10, 11],在最前面我们已经判断了等于 0 的情况,所以 00 是排除掉的,剩下 [01, 10, 11],假如是 x1,那么就不需要判断 x 是多少了,因为只需要判断最高连续 0 位;假如是 x0,由于 00 已经排除,则 x 为 1。所以,其实只需要判断一位就足够了,这也是为什么没有算 [30, 32] 这个区间,只到了 31 为止
这里先给 n 赋了初始值为 1,先假设默认这一位是 0,然后再通过n -= i >>> 31,判断这一位到底是什么,是 0 则 n = n - 0,不变;是 1 则 n = n - 1,减掉原先赋的默认初始值 1。这里其实就是用这个技巧代替了if (i >>> 31 == 0) { n += 1; }的判断,如下第二种写法
public static int numberOfLeadingZeros(int i) {
// HD, Figure 5-6
if (i == 0)
return 32;
int n = 1;
if (i >>> 16 == 0) { n += 16; i <<= 16; }
if (i >>> 24 == 0) { n += 8; i <<= 8; }
if (i >>> 28 == 0) { n += 4; i <<= 4; }
if (i >>> 30 == 0) { n += 2; i <<= 2; }
n -= i >>> 31;
return n;
}
public static int numberOfLeadingZeros(int i) {
// HD, Figure 5-6
if (i == 0)
return 32;
int n = 0;
if (i >>> 16 == 0) { n += 16; i <<= 16; }
if (i >>> 24 == 0) { n += 8; i <<= 8; }
if (i >>> 28 == 0) { n += 4; i <<= 4; }
if (i >>> 30 == 0) { n += 2; i <<= 2; }
if (i >>> 31 == 0) { n += 1; }
return n;
}
4、再回到 toUnsignedString0() 这个方法,通过调用 numberOfLeadingZeros() 得到高位连续 0 的数量,然后通过 Integer.SIZE 减去这个数量得到需要表示的位数
然后再通过 Math.max(((mag + (shift - 1)) / shift), 1); 来计算 2/8/16 进制对应的字符数组的长度,这里的参数 shift 前面提到是用来表示进制位数,1 即二进制,3 则是 8 进制,4 是 16 进制
得到字符数组长度后创建对应的字符数组,调用 formatUnsignedInt() 来填充数组
private static String toUnsignedString0(int val, int shift) {
// assert shift > 0 && shift <=5 : "Illegal shift value";
int mag = Integer.SIZE - Integer.numberOfLeadingZeros(val);
int chars = Math.max(((mag + (shift - 1)) / shift), 1);
char[] buf = new char[chars];
formatUnsignedInt(val, shift, buf, 0, chars);
// Use special constructor which takes over "buf".
return new String(buf, true);
}
5、formatUnsignedInt() 方法如下,参数 val 是需要转换的值;shift 表示进制位数,这里为 1;buf 为创建的字符数组;offset 为偏移量,这里为 0;len 为数组长度。其中第 6 行用到的 Integer.digits 是定义好的包含全部数字和字母的字符数组
这里其实就是按照对应的位数进行对应填充
-
将数组长度赋值给 charPos,后续用 charPos 来进行计算
-
radix = 1 << shift,前面说过,1 << n 其实就是 2 的 n 次方,这里是用来表示进制,二进制则是 2 的 1 次方,八进制是 2 的 3 次方,十六进制是 2 的 4 次方 -
mask 为进制减一,用来后续和 val 做 & 运算,实际就是逐批匹配进制对应的位数。例:shift 为 3,即 8 进制,mask 则为 7
8 == radix = 1 << 3;
7 == mask = radix - 1;mask 做 & 运算时,表示为 111,即 3 位二进制表示一位 8 进制
-
val & mask 得到值后,在 digits 数组里去找到对应的索引的字符赋给 buf,即创建的字符数组,注意,这里是倒序存放,对应进制位数的变化,从右往左
-
然后将 val 右移相应的进制位数,循环匹配
-
最后返回填充好的字符数组
static int formatUnsignedInt(int val, int shift, char[] buf, int offset, int len) {
int charPos = len;
int radix = 1 << shift;
int mask = radix - 1;
do {
buf[offset + --charPos] = Integer.digits[val & mask];
val >>>= shift;
} while (val != 0 && charPos > 0);
return charPos;
}
final static char[] digits = {
'0' , '1' , '2' , '3' , '4' , '5' ,
'6' , '7' , '8' , '9' , 'a' , 'b' ,
'c' , 'd' , 'e' , 'f' , 'g' , 'h' ,
'i' , 'j' , 'k' , 'l' , 'm' , 'n' ,
'o' , 'p' , 'q' , 'r' , 's' , 't' ,
'u' , 'v' , 'w' , 'x' , 'y' , 'z'
};
6、再回到 toUnsignedString0() 方法,最后一步则是将字符数组转换为 String 返回,到这里整个流程结束
private static String toUnsignedString0(int val, int shift) {
// assert shift > 0 && shift <=5 : "Illegal shift value";
int mag = Integer.SIZE - Integer.numberOfLeadingZeros(val);
int chars = Math.max(((mag + (shift - 1)) / shift), 1);
char[] buf = new char[chars];
formatUnsignedInt(val, shift, buf, 0, chars);
// Use special constructor which takes over "buf".
return new String(buf, true);
}