1.自我介绍

基数排序(radix sort)属于“分配式排序” (distribution sort)，又称“桶子法” (bucket sort)或bin sort,它是通过键值的各个位的值,将要排序的元素分配至某些“桶”中,是‘桶排序’的扩展

2.基本思想

将所有待比较数值统一为同样的数位长度,数位较短的数前面补零。然后,从最低位开始,依次进行一次排序。这样从最低位排序一直到最高位排序完成以后，数列就变成一个有序序列。

 3.代码山

 public static void radixSort(int[] array) {

        //1.定义二维数组，表示十个桶
        //2.二维数组包含十个一维数组，防止溢出定义为array.length
        //3.空间换时间
        int[][] bucket = new int[10][array.length];

        //记录每个桶，实际存放多少个数据，定义一个一维数组
        //bucketCounts[0],就是记录bucket[0]桶的放入数据的个数
        int[] bucketCounts = new int[10];

        //得到数组中，最大数的位数
        int max = array[0];//假设数组中，第一个数最大
        for (int i = 1; i < array.length; i++) {
            if (array[i] > max) {
                max = array[i];
            }
        }
        //得到最大数的位数
        int maxLength = (max + "").length();

        for (int i = 0, n = 1; i < maxLength; i++, n *= 10) {
            //第一轮排序（每个元素的个位）
            for (int j = 0; j < array.length; j++) {
                int geWei = array[j] / n % 10;
                bucket[geWei][bucketCounts[geWei]] = array[j];
                bucketCounts[geWei]++;
            }

            //按照这个桶的顺序取
            //遍历每一个桶，把数据放回原数组
            int index = 0;
            for (int k = 0; k < bucketCounts.length; k++) {
                //如果桶中有数据，放回原数组，否则直接pass
                if (bucketCounts[k] != 0) {
                    //循环第k个桶
                    for (int l = 0; l < bucketCounts[k]; l++) {
                        //取出元素放入array中
                        array[index] = bucket[k][l];
                        index++;
                    }
                }
                //第i+1轮后，每个桶置为0
                bucketCounts[k] = 0;
            }
            System.out.println("第"+(i+1)+"轮后:array="+Arrays.toString(array));
        }

    }

4.测试 

        int[] array = new int[]{2,3,4,5,15,19,26,27,36,38,44,46,47,48,50};
        radixSort(array);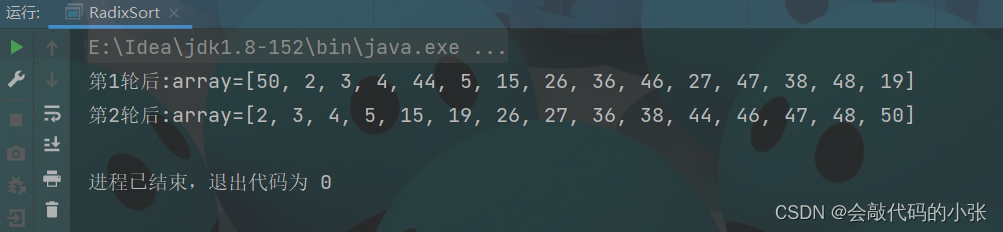

5.总结 

加入负数可以发现，程序直接报错

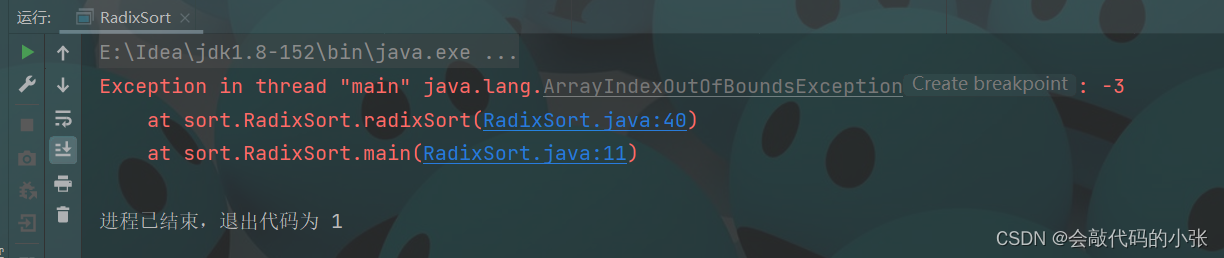
原因：桶的下表是从0开始的，加入负数，会越界 

如果有负数加入排序，就不推荐用基数排序了~~