考试章节范围


第一章:1.1、1.2、1.3
填空
- 顶点集和边集都有限的图,称为有限图
- 只有一个顶点的图,称为平凡图
- 边集为空的图,称为空图
- 顶点数为n的图,称为n阶图
- 连接两个相同顶点的边的条数称为边的重数;重数大于1的边,称为重边
- 端点重合为一点的边,称为环
- 既无环又无重边的图,称为简单图
- 每两个不同的顶点之间都有一条边相连的简单图称为完全图 ,记为
K
n
K_n
Kn,
n
n
n为顶点数目

- 任何图中,奇次顶点的总数必为偶数
- 图同构的必要条件: (1) 顶点数相同(2) 边数相同(3) 关联边数相同的顶点个数相同。
- 4个顶点可以组成11个简单图
- K 4 K_4 K4分为4个平面
- 如果图G的一个子图包含G的所有顶点,称该子图为G的一个生成子图
- 图G= (V, E)中所有顶点的度的和等于边数m的2倍(握手定理)
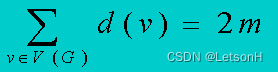
- 奇数度的顶点称为奇点,偶数度的顶点称偶点。
作业





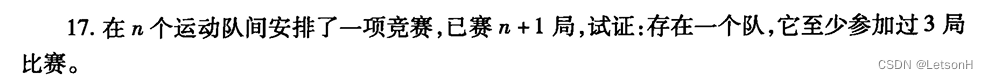

第二章:2.1、2.4、2.5
填空
- 边不重复但顶点可重复的通路,称为道路
- 顶点不重复的通路,称为路径
- G中任意两点都连通,称为G连通
- 起点和重点重合的路径,称为圈
- 一条路径所含边的数目,称为这条路径的长度
- 一个图是偶图(二部图)当且当它不包含奇圈
- 不含圈的图称为无圈图,树是连通的无圈图
- 每棵非平凡树至少有两片树叶。
- 图G是树当且仅当G中任意两点都被唯一的路连接。
- 每个n阶连通图的边数至少为n-1
- 任意树T的两个不邻接顶点之间添加一条边后,可以得到唯一圈。
- 每个连通图至少包含一棵生成树。
计算
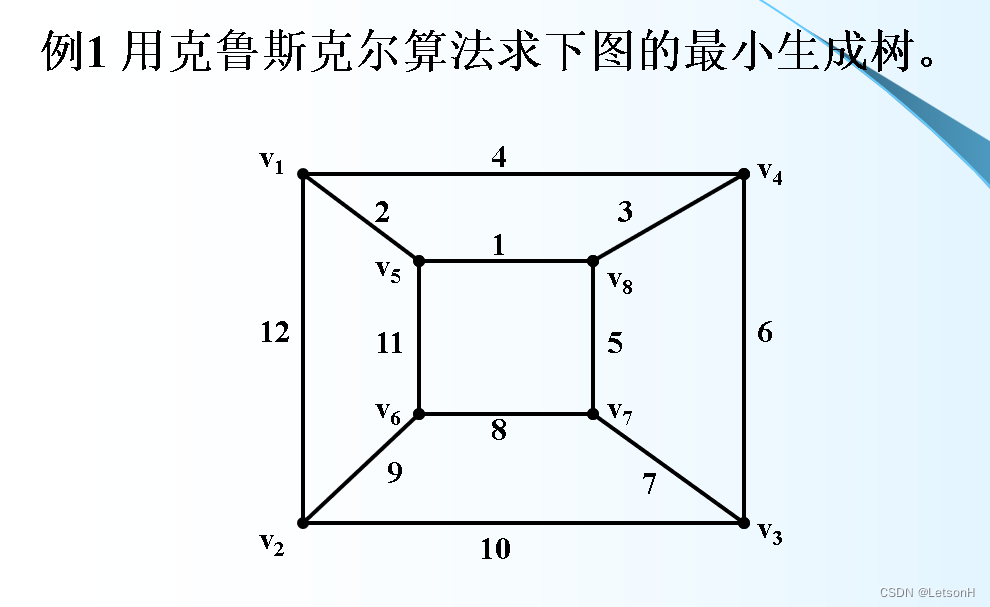

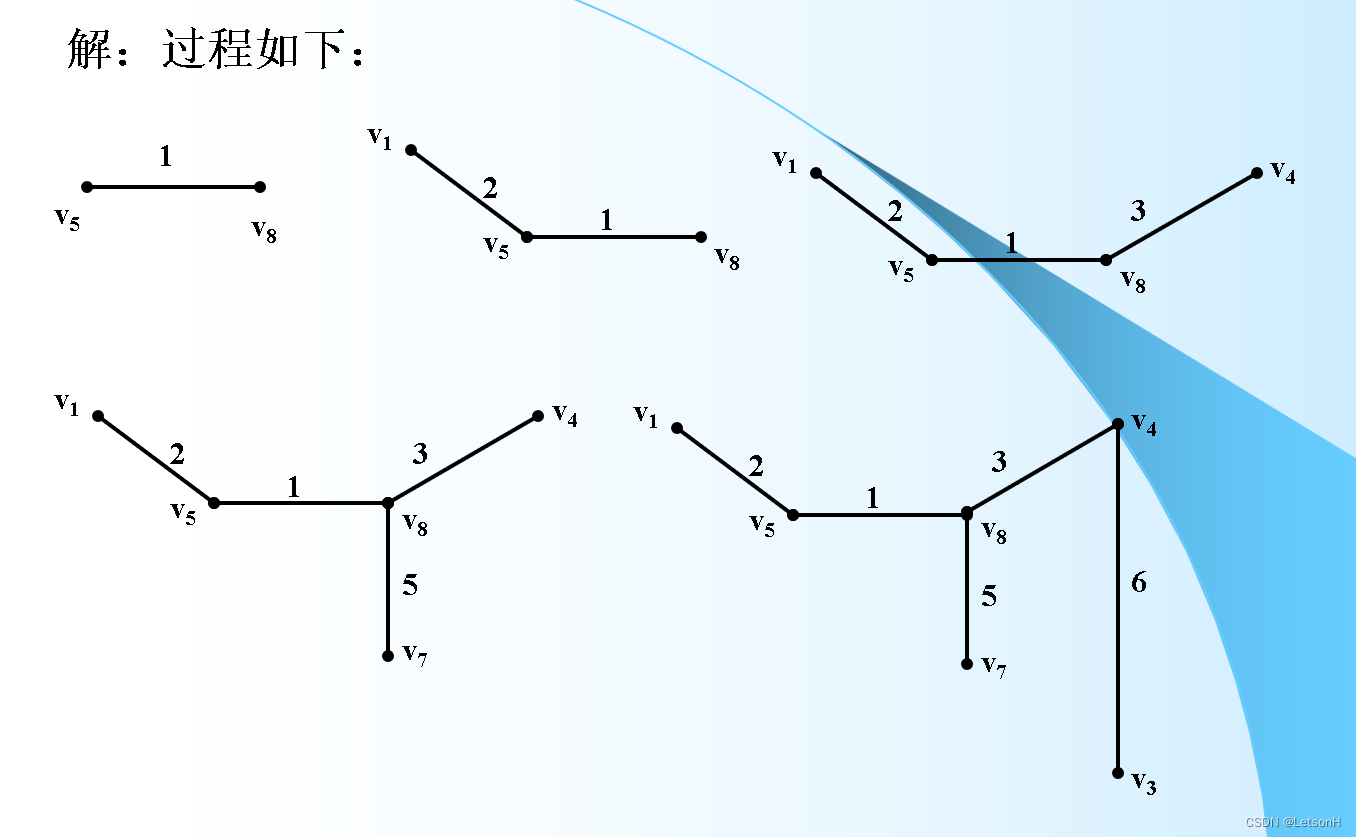
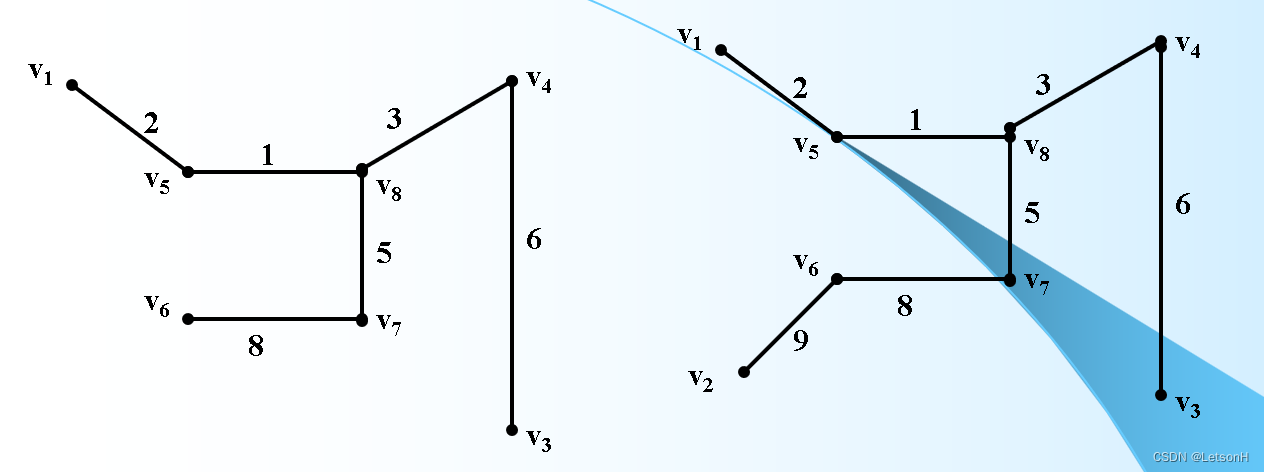
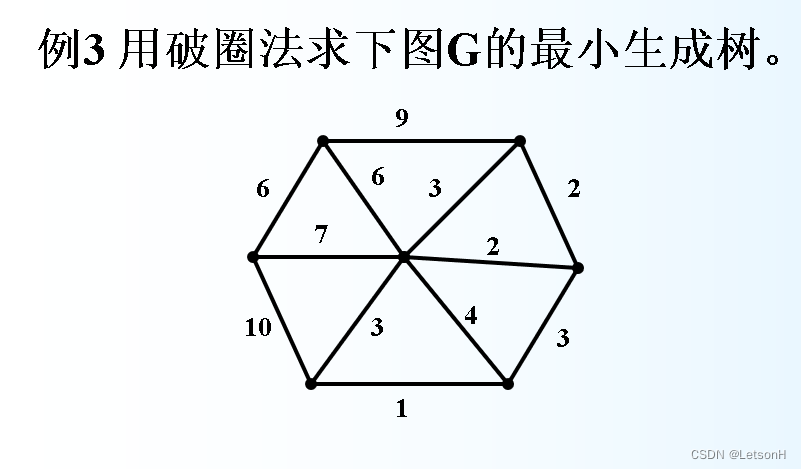

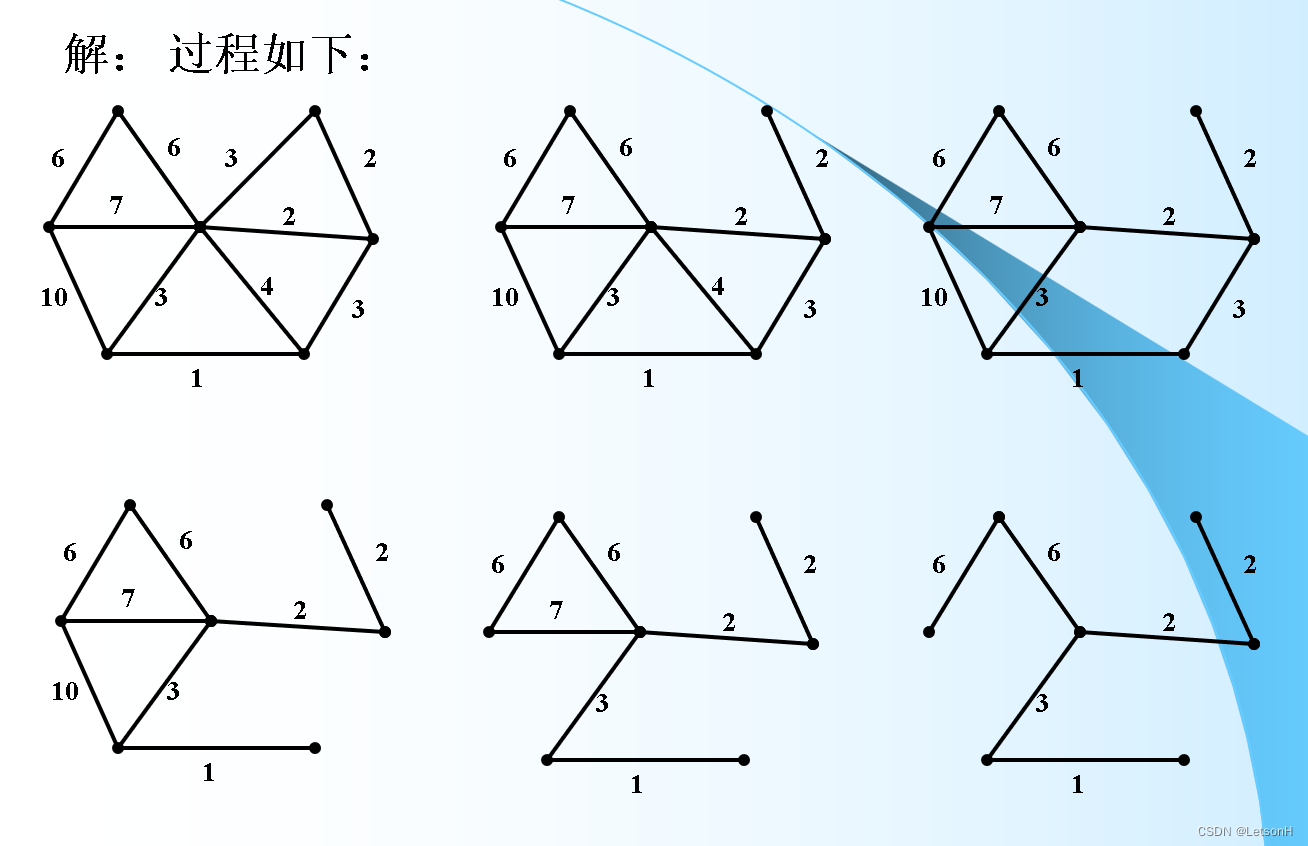
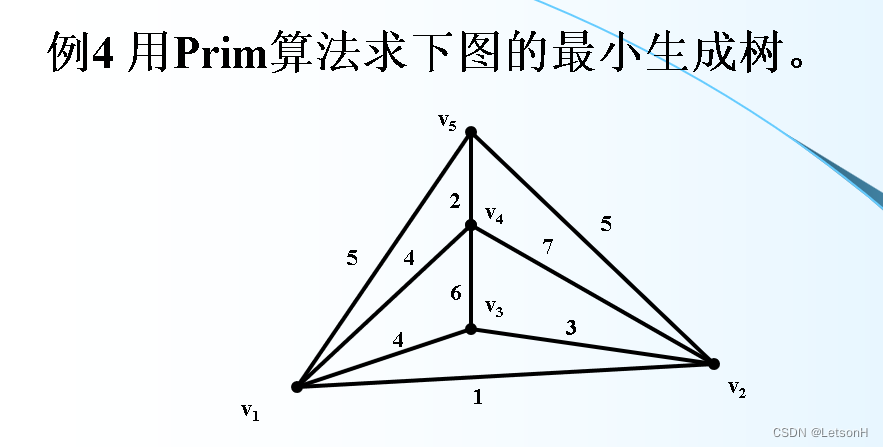

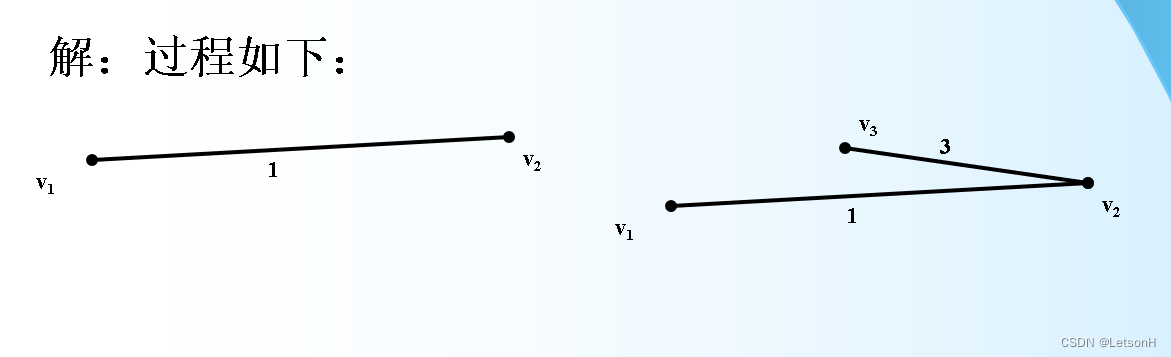
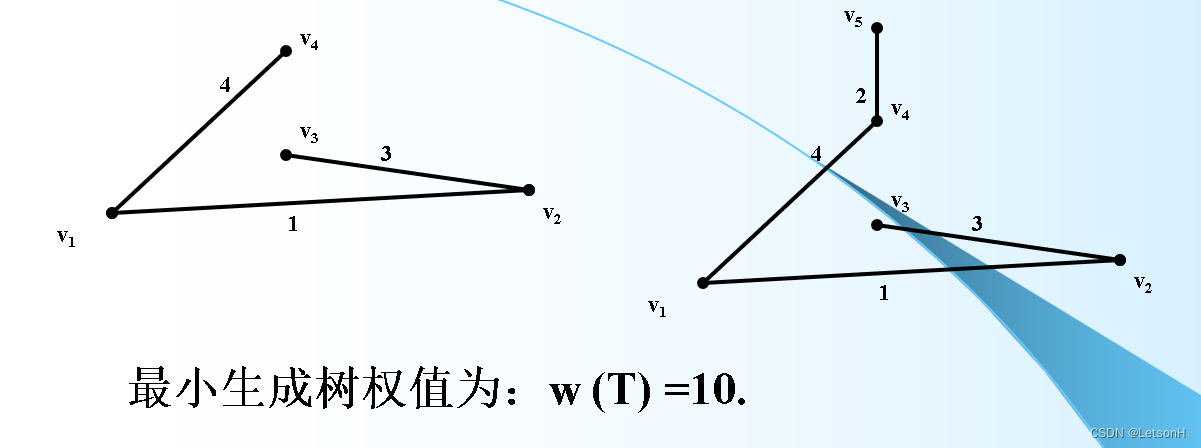
作业


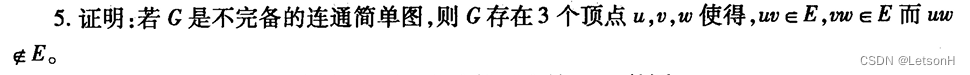


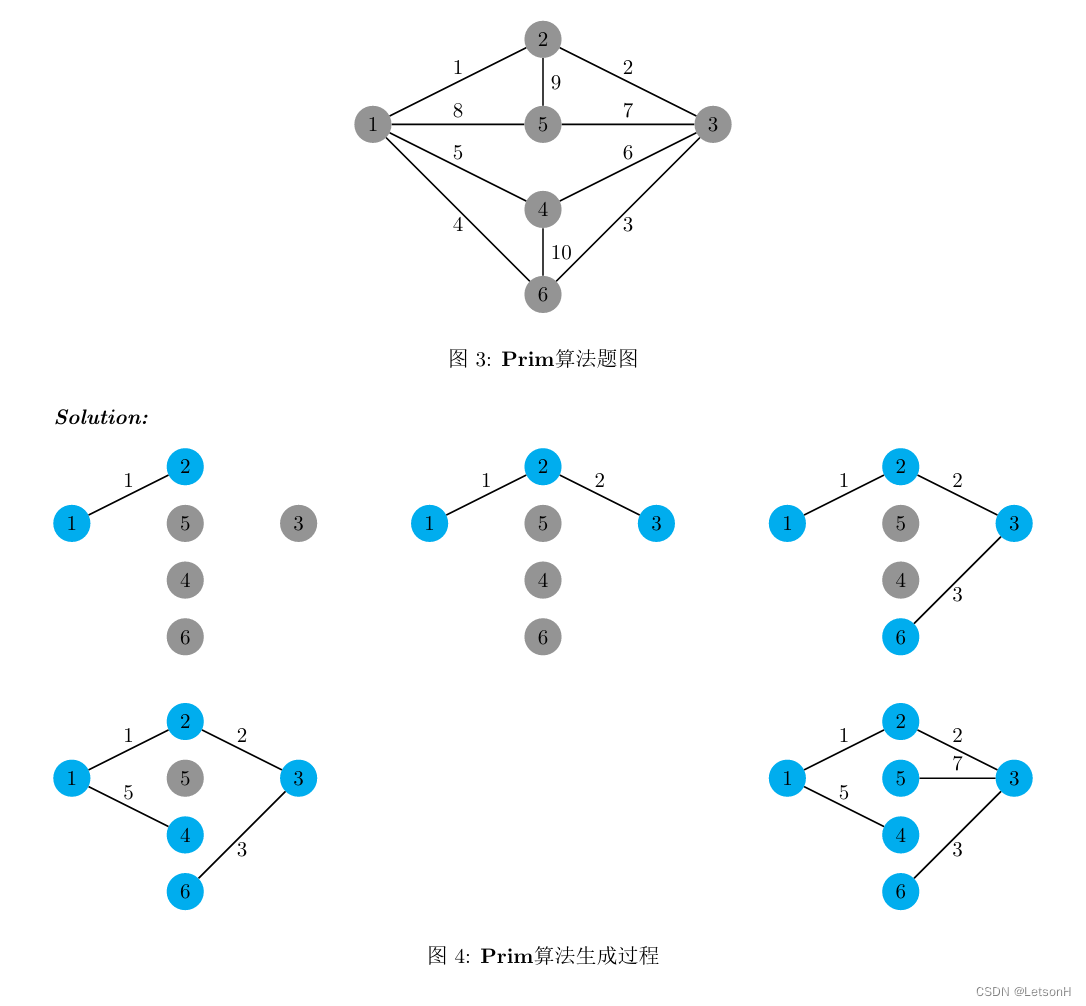
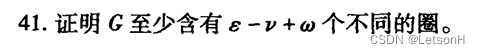

第三章:3.1、3.2
填空
- 设e是图G的一条边,若ω(G-e)>ω(G), 则称e为G的割边。
- e是图G的割边当且仅当e不在G的任何圈中。
- 设 v 是树的顶点,则 v是G 的割点当且仅当 d(v)>=2
作业

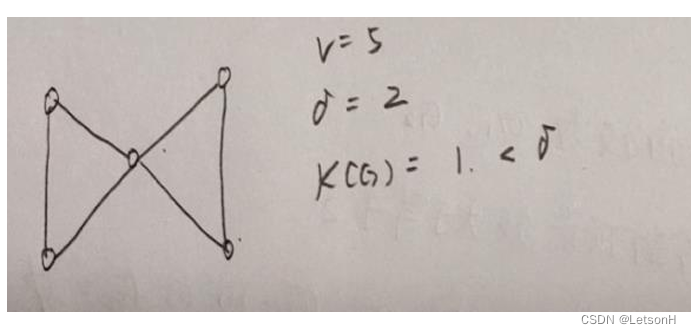


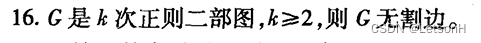



第四章:4.1
计算
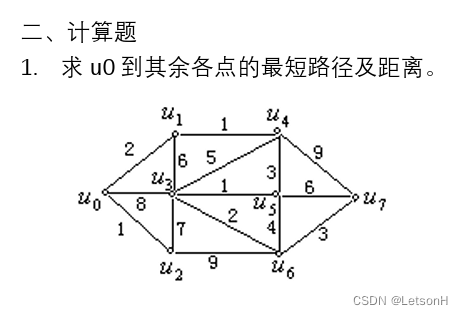
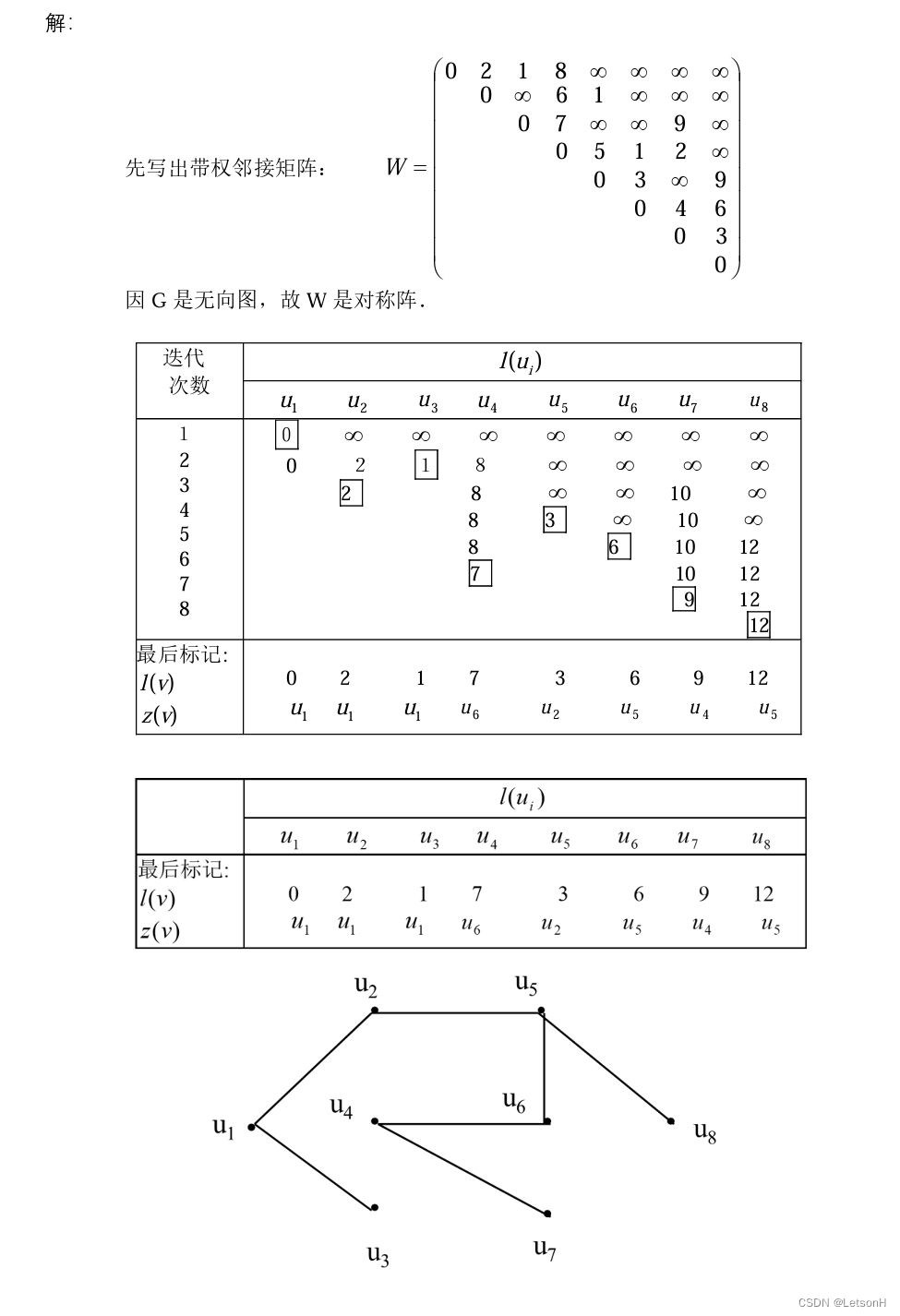
Floyd算法:求任意两点间的最短路.
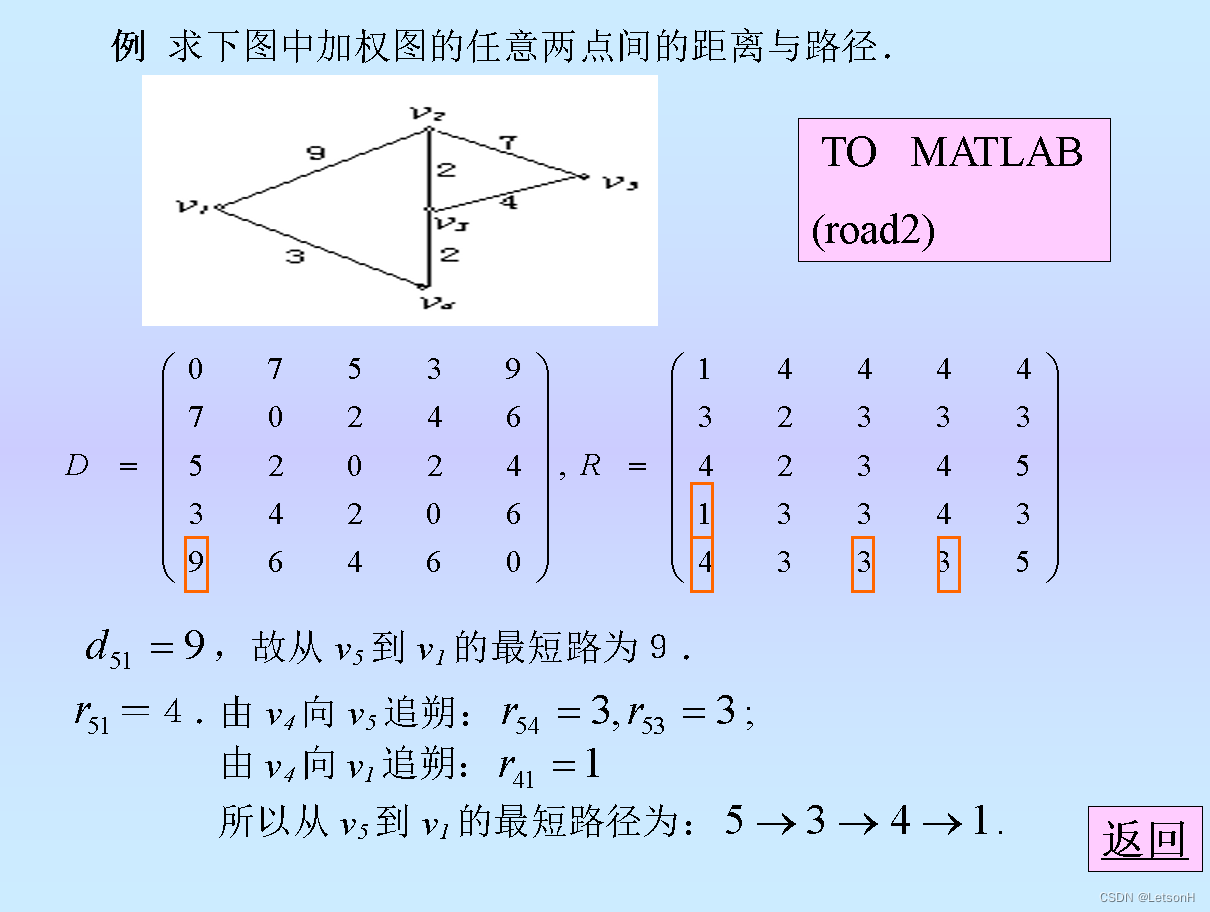
作业
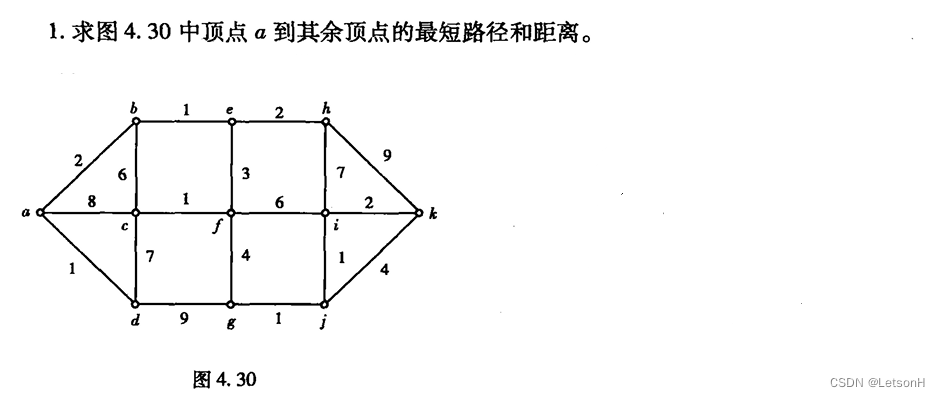
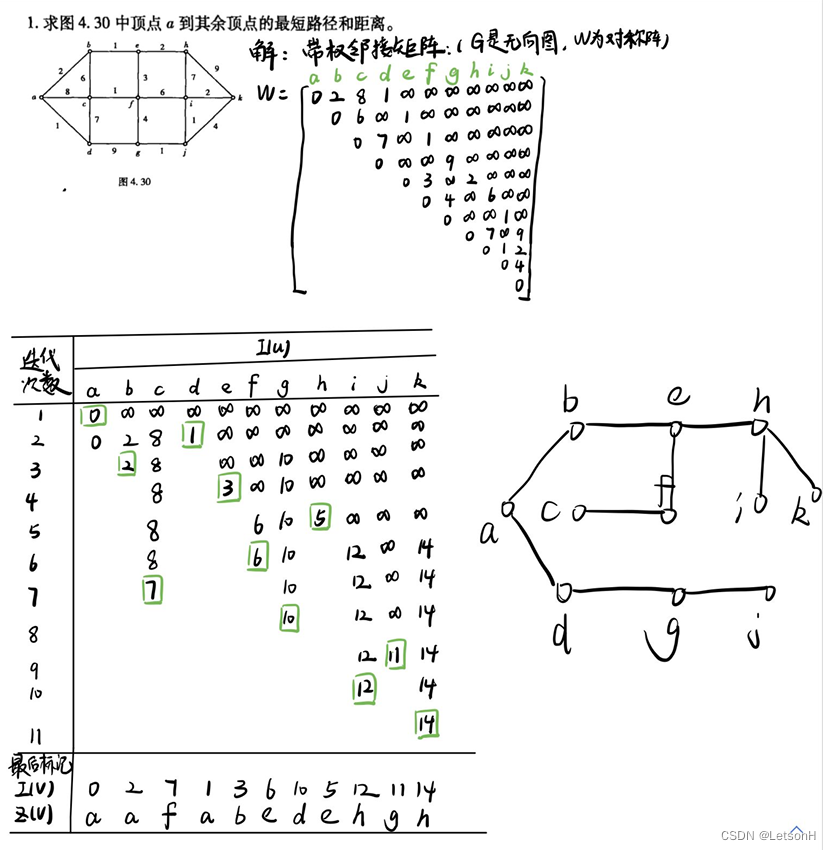


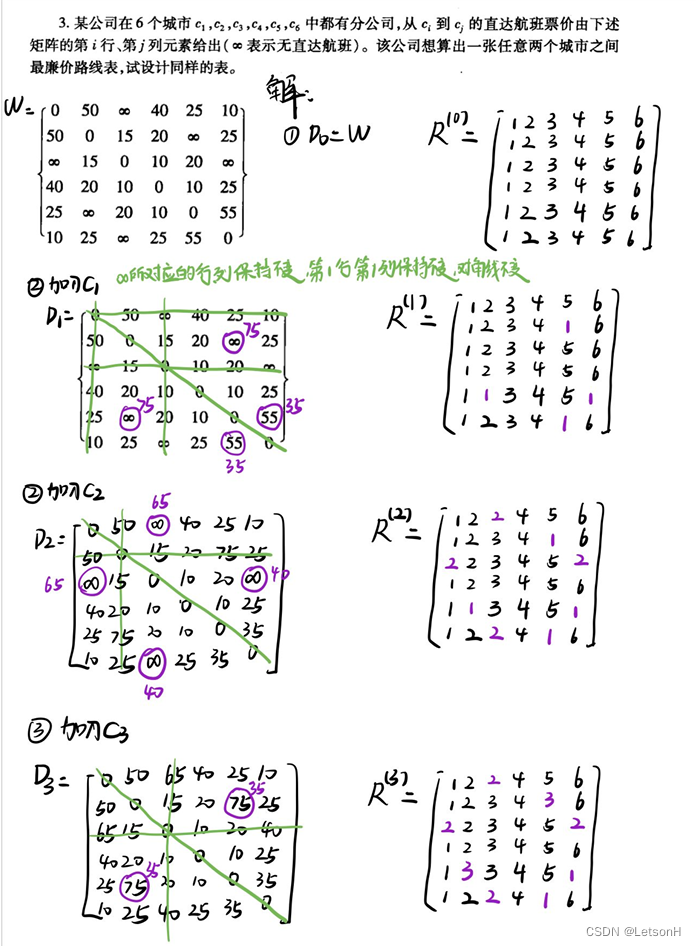
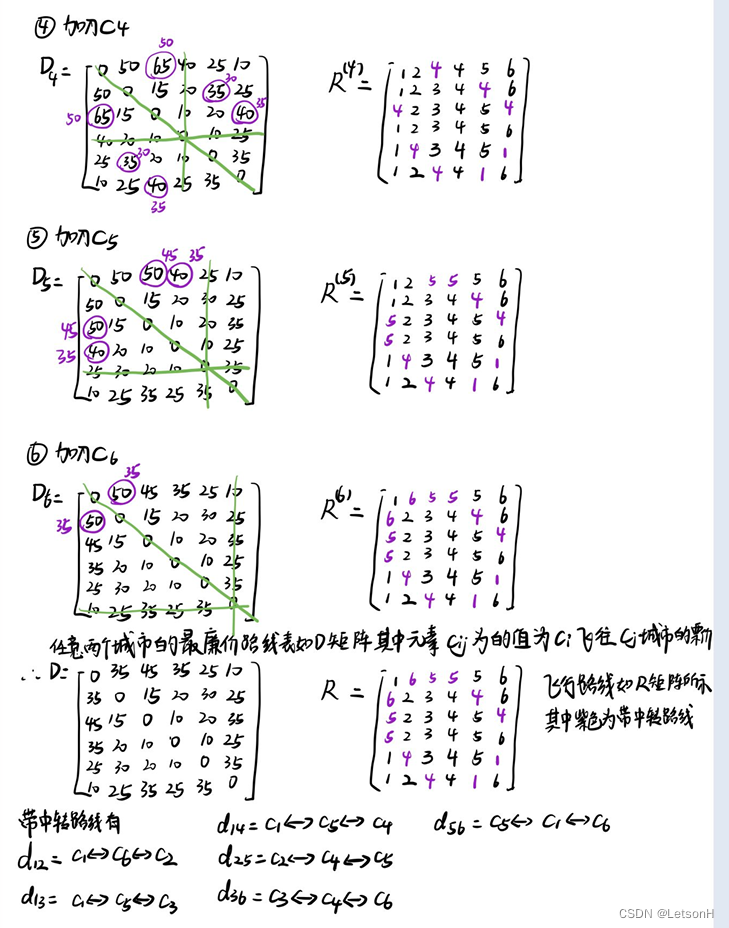
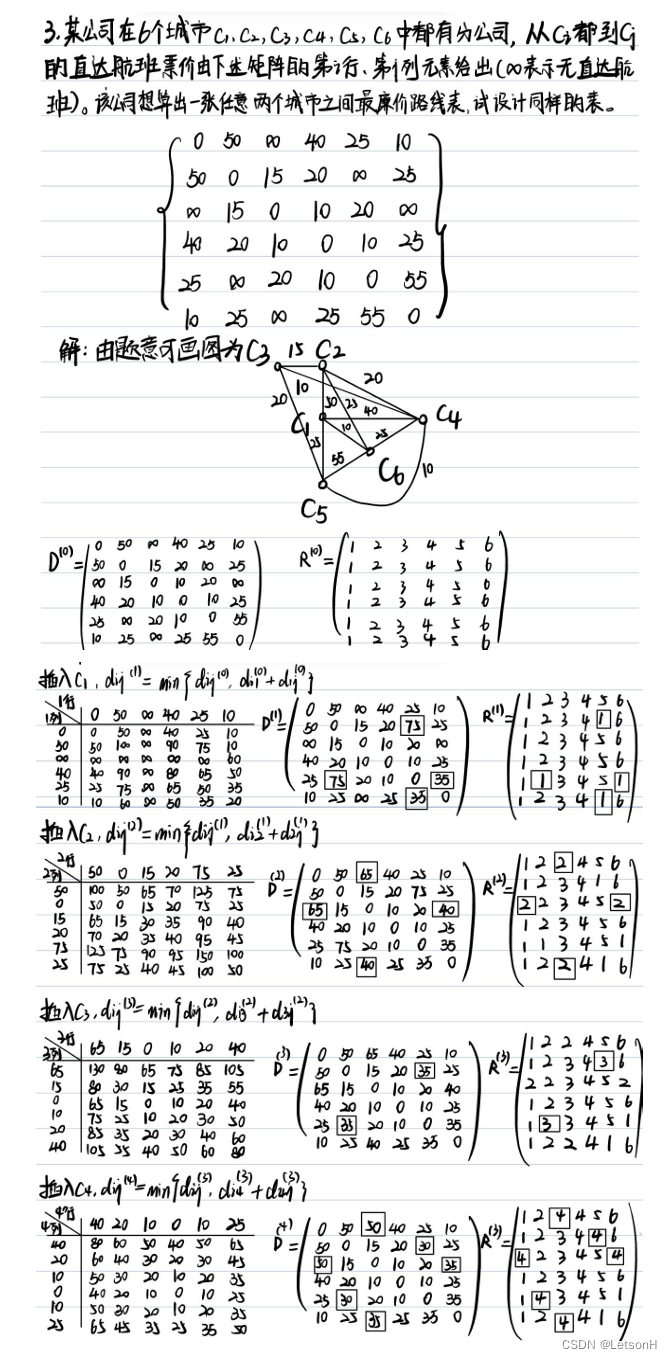

第五章:5.1、5.2、5.3、5.4
填空
- 匹配 M— 如果M是图G的边子集(不含环),且M中的任意两条边没有共同顶点,则称M是G的一个匹配。
- 最大匹配 M— 如果M是图G的包含边数最多的匹配,称M是G的一个最大匹配。特别是,若最大匹配饱和了G的所有顶点,称它为G的一个完美匹配(理想匹配)。
- M交错路— 如果M是图G的匹配,G中一条由M中的边和非M中的边交错形成的路,称为G中的一条M交错路。特别地,若M交错路的起点与终点是M非饱和点,称这种M交错路为M可扩路(可增长路径)
- (贝尔热,1957) G的匹配M是最大匹配,当且仅当G不包含M可扩路
- 设M是G的匹配,K是G的覆盖,若|M|=|K|,则M是最大匹配,而K是最小覆盖。
- (哥尼,1931) 在偶图中,最大匹配的边数等于最小覆盖的顶点数
- (托特定理,1947) 图G有完美匹配当且仅当对V的任意非空真子集S, 有:
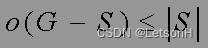
计算
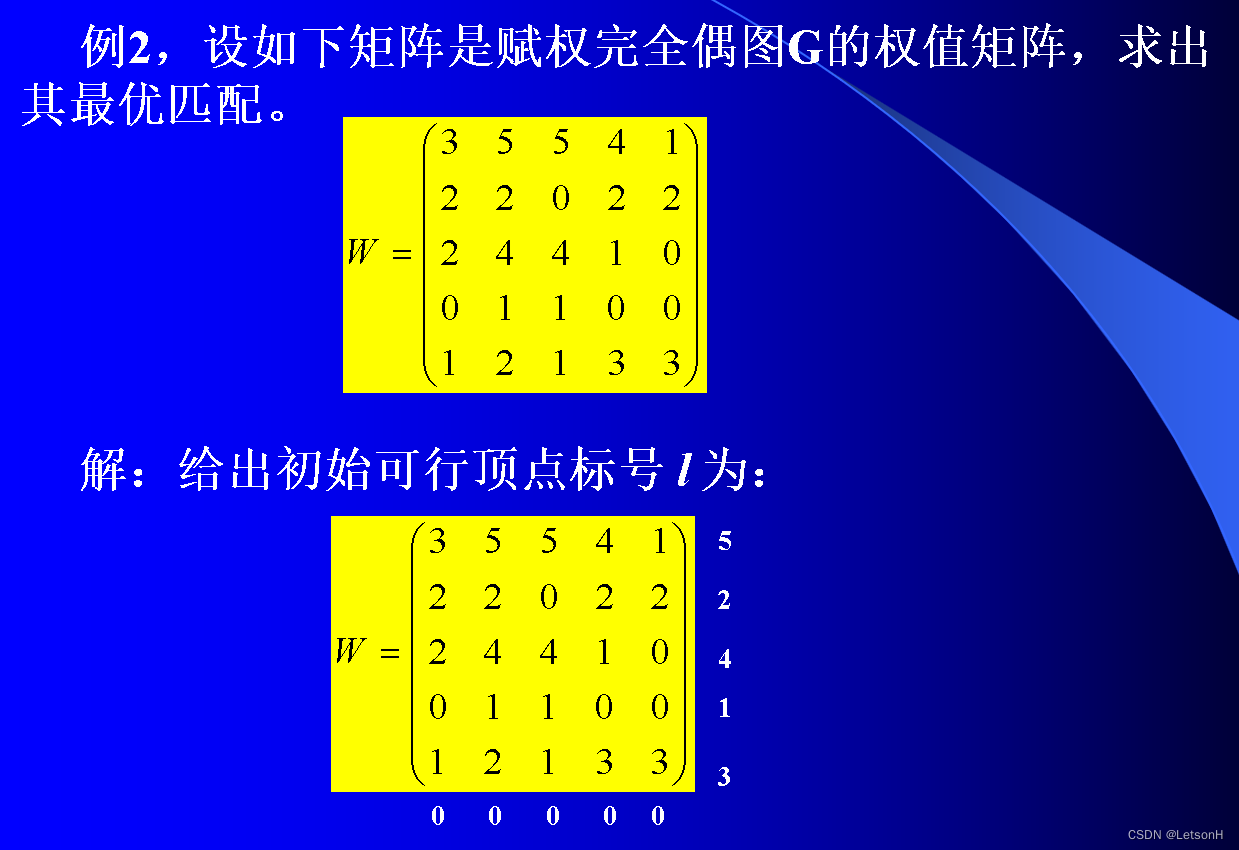
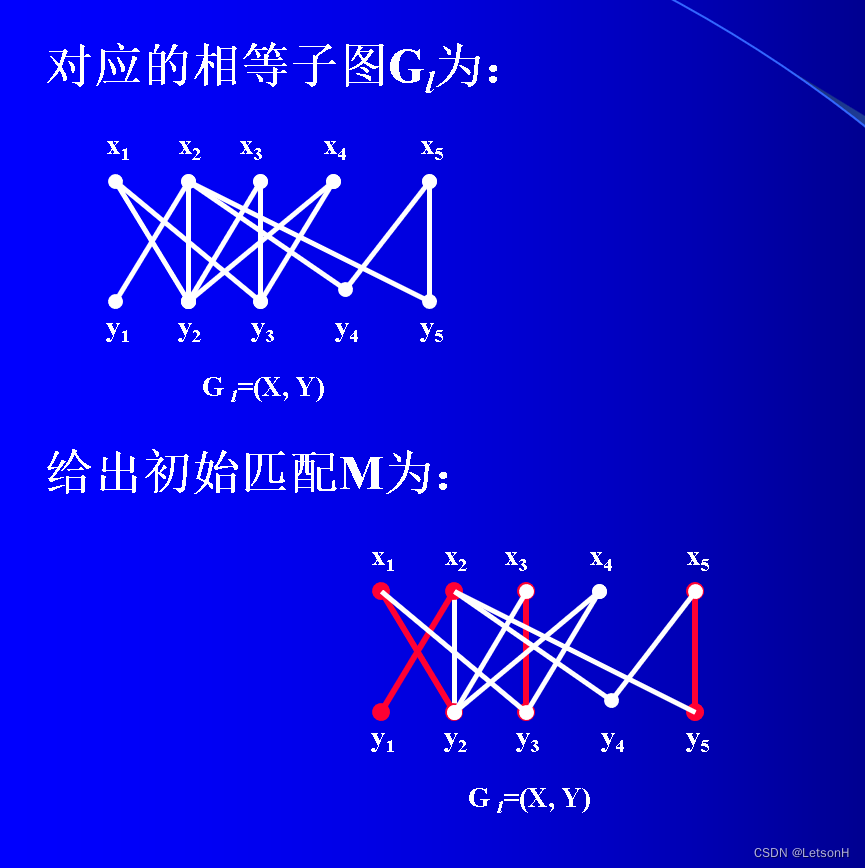

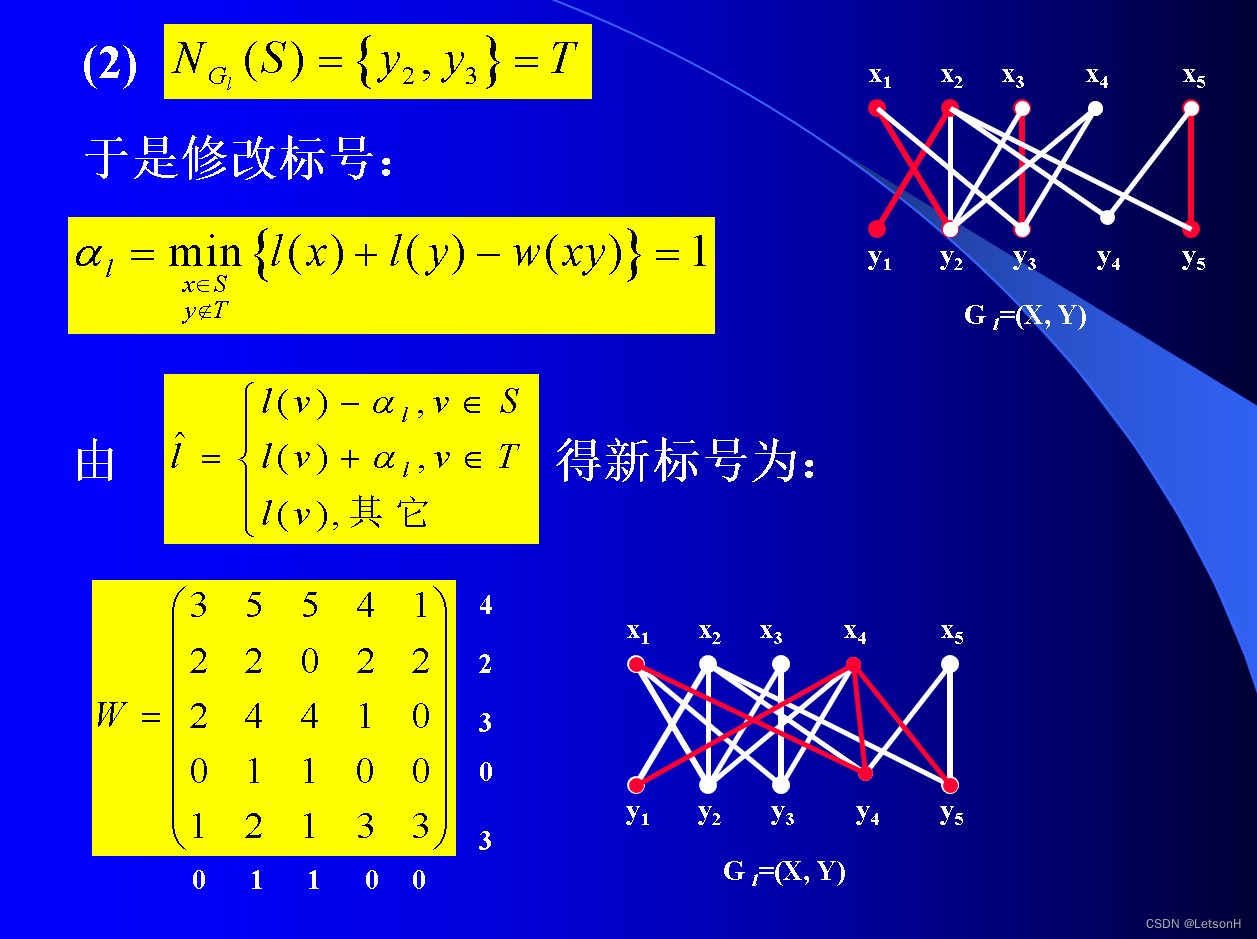

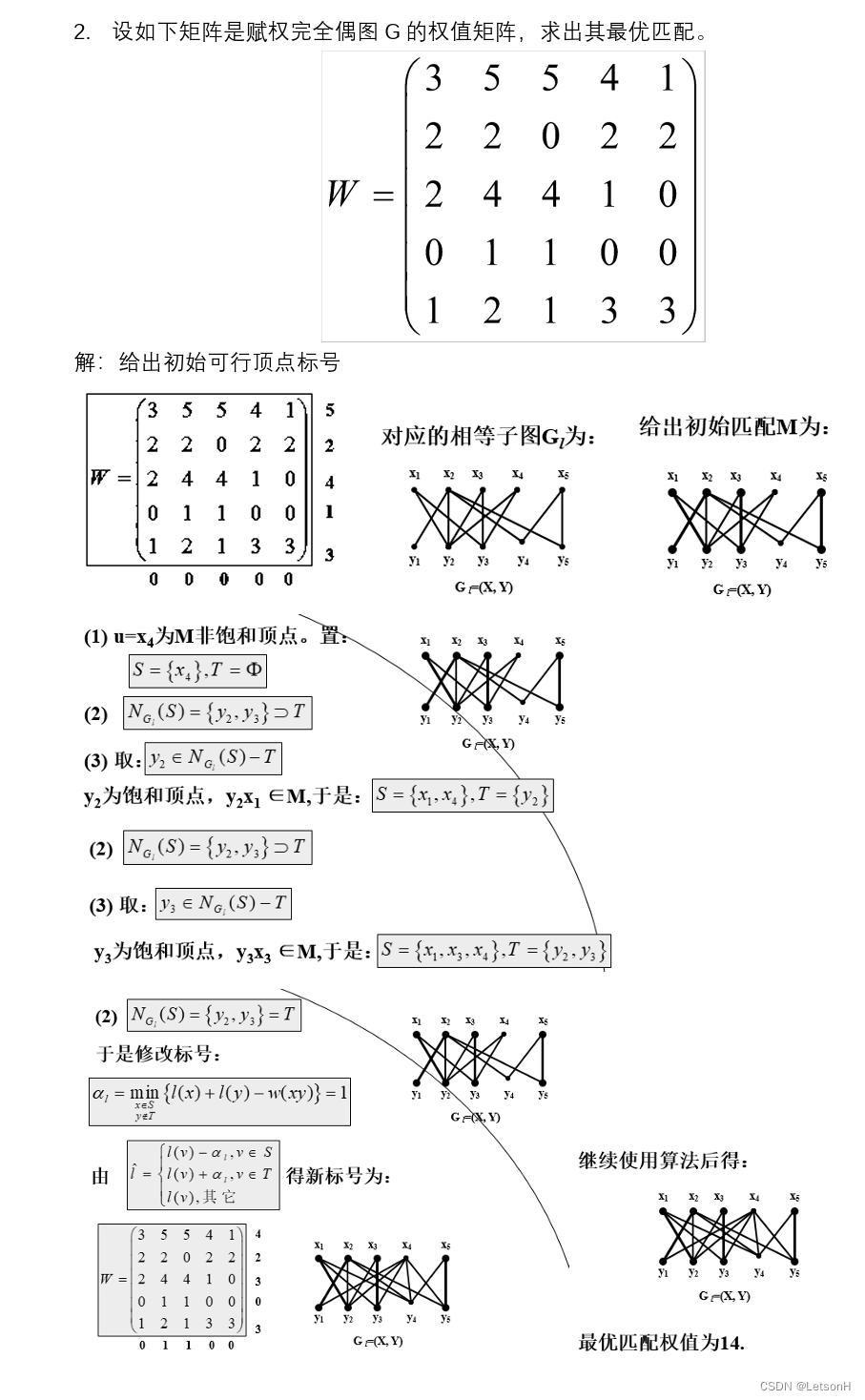

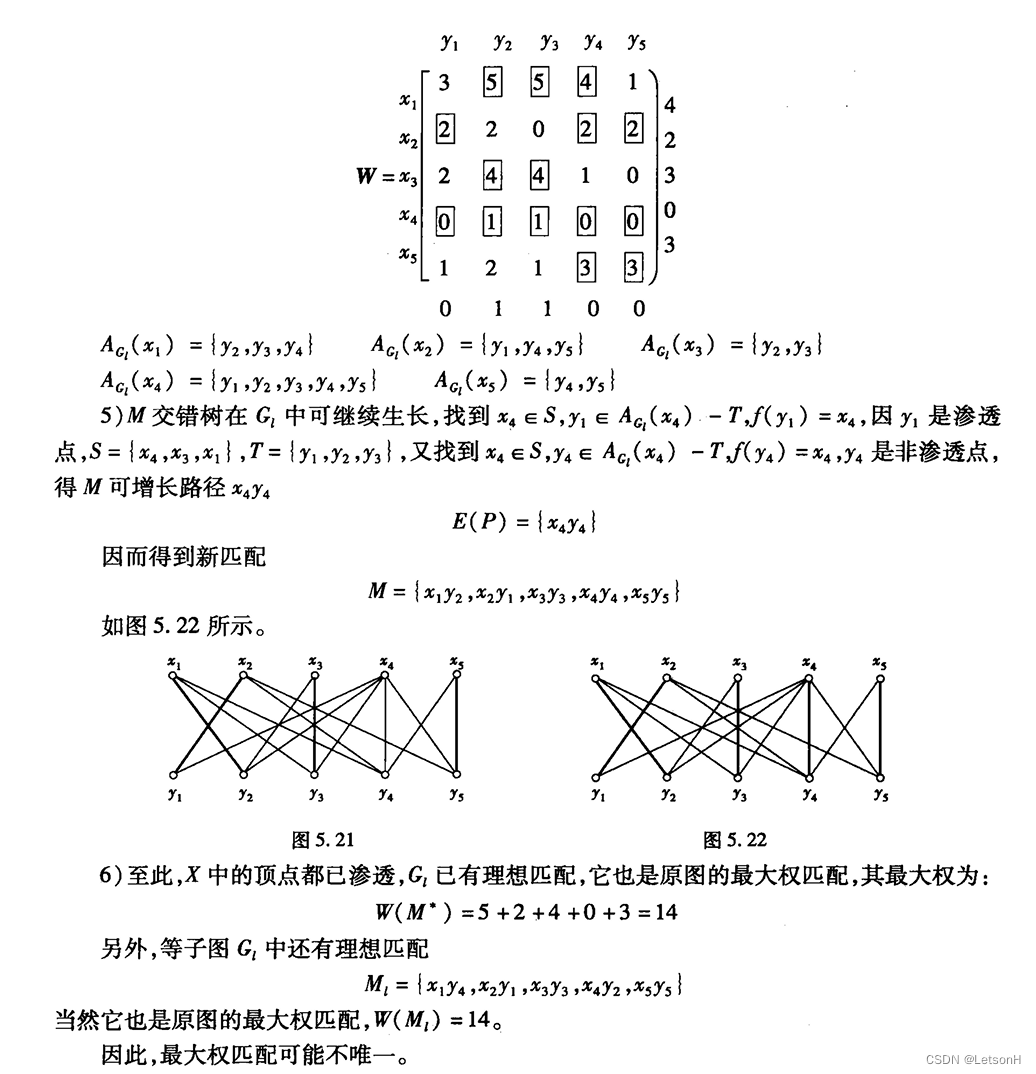
作业
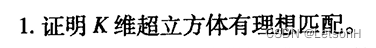



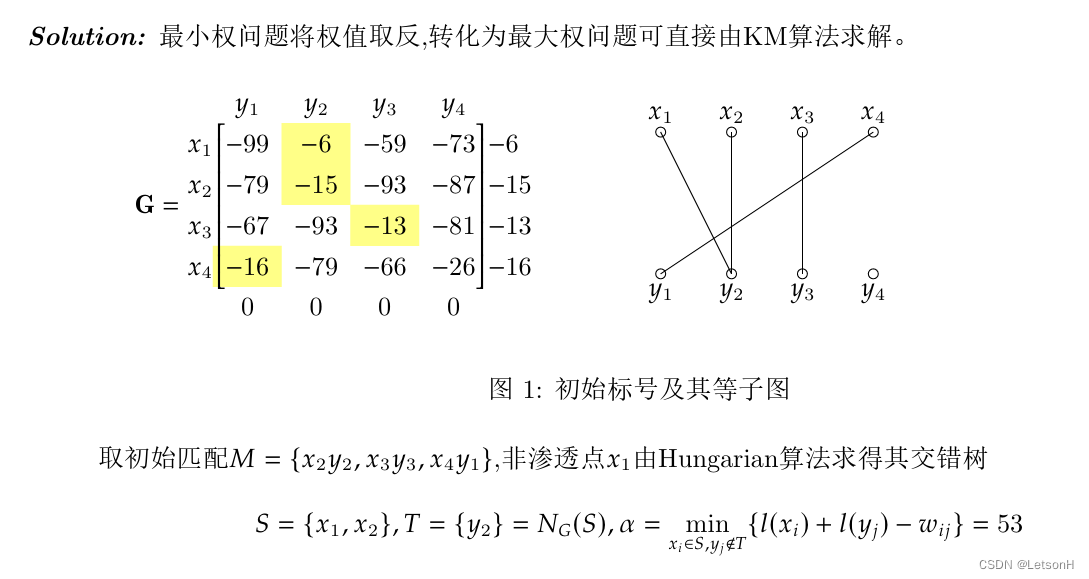

第六章:6.1、6.2、6.5、6.8、6.9
(TSP两边、迭代)
填空
-
设G是H图的充分条件(充分条件) 对于n≧3的简单图G,如果G中有:
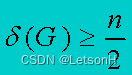
-
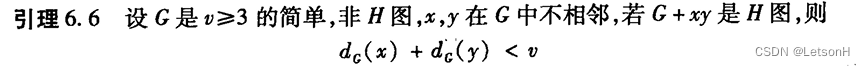
-

-
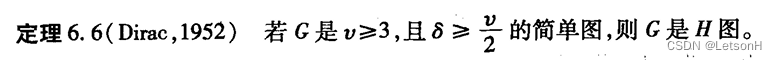
-
设 G 是非平凡连通图。G 有欧拉道路的充要条件是 G 多只有两个次顶点。
-
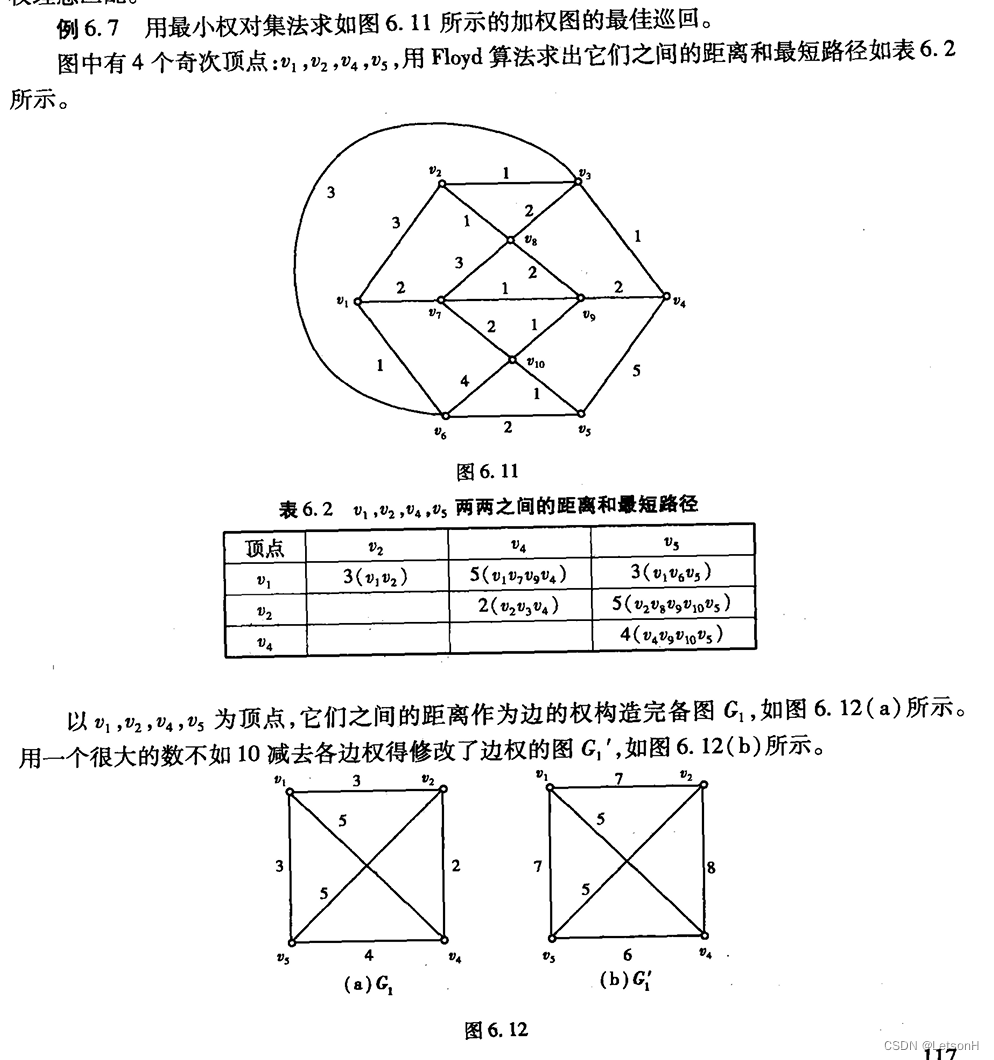
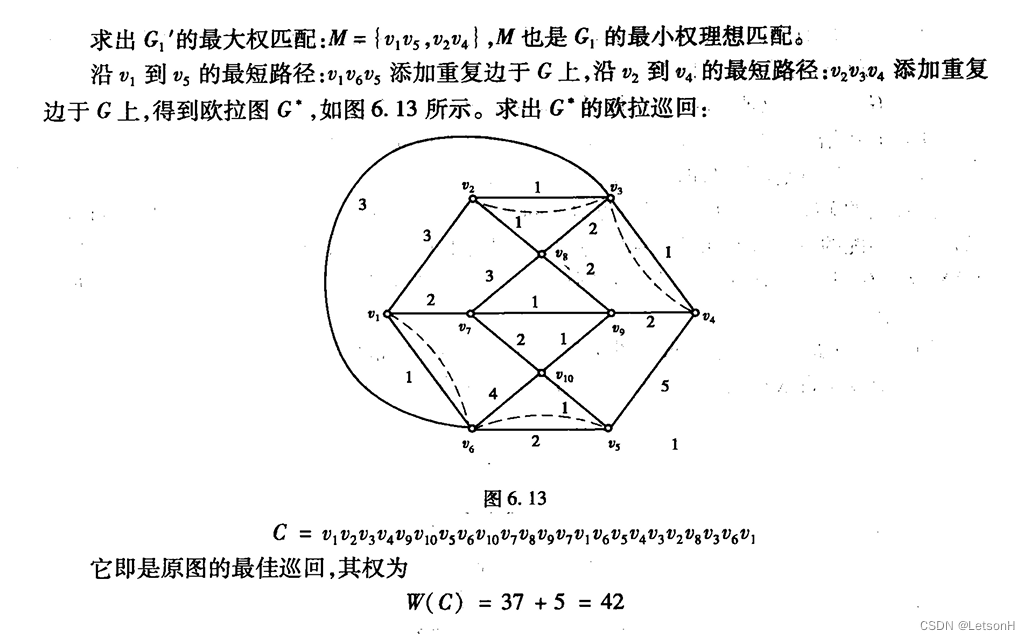
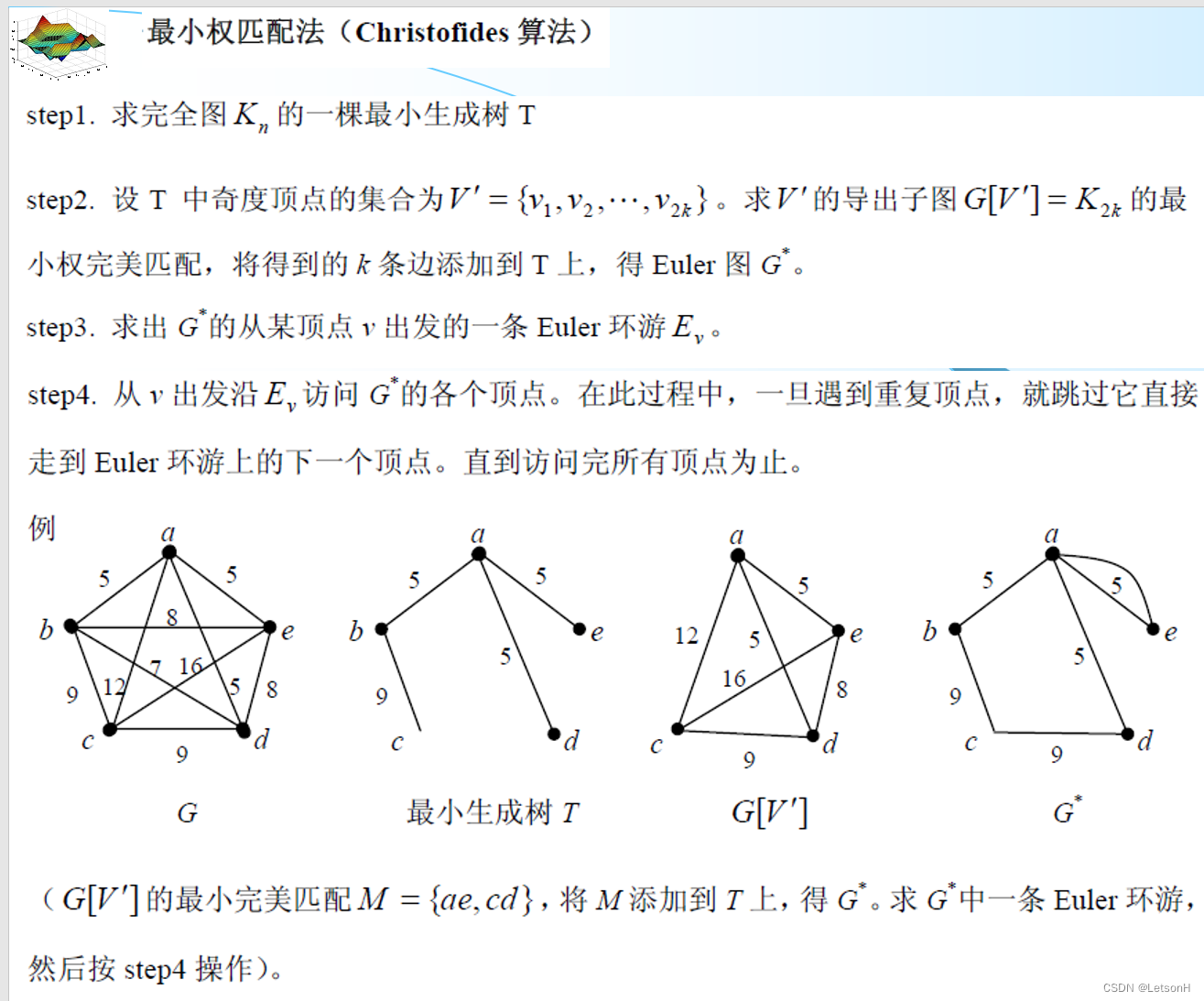
设G=(V,E)是连通无向图。1、巡回:经过G的每边至少一次的闭通路称为巡回。2、欧拉巡回;经过G的每边正好一次的回称为欧拉巡回。3、欧拉图:存在欧拉的图称为欧拉图E图。4、欧拉道路:经过G的每边正好一次的道路称为欧拉道路。
-
设G正好有两个次顶点 u,则沿u到的一条最短路 P(u)加重复边得到 G*,G*的一条欧拉巡回便是 G的最佳巡回。
-
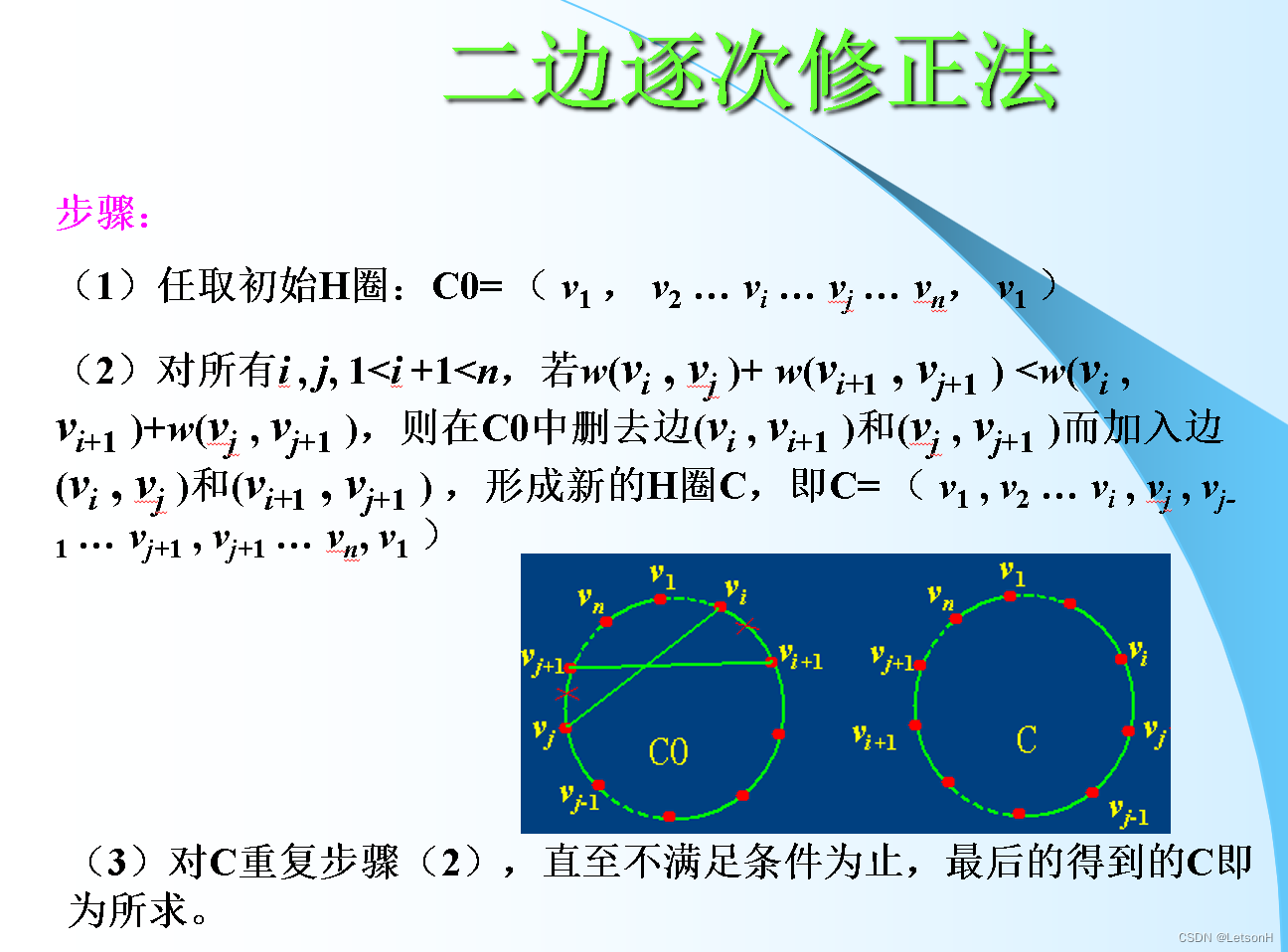
经过图G每个顶点正好一次的路径为G的一条哈米尔路径简称H路径。经过G的每个顶点正好一次的圈,称为G的哈米尔顿圈或H圈。含H圈的图称为哈米尔顿图或H图。
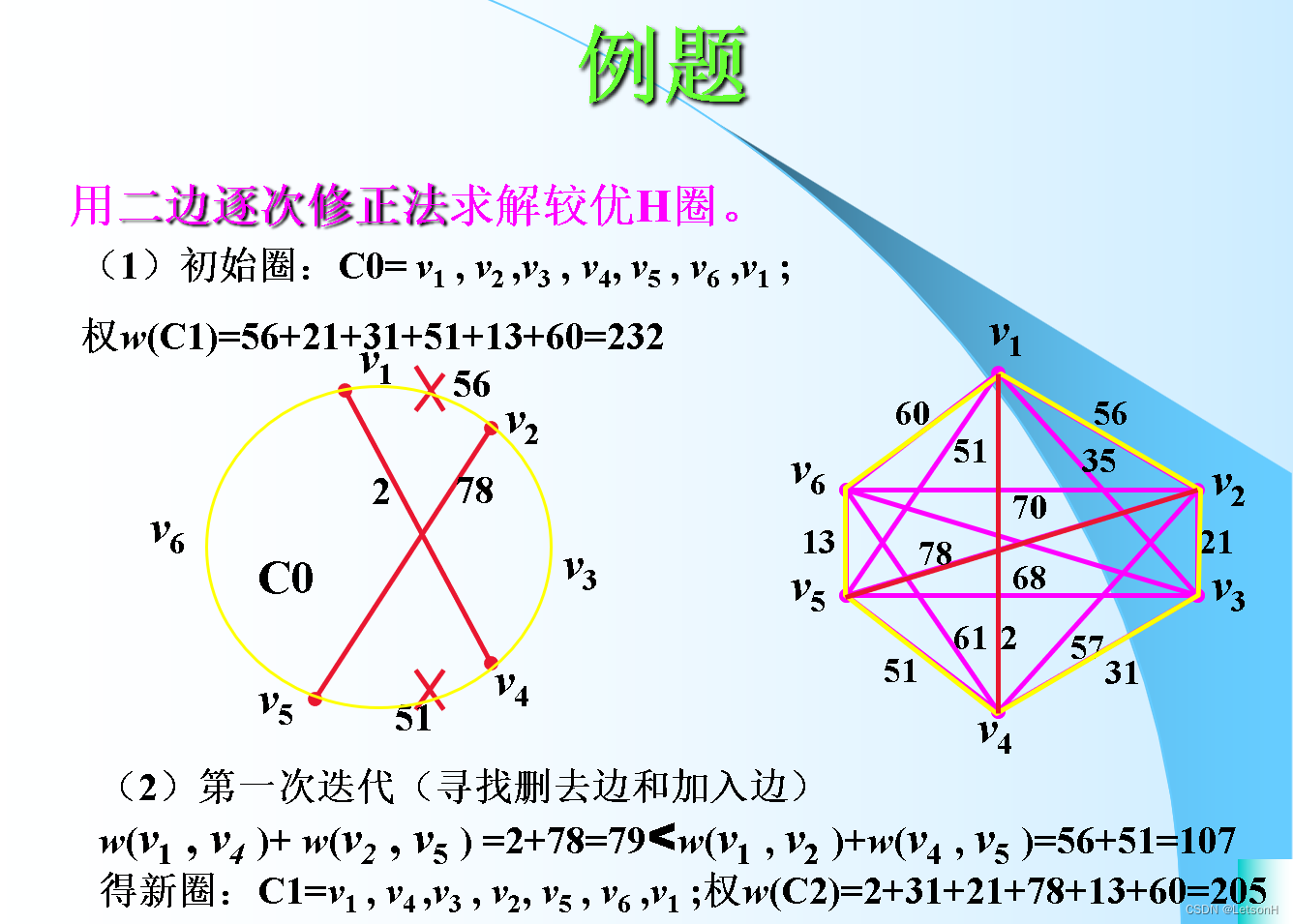
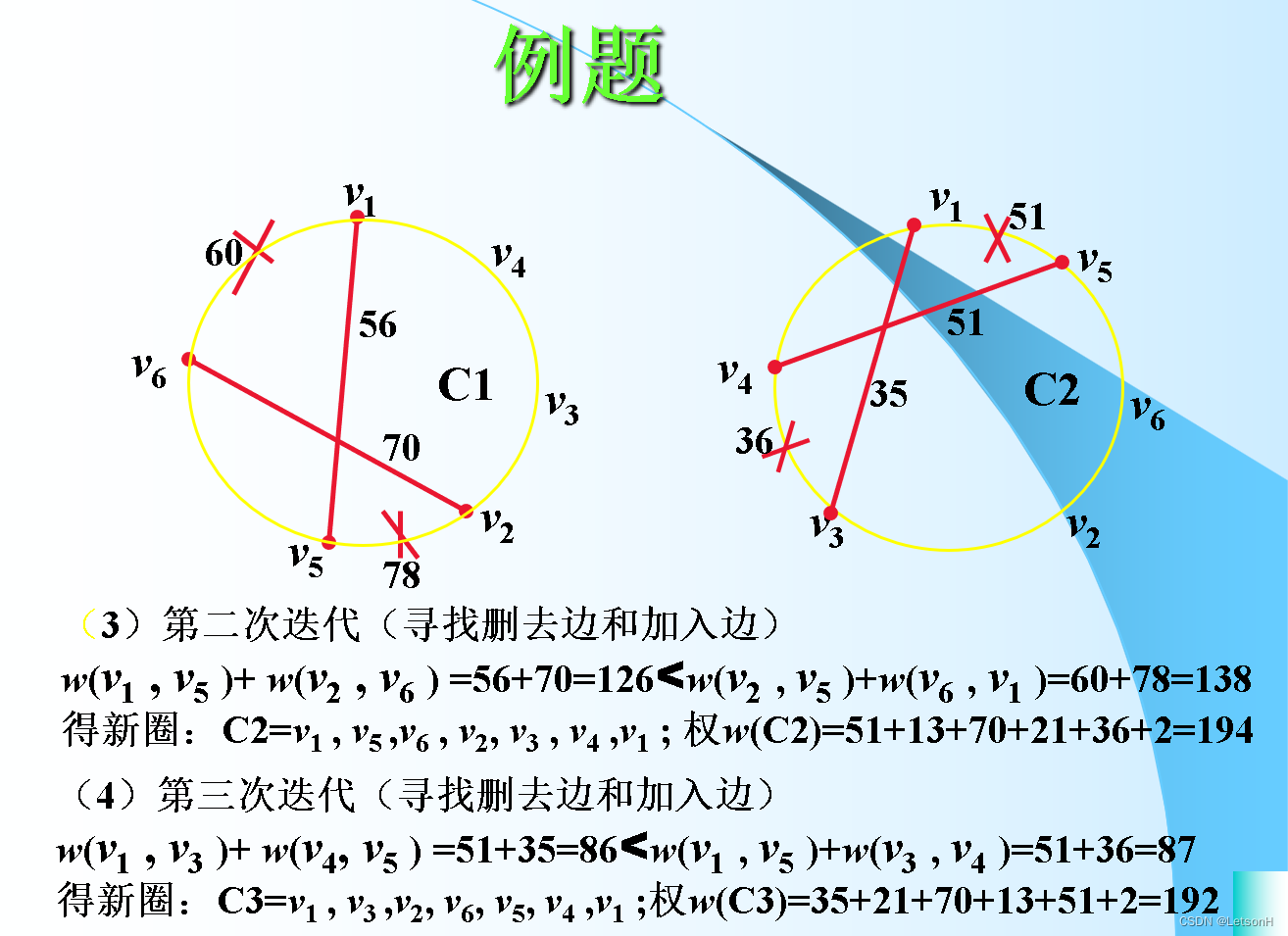
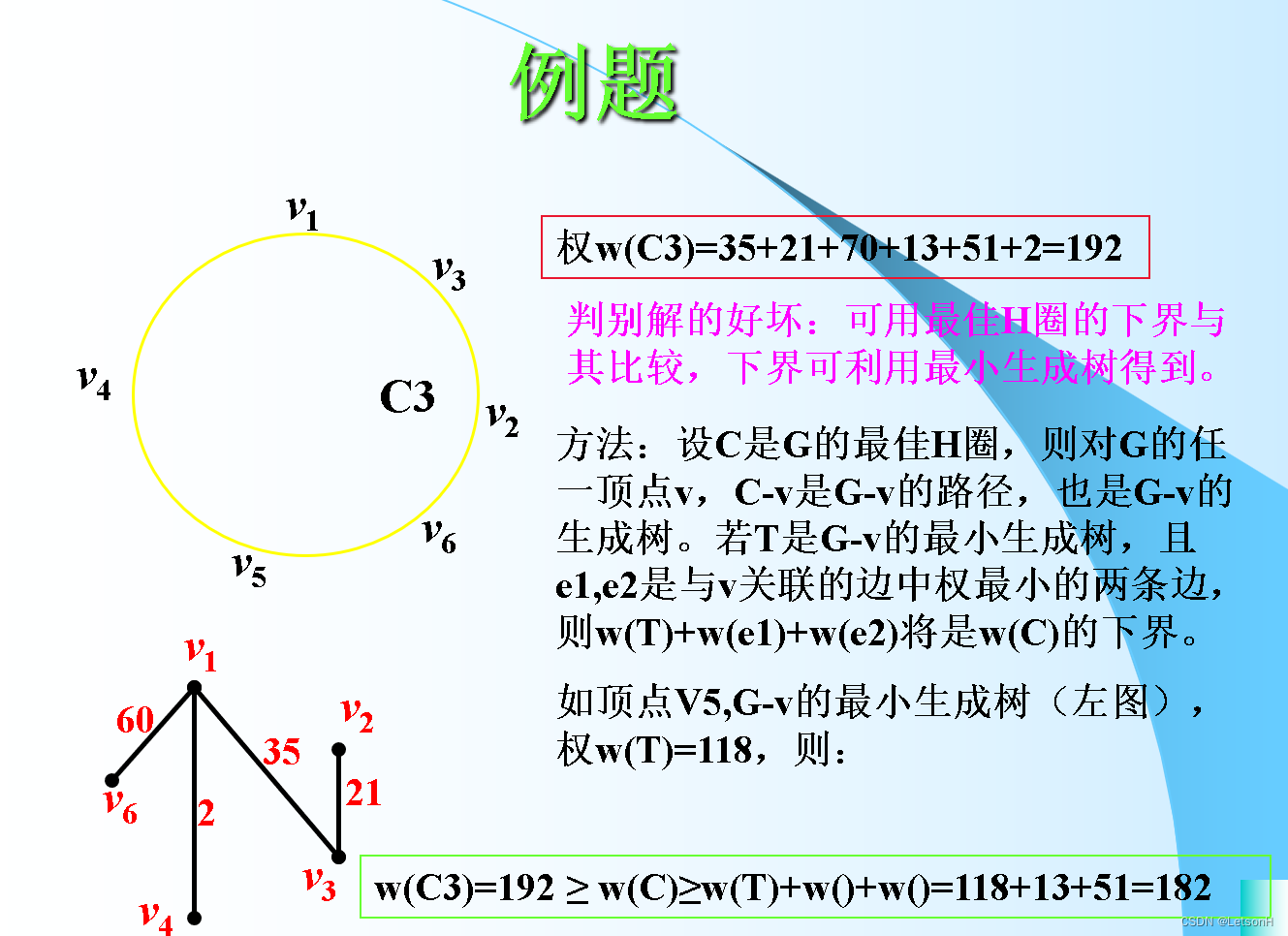
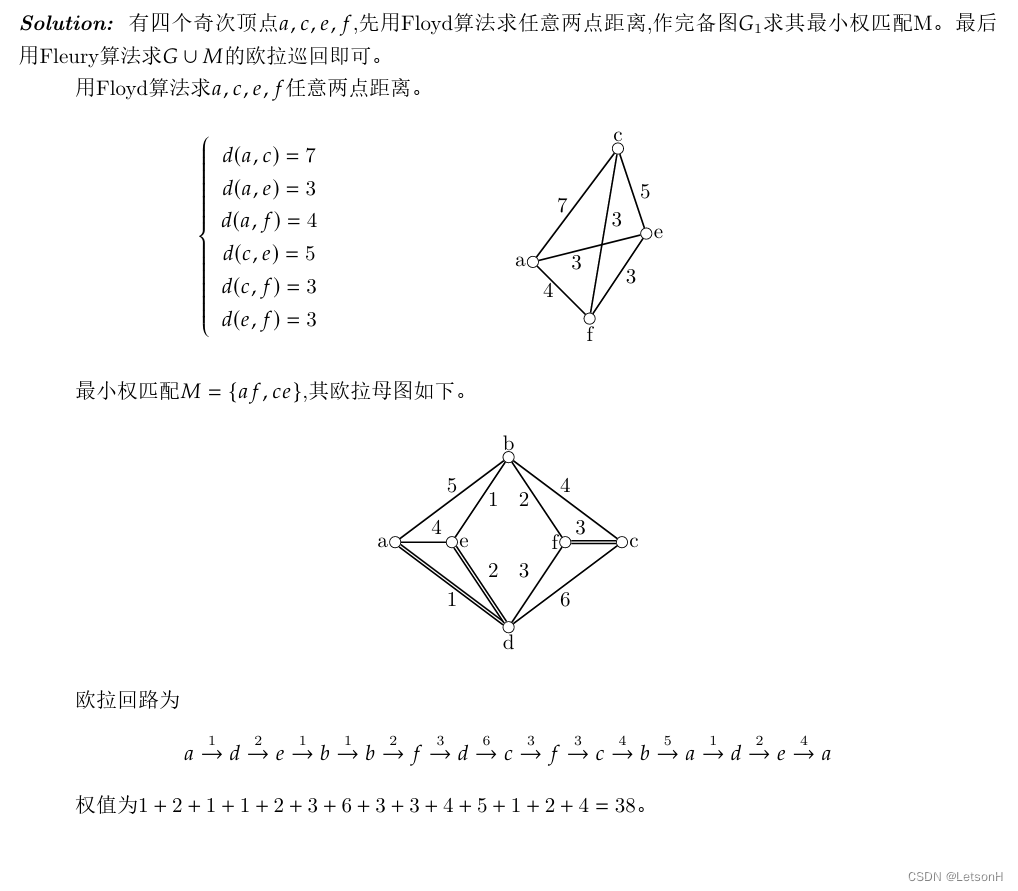
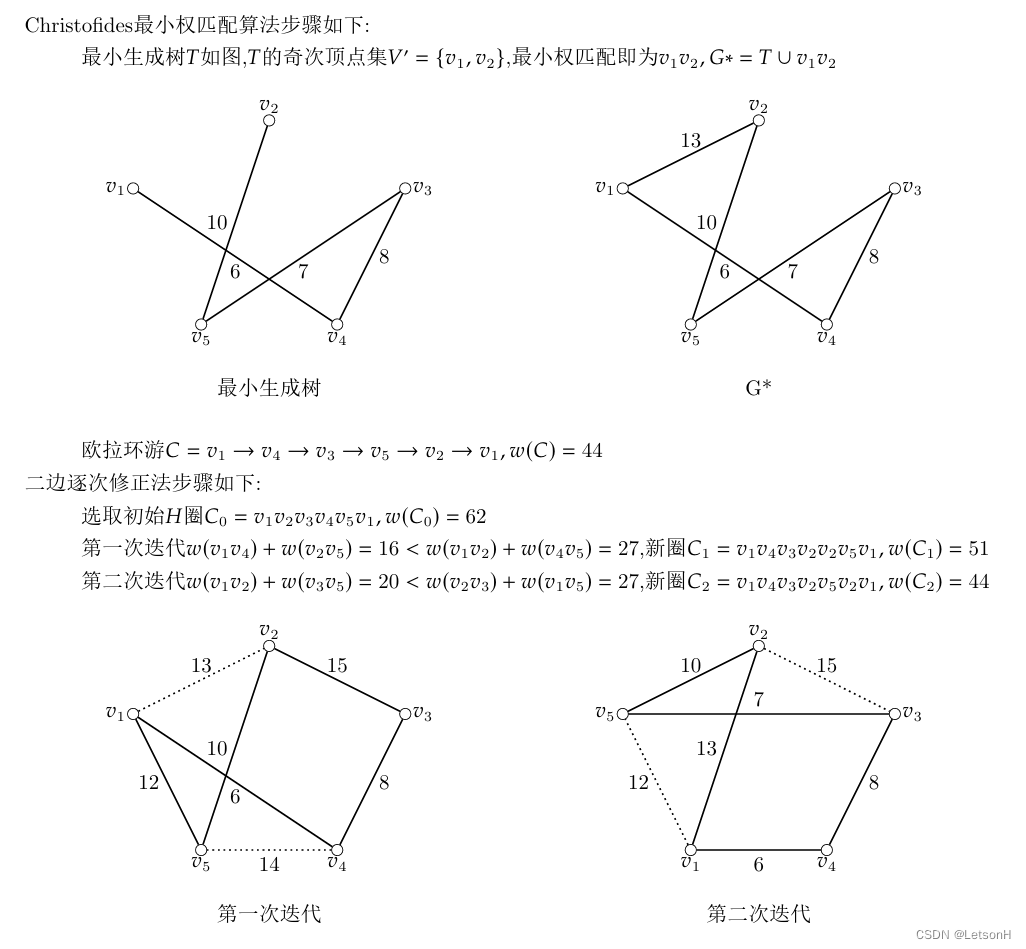
计算







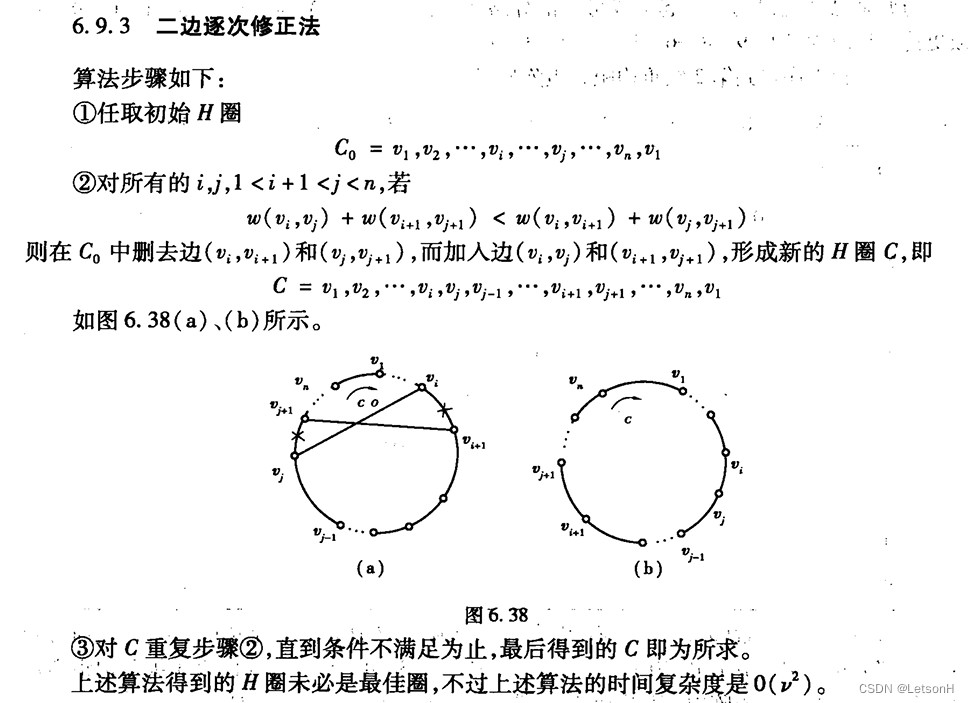
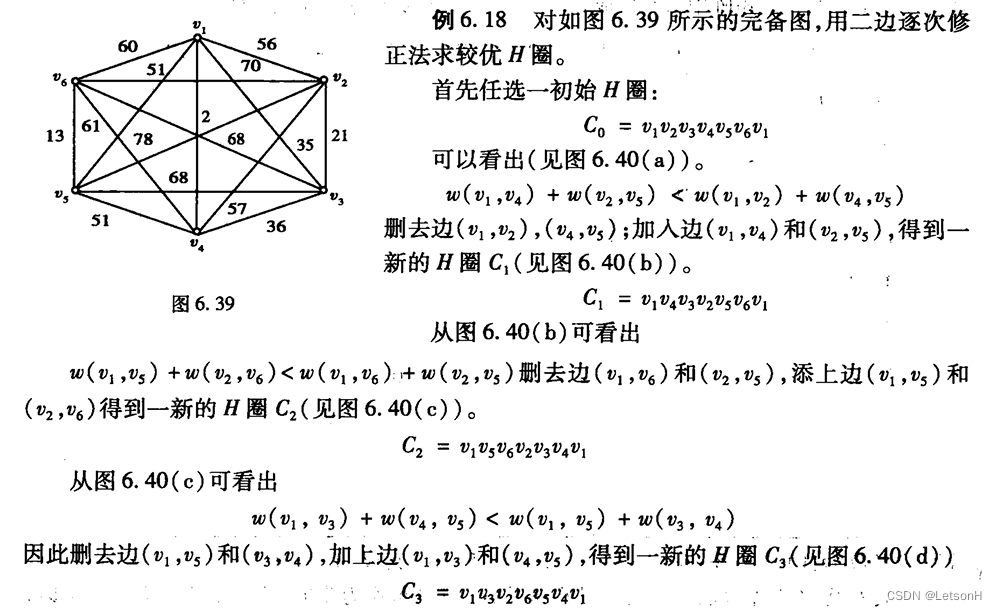
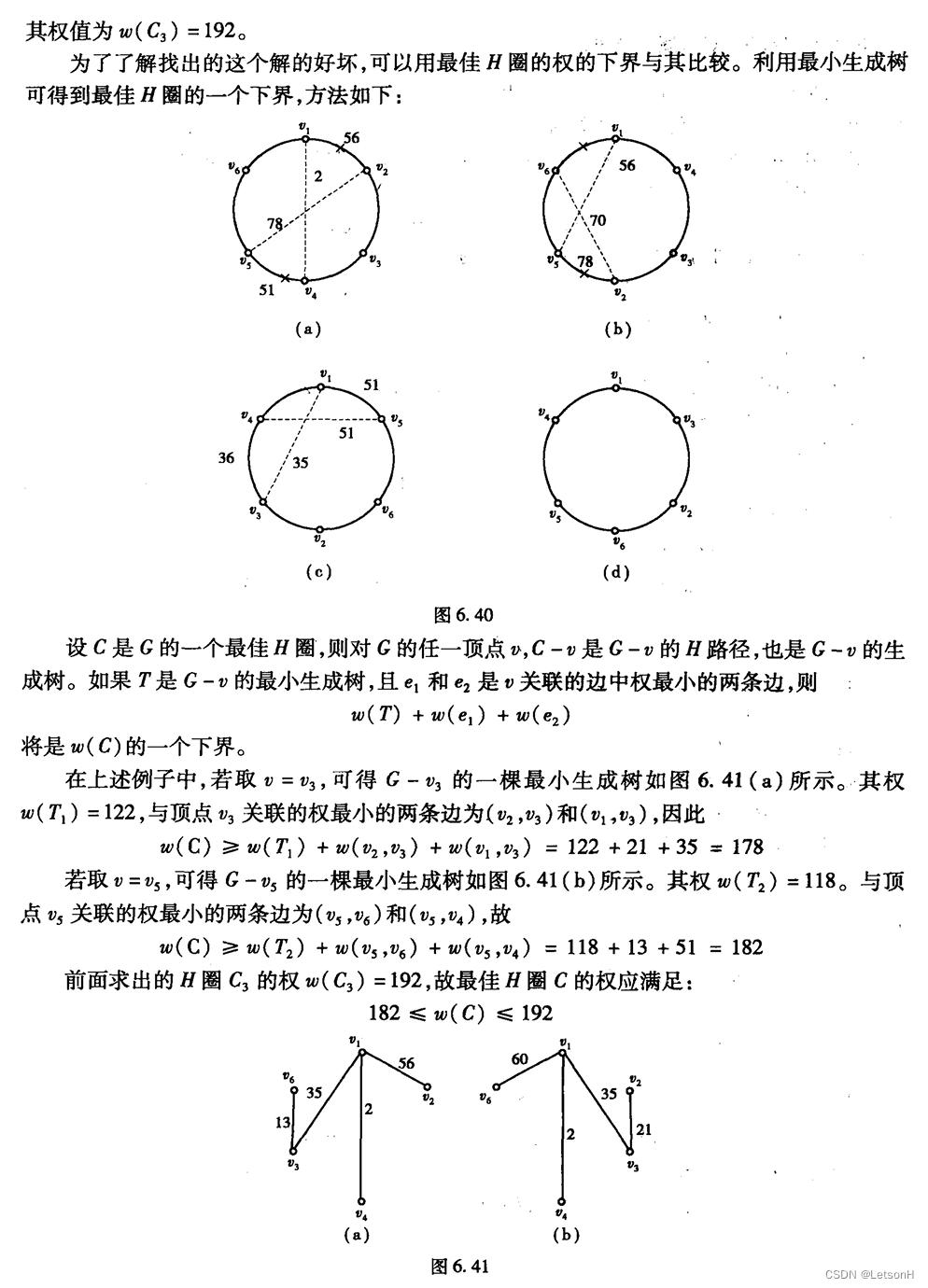
作业


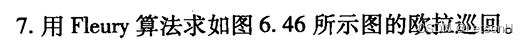
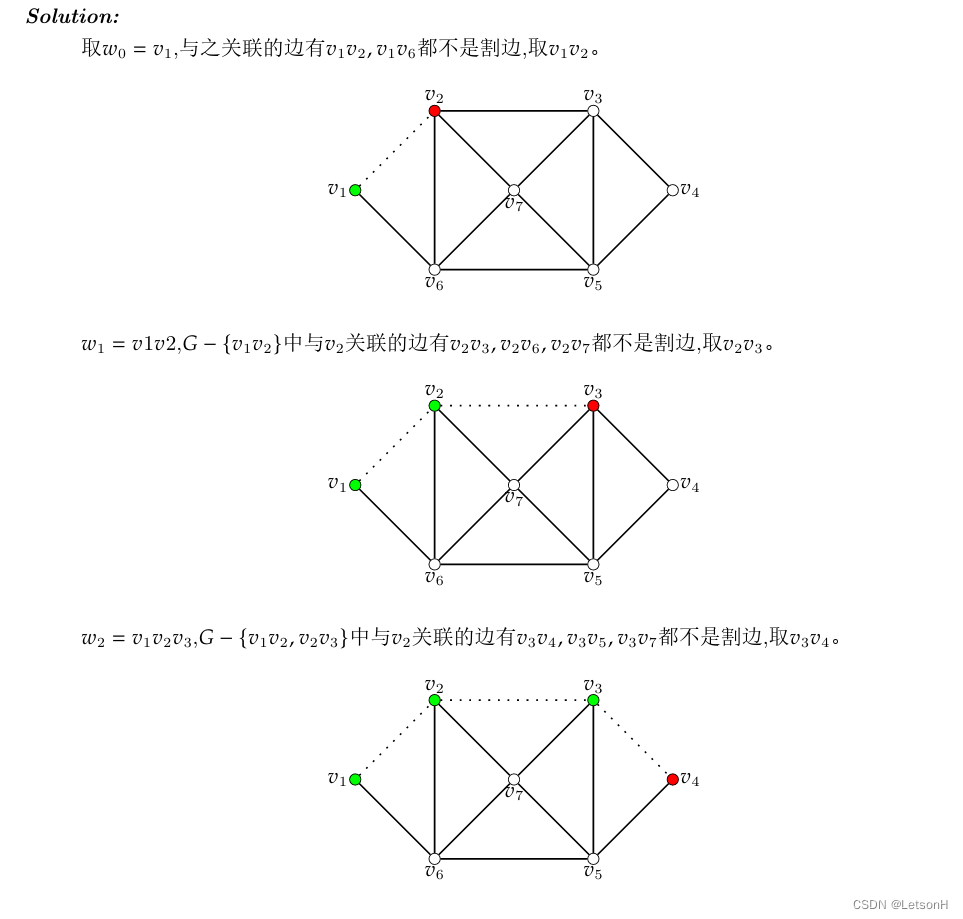
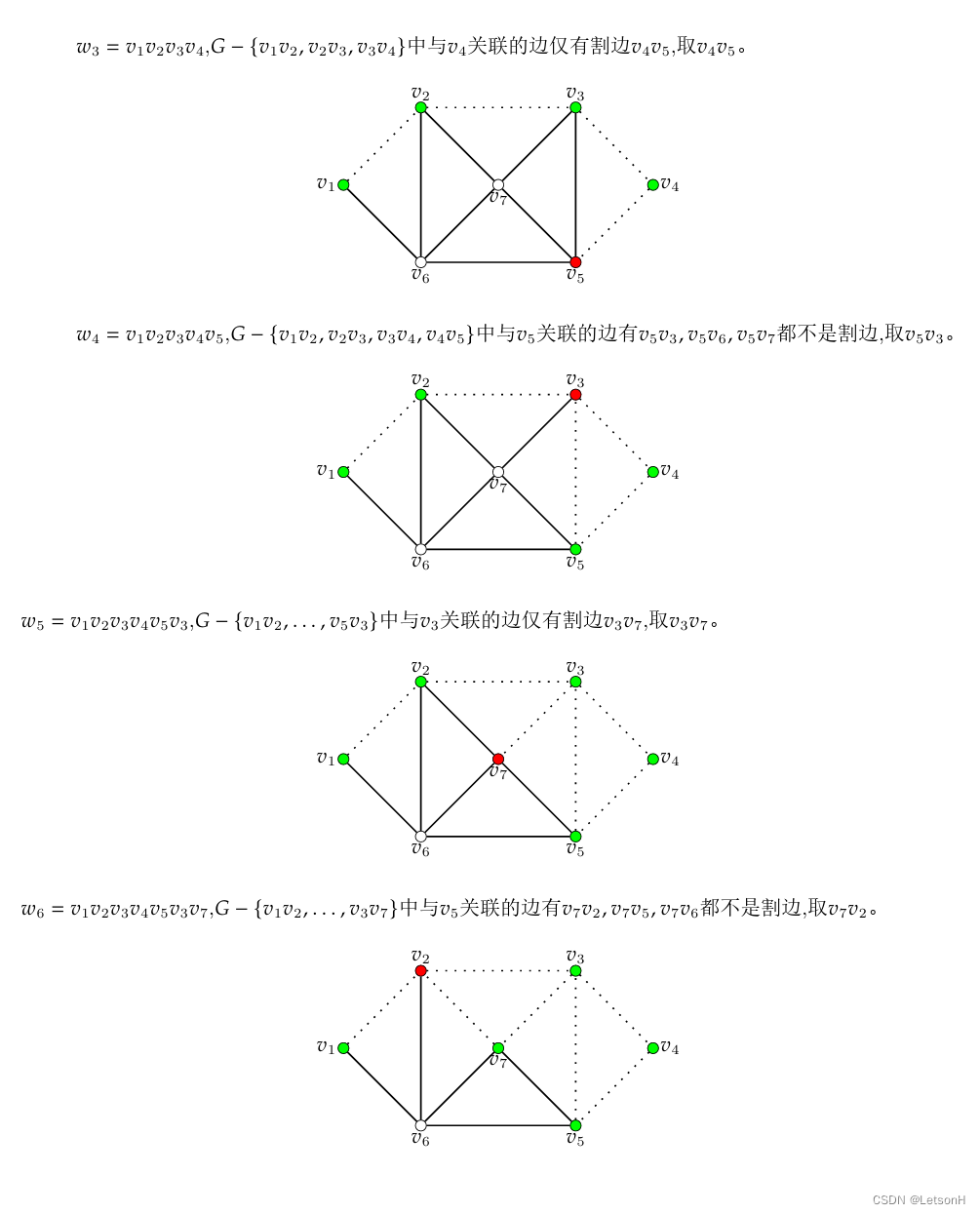
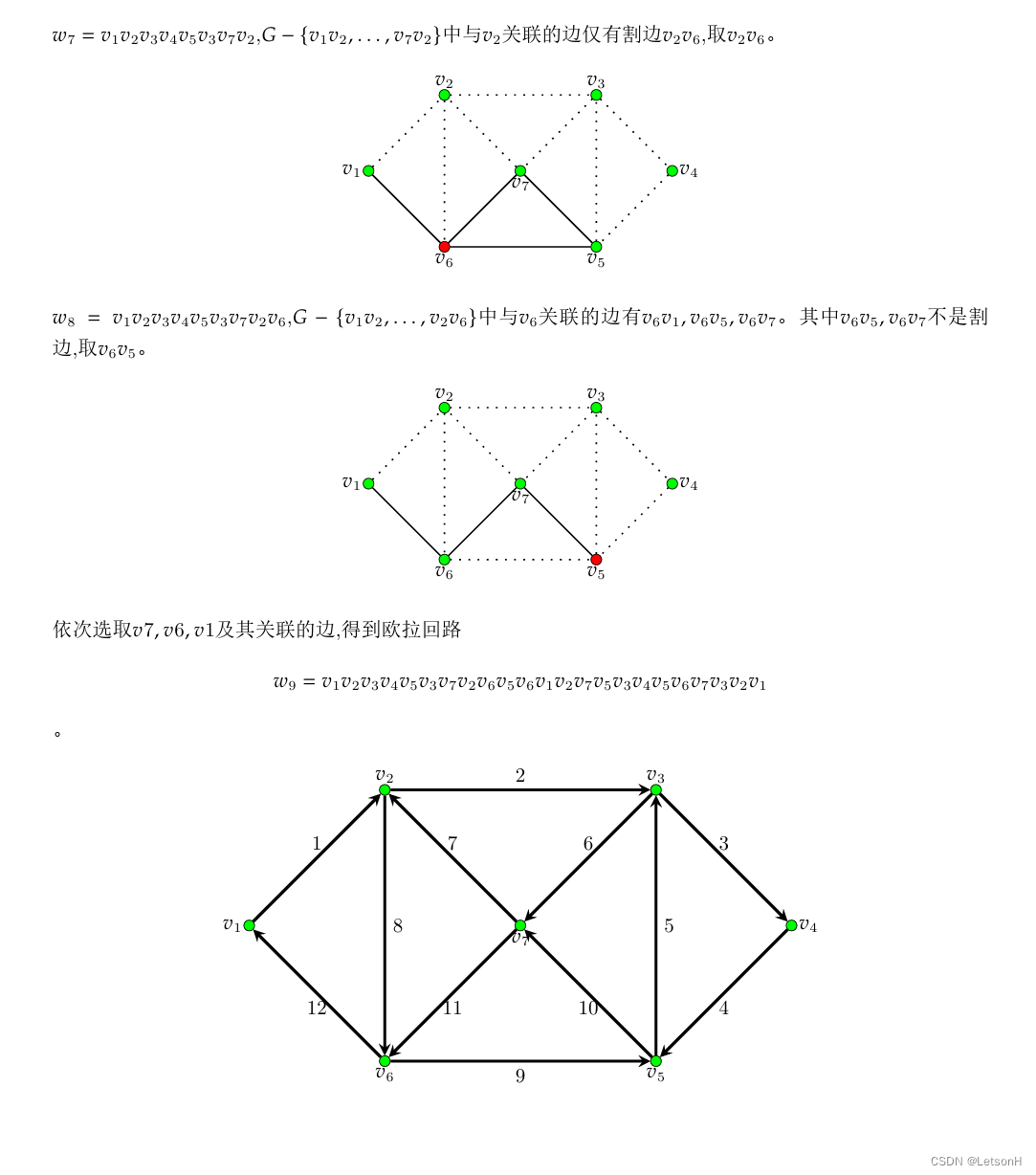
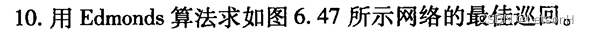
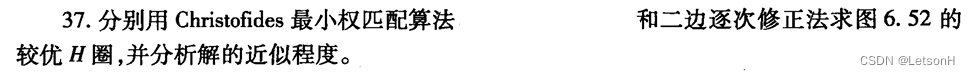
第七章:7.1、7.2、7.3、7.4、7.5
填空
-
设G=(n, m)是平面图,则:
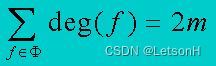
-
(欧拉公式) 设G=(n, m)是连通平面图,ф是G的面数,则:

-

-
设G是平面图G的对偶图,则它们的边数(G)、(G),顶点数(G)、(G)和面数(G)、 (G)之间必满足关系式【G的顶点数等于G的面数;G的边数等于G的边数;G的面数等于G的顶点数;d (v)=deg( f )】**
-
平面图G的对偶图必然连通
-
G是平面图,则
 当且仅当G是连通的。
当且仅当G是连通的。 -
同构的平面图可以有不同构的对偶图。
-
库拉托夫斯基定理:图G是非可平面的,当且仅当它含有K5或K3,3细分的子图
-
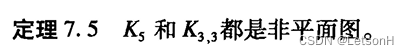
-

-
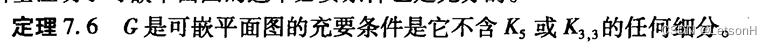
-

计算



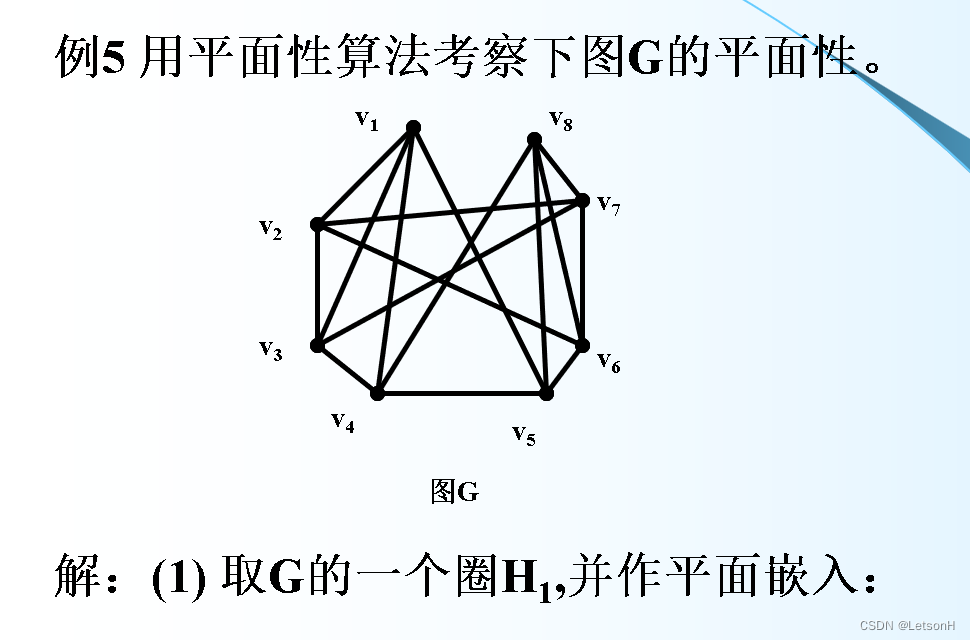
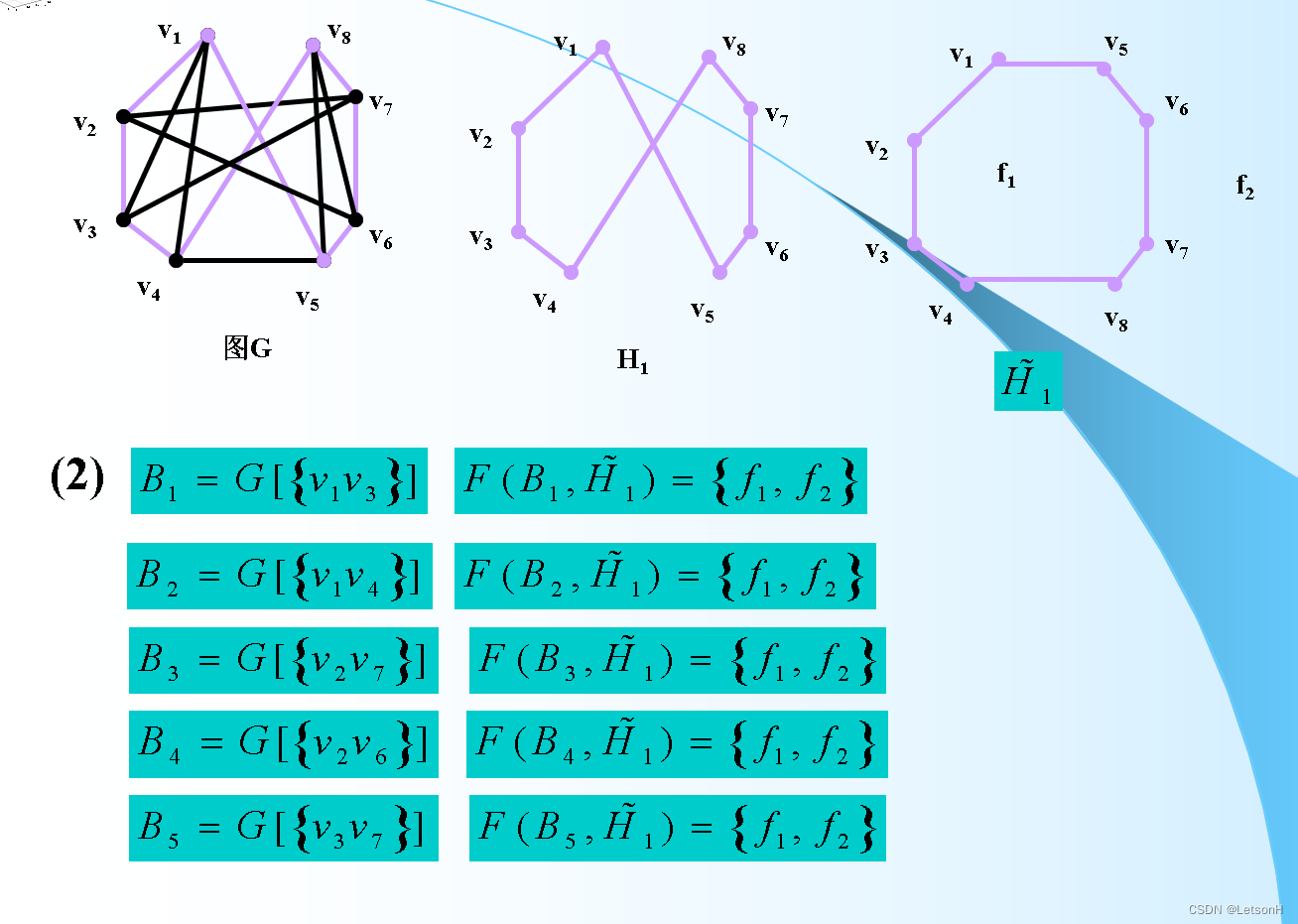
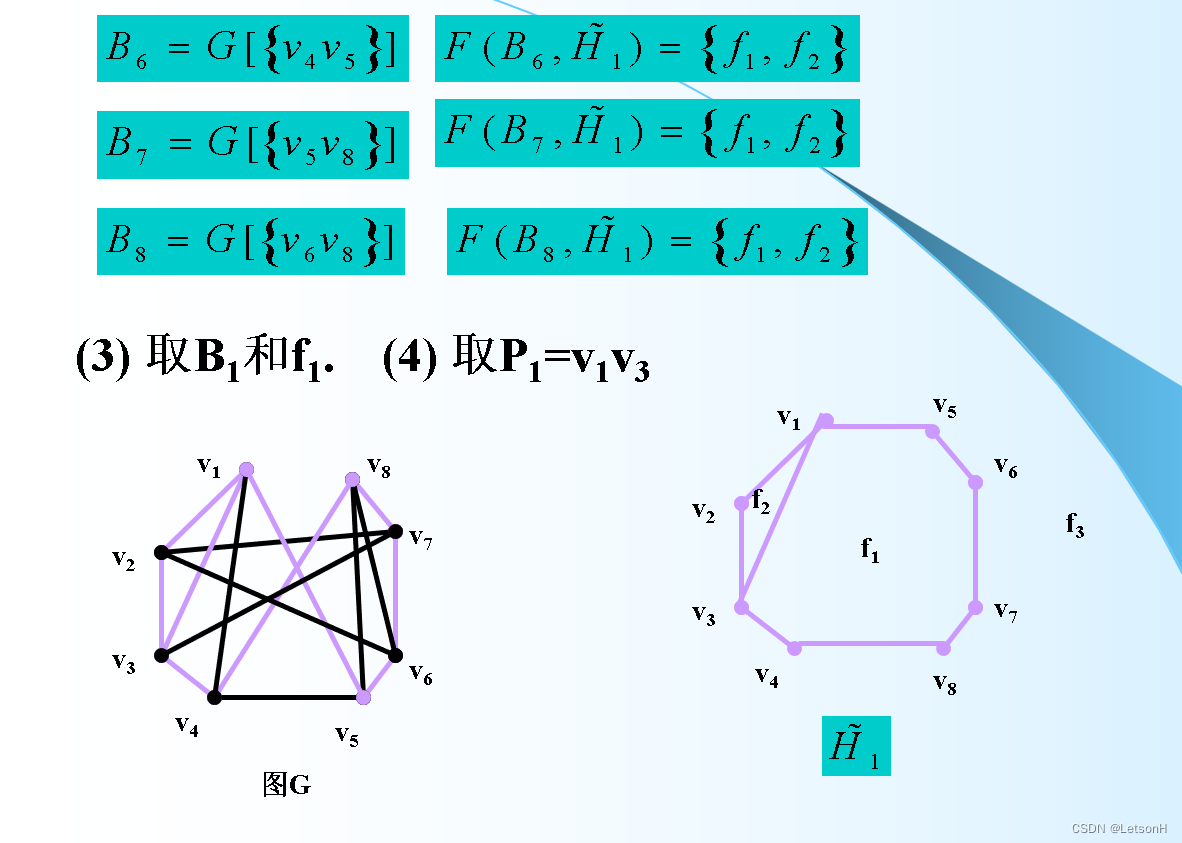
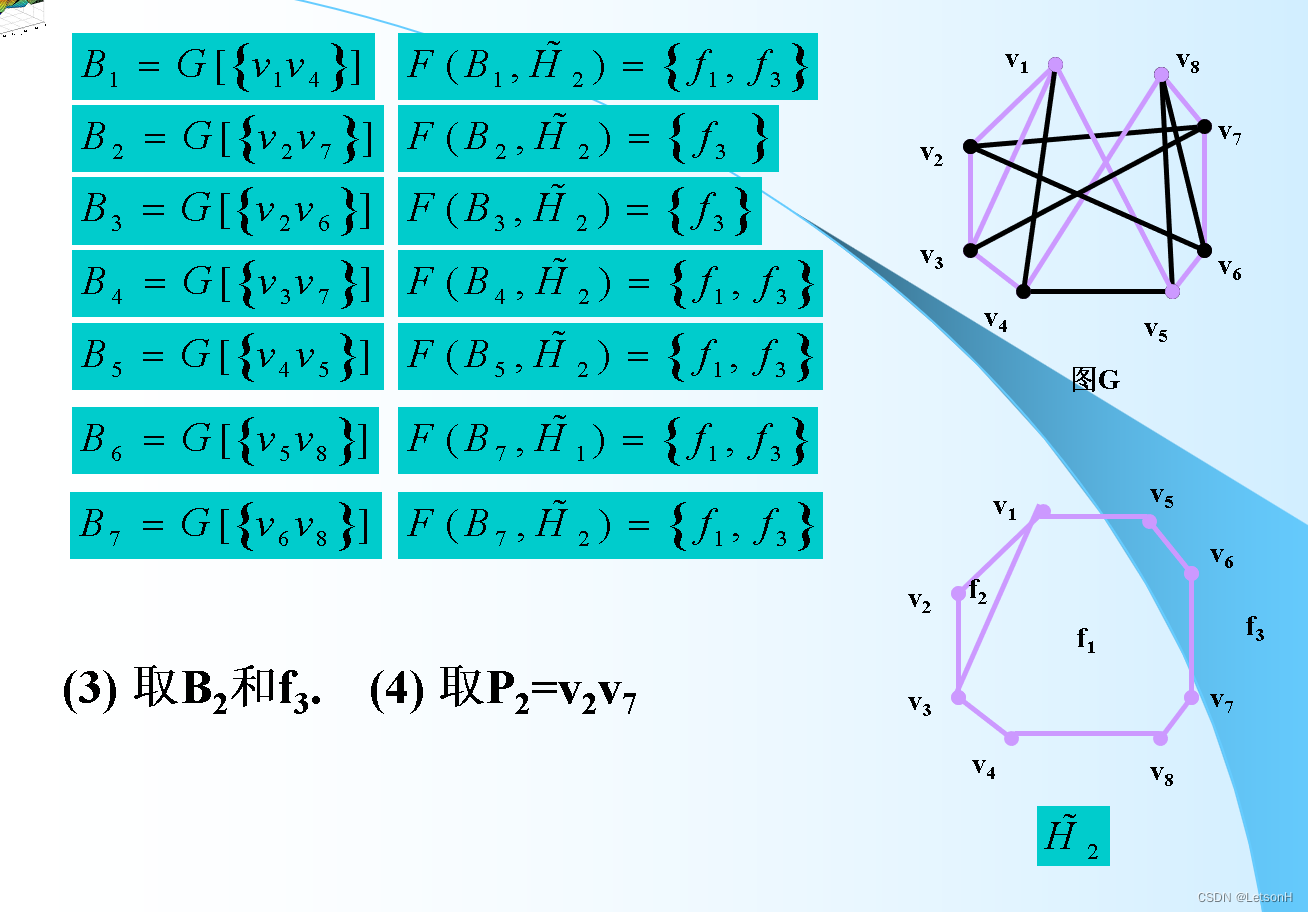
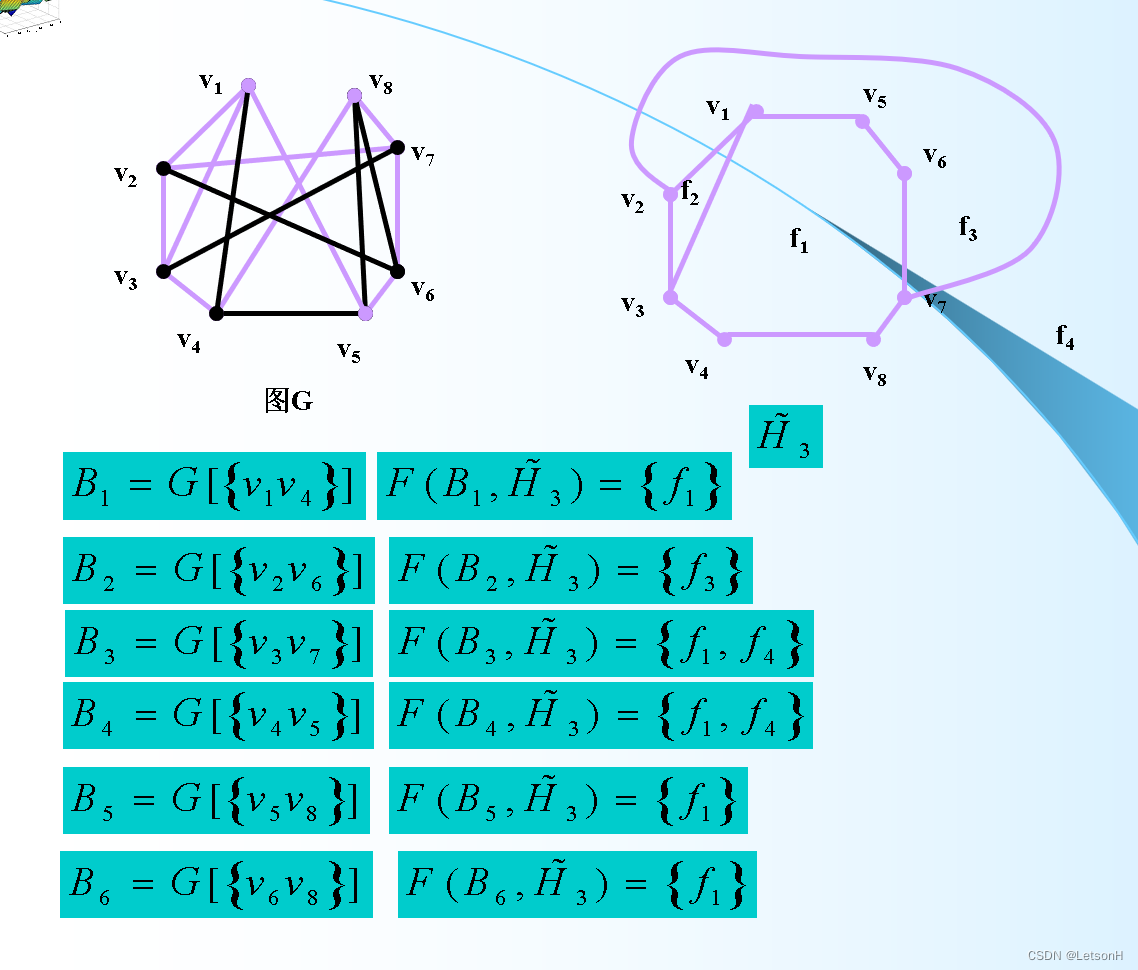
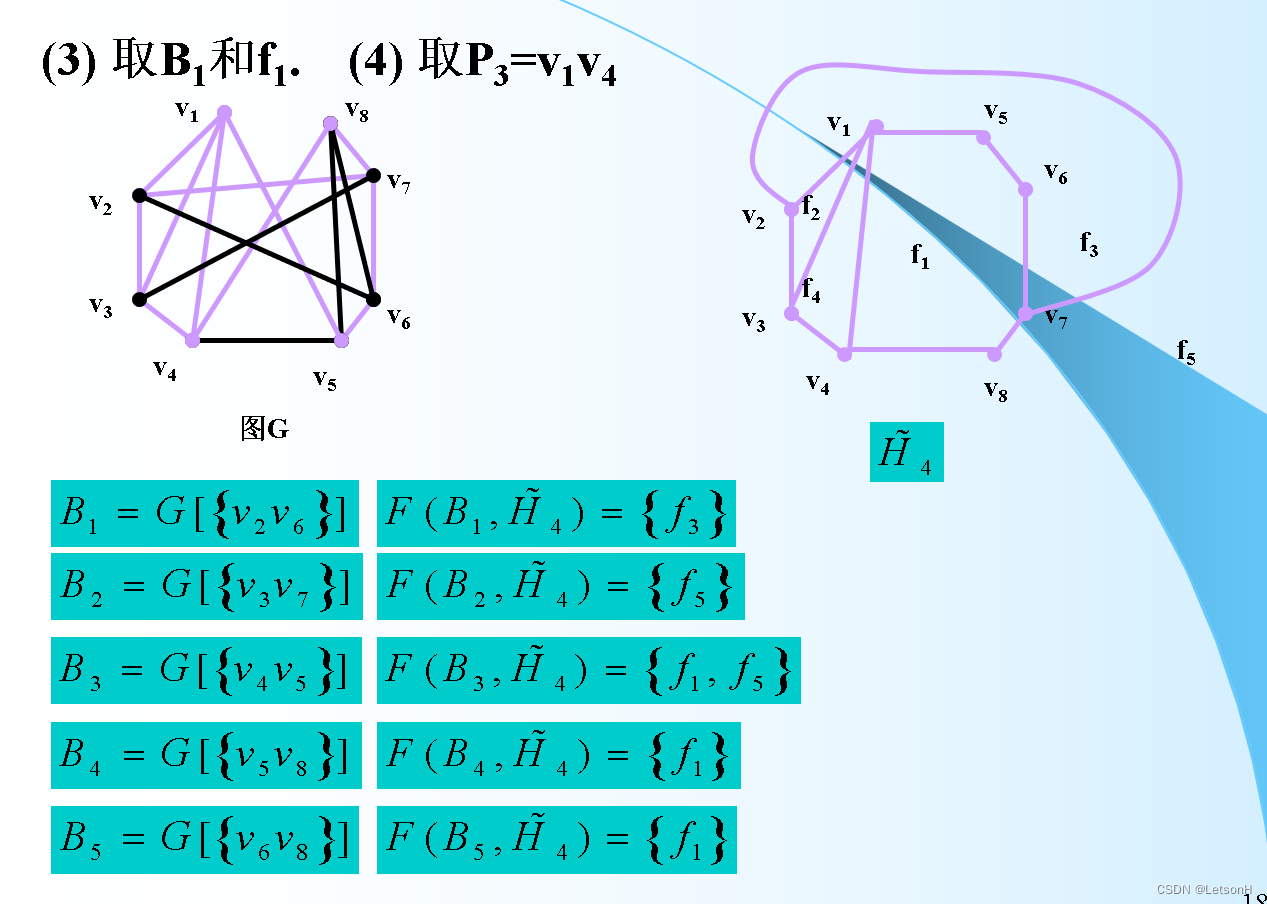
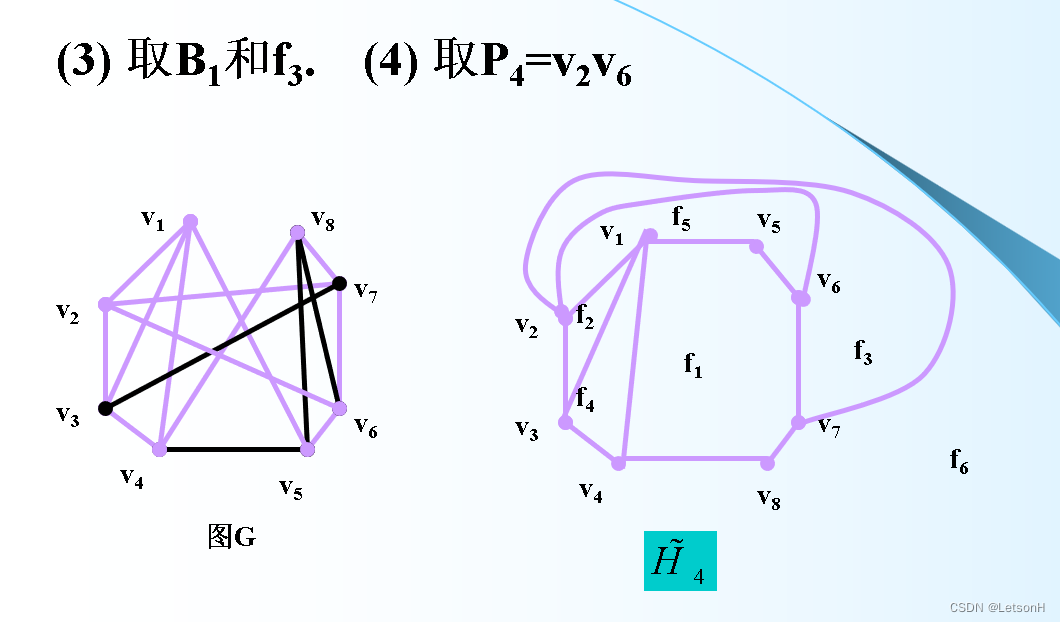
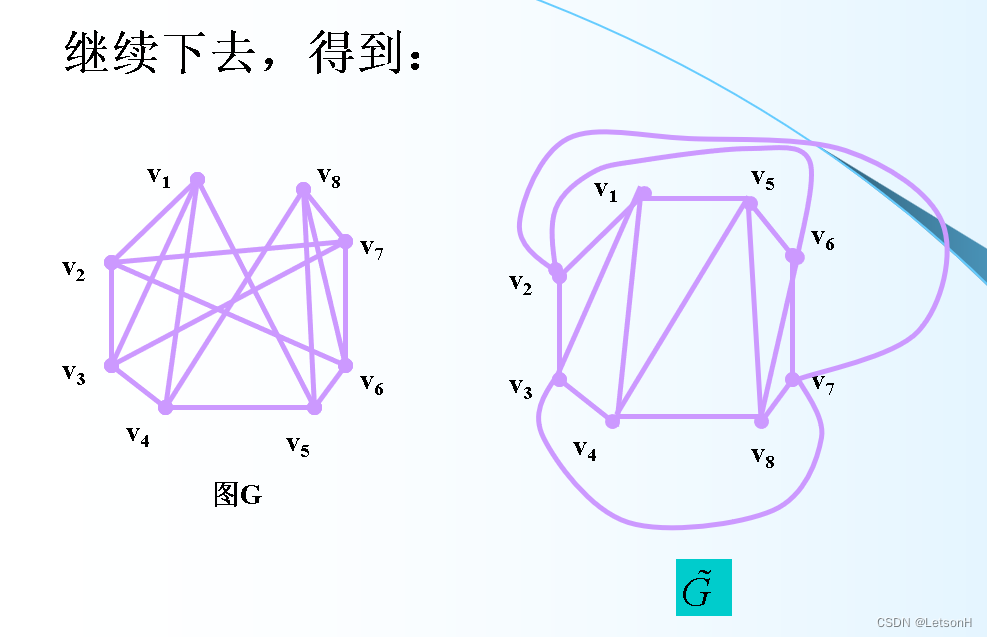
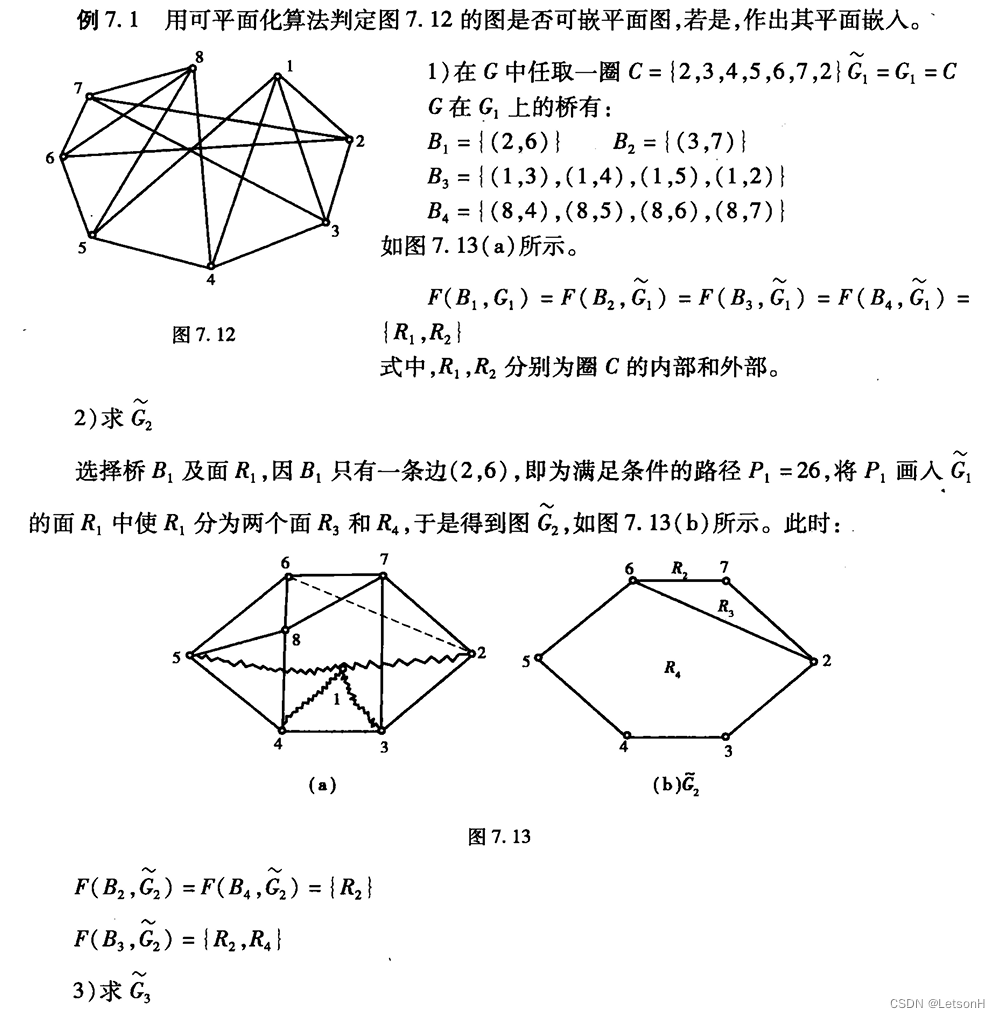
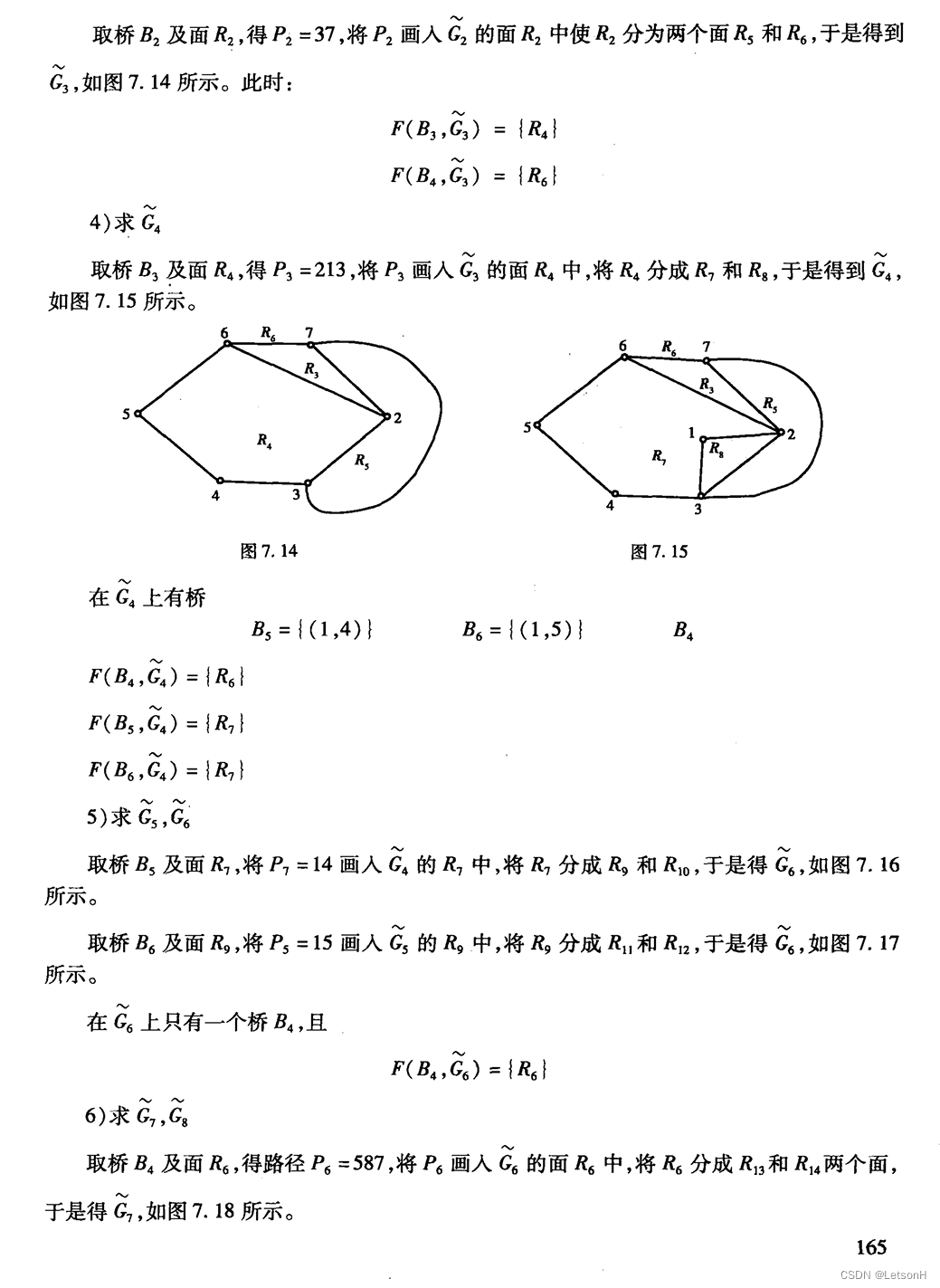
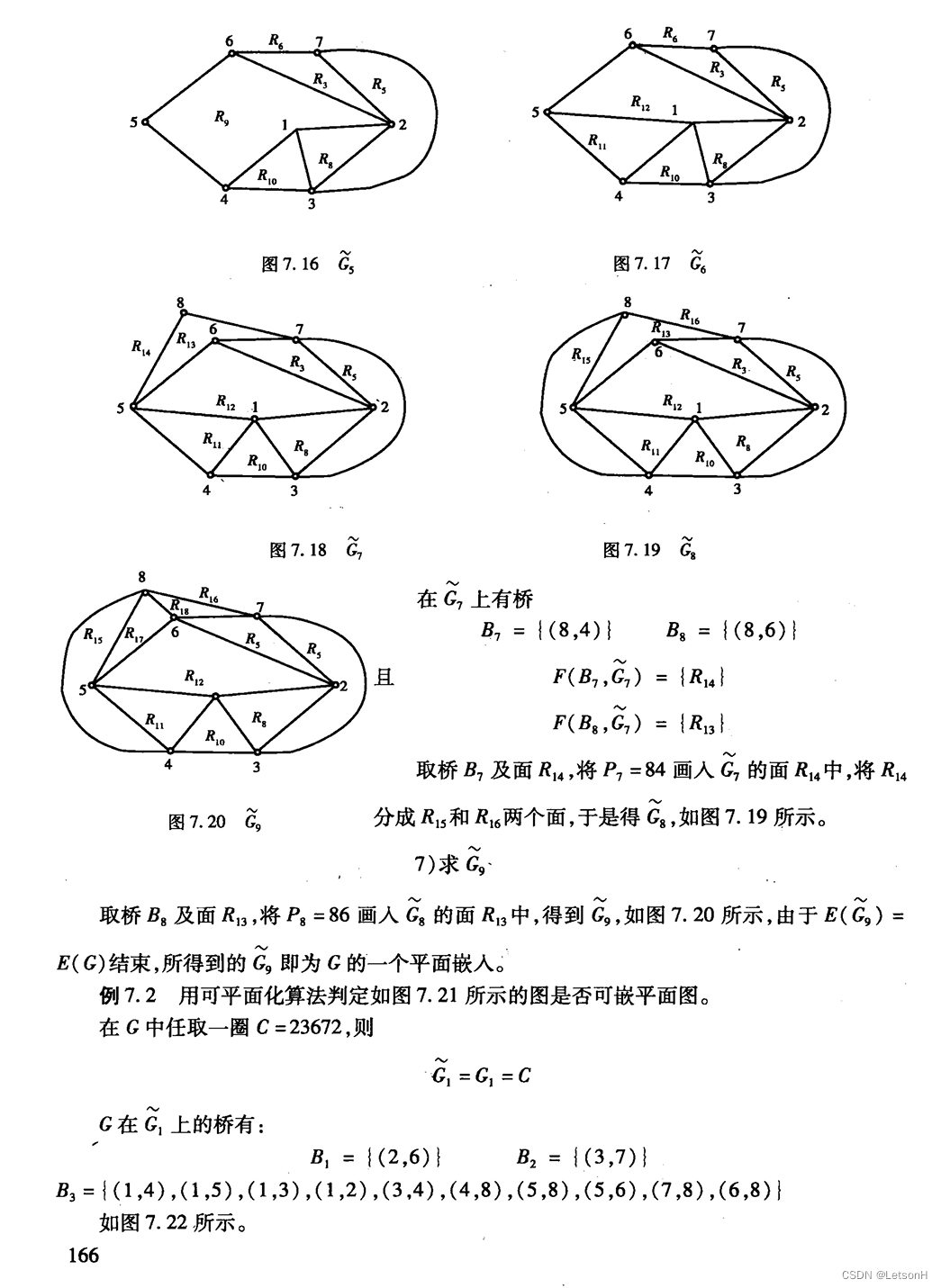

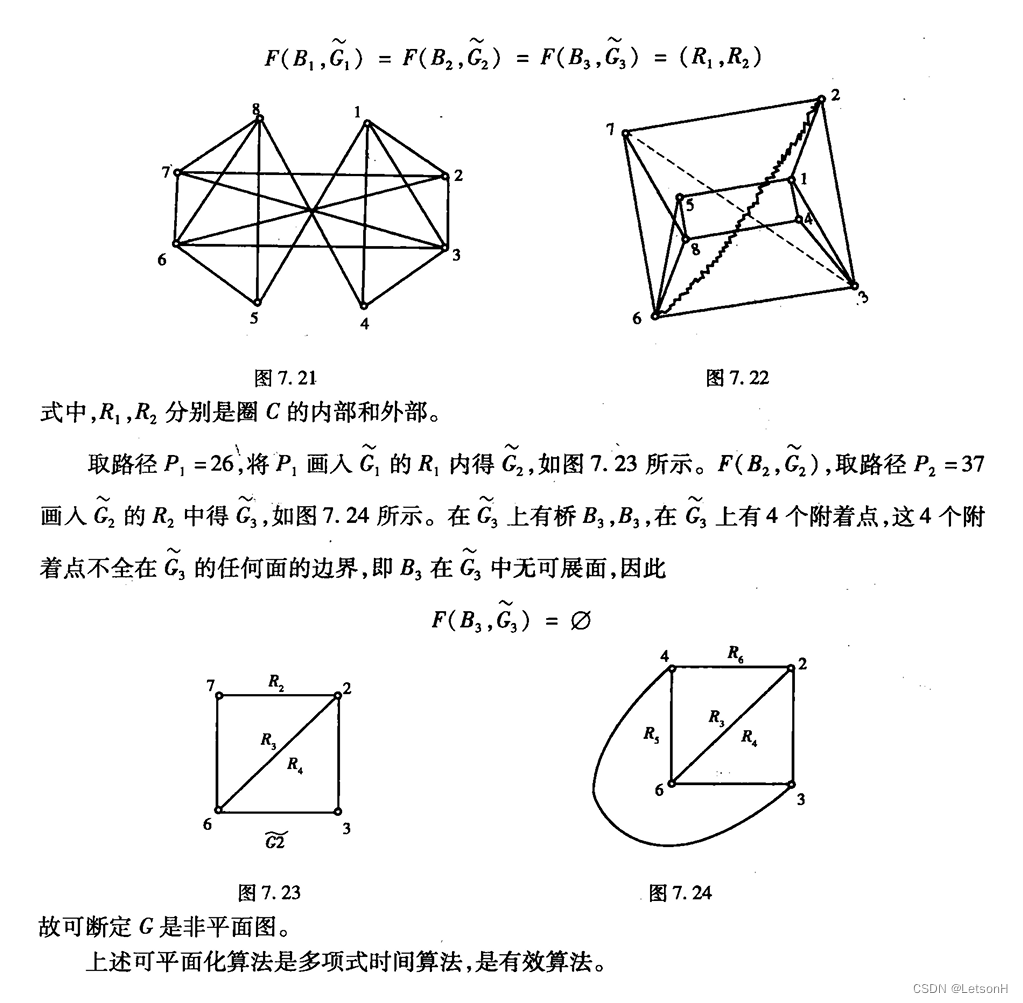

作业




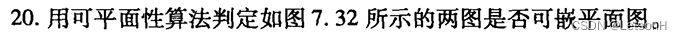
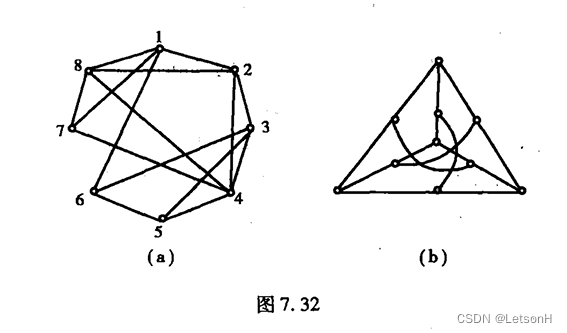
历年真题1
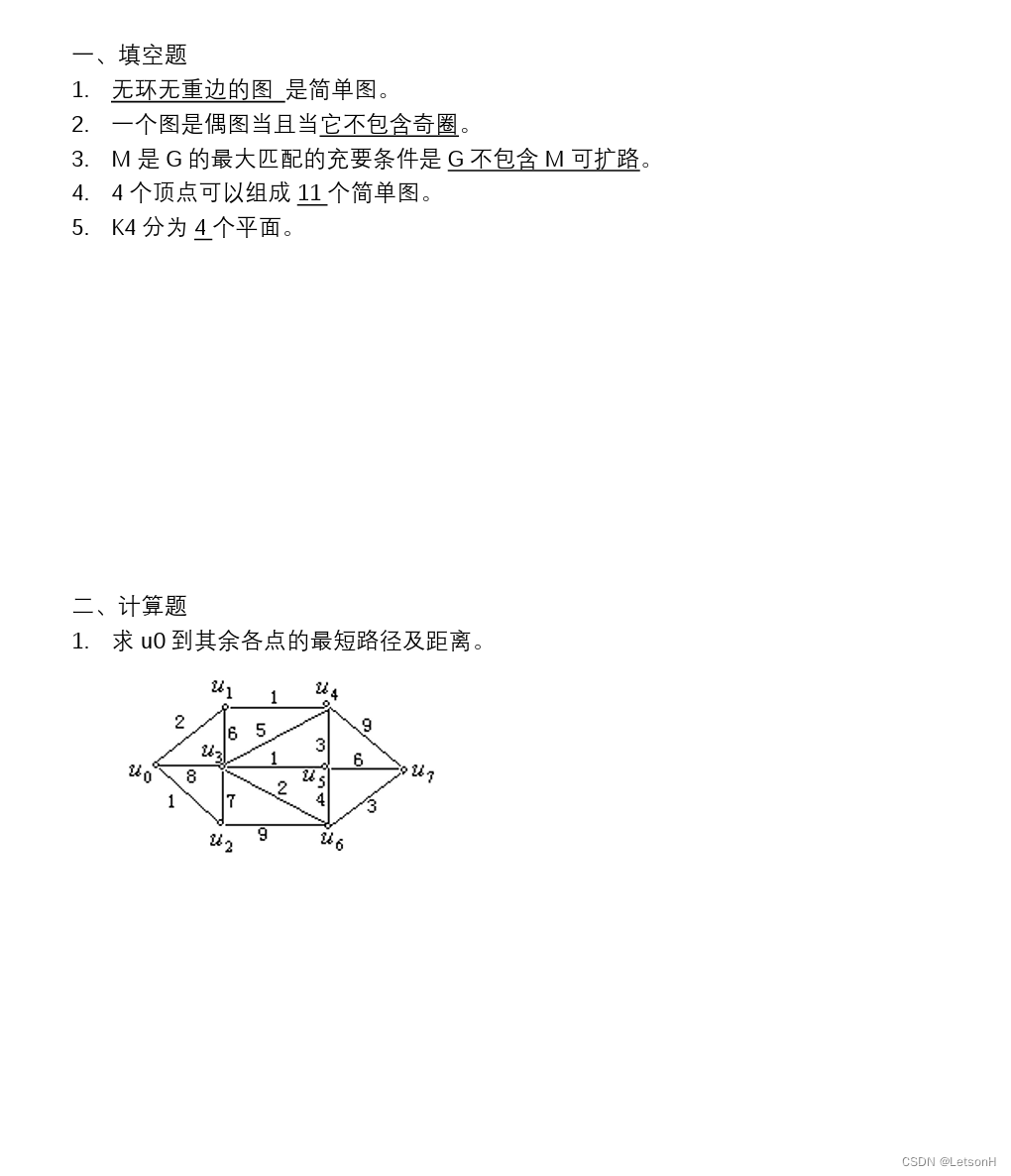
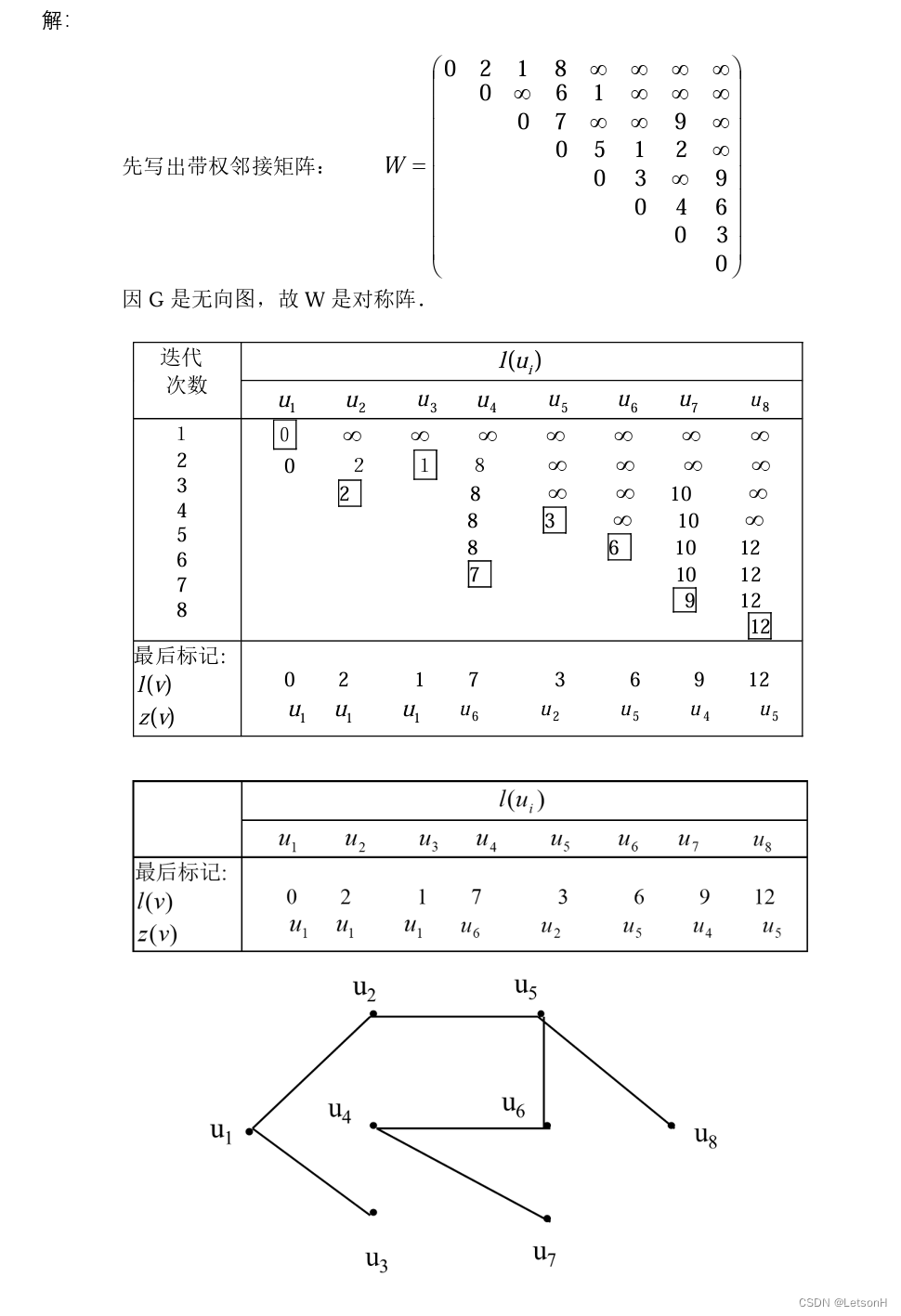
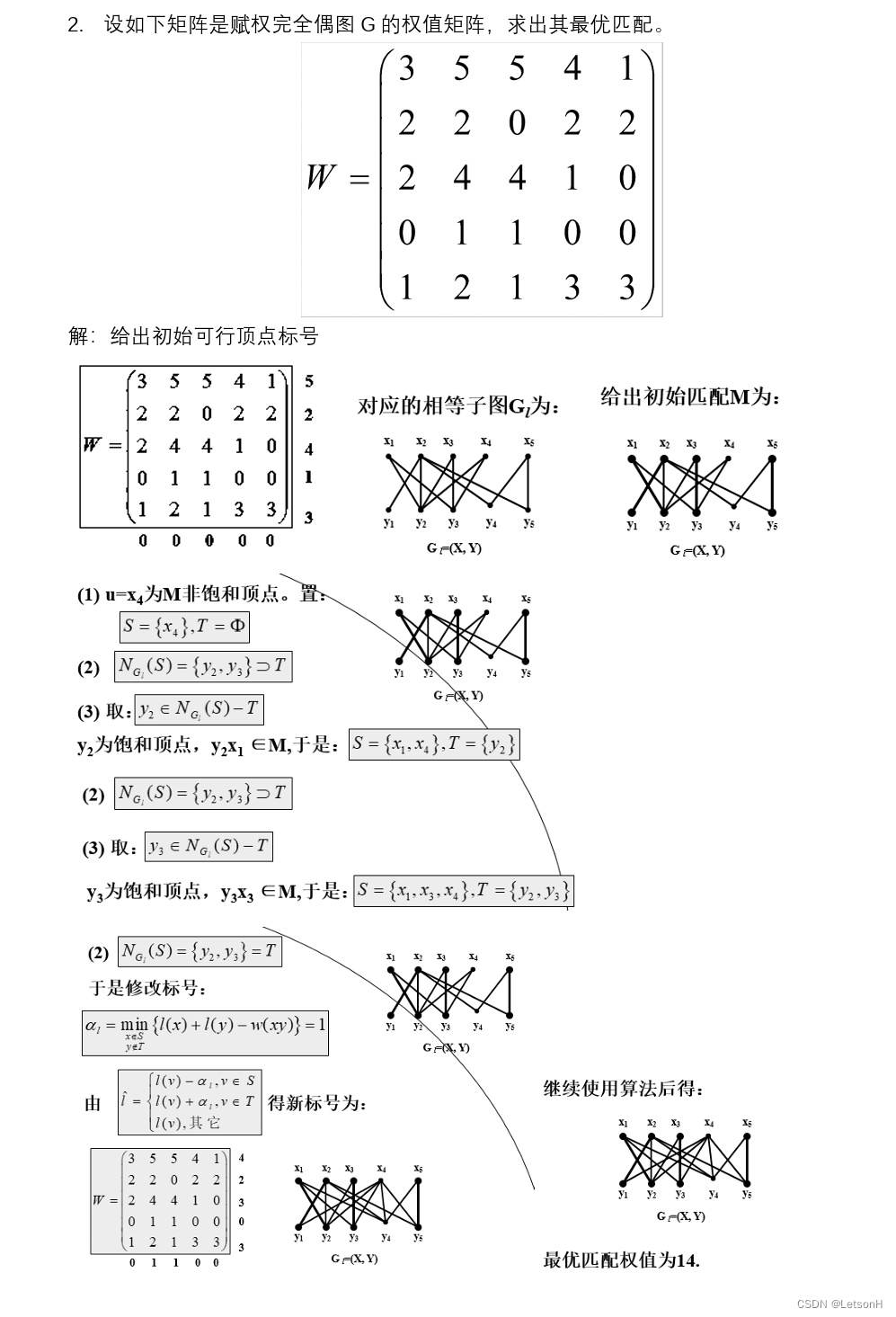
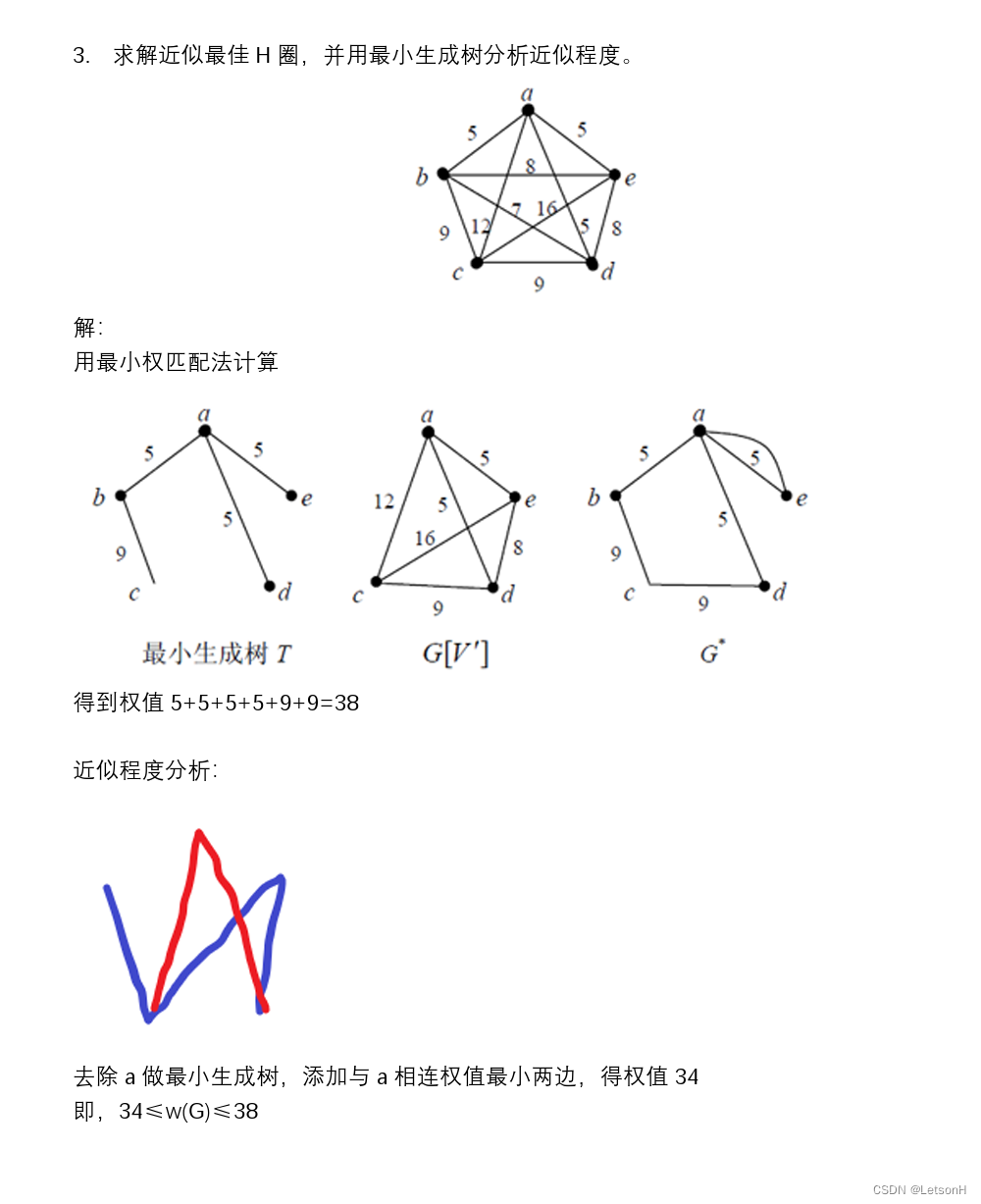
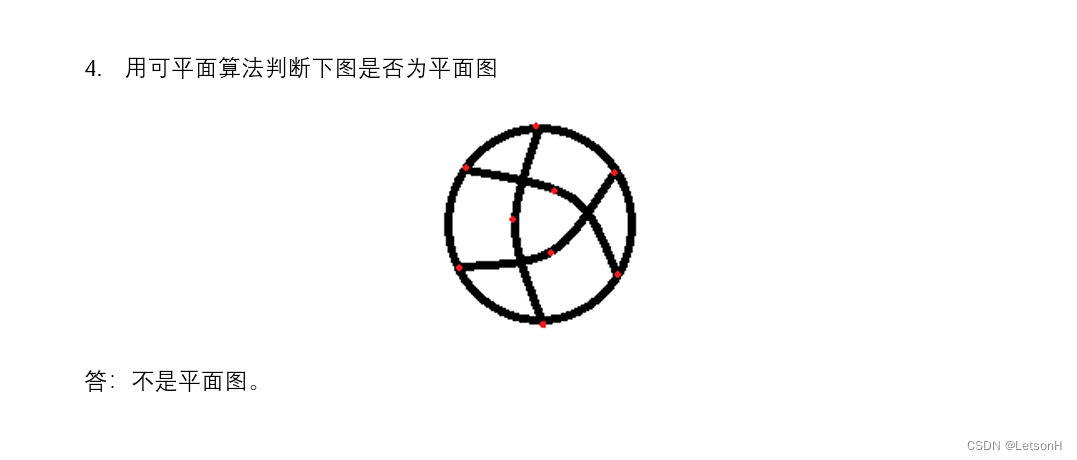

历年真题2

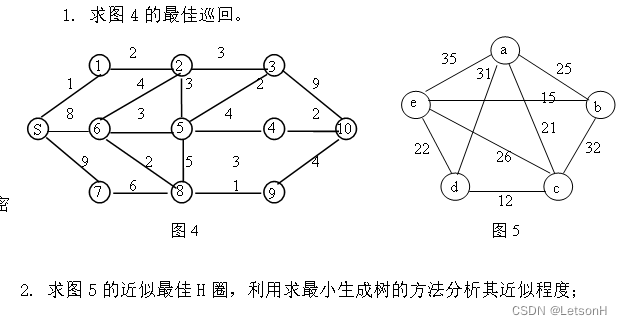

历年真题3
填空题20分
1.非平凡树至少有多少个一次顶点。
2.K5,6的最小覆盖是几5
3.库拉托夫斯基定理:图G是非可平面的,当且仅当它含有K5或K3,3细分的子图
4.门格尔定理
设x和y是图G中的两个不相邻点,则G中分离x和y的最少点数等于独立的(x, y) 路的最大数目。
设x和y是图G中的两个不同点,则G中分离x和y的最少边数等于边不重的(x, y) 路的最大数目。
5.二部图不含什么
算法题70分
1.用floyd定理求下列4x4的矩阵任意两点间的最短路径和距离
2.有五个游泳运动员X1,X2,X3,X4,X5,有五种游泳方式y1,y2,y3,y4,y5,请问怎么做才能在5x100混合泳接力赛上获得最好的成绩,下面给出这五名运动员的每种泳姿的成绩矩阵,为5x5矩阵。(用最大权值的匹配算法)
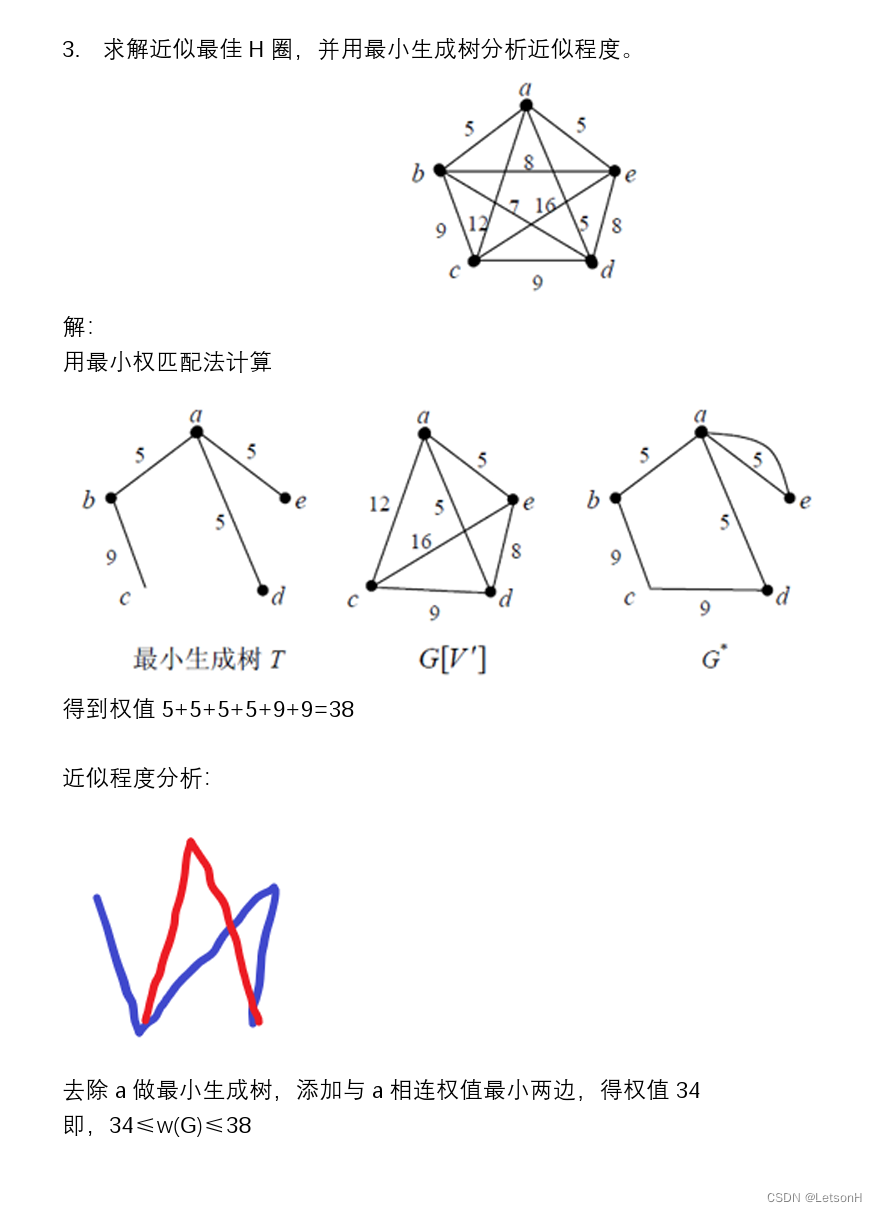
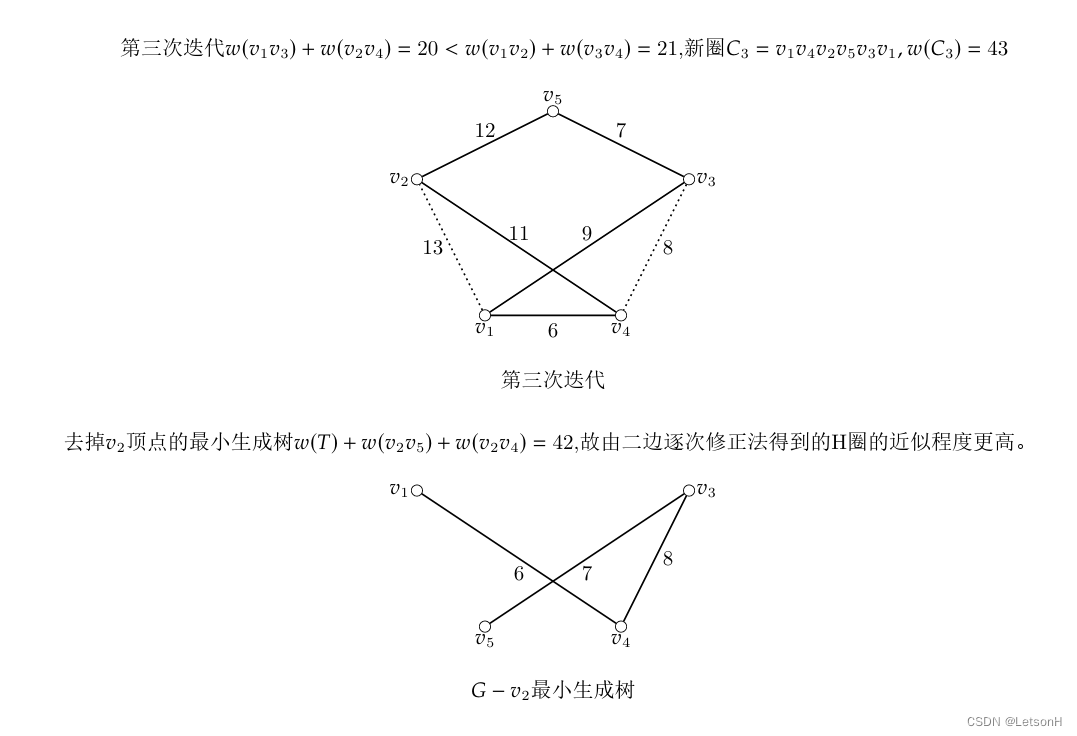
3.如下图,即图论P142的图6.39所示的图,求近似最佳H圈,并分析解的近似程度。
4.用可平面性算法证明彼得森图是非平面图。(彼得森图在P161图7.8所示)
证明题10分
1.证明对于简单图G,delta>=2,则有长至少为delta+1的圈
2.证明无向树是二部图