文章目录
- 求 n n n 的第 k k k 位是二进制的几
- lowbit(n)操作求解 n n n 的最后一个 1 1 1
- 题目练习
- AcWing 801. 二进制中1的个数
- CODE1
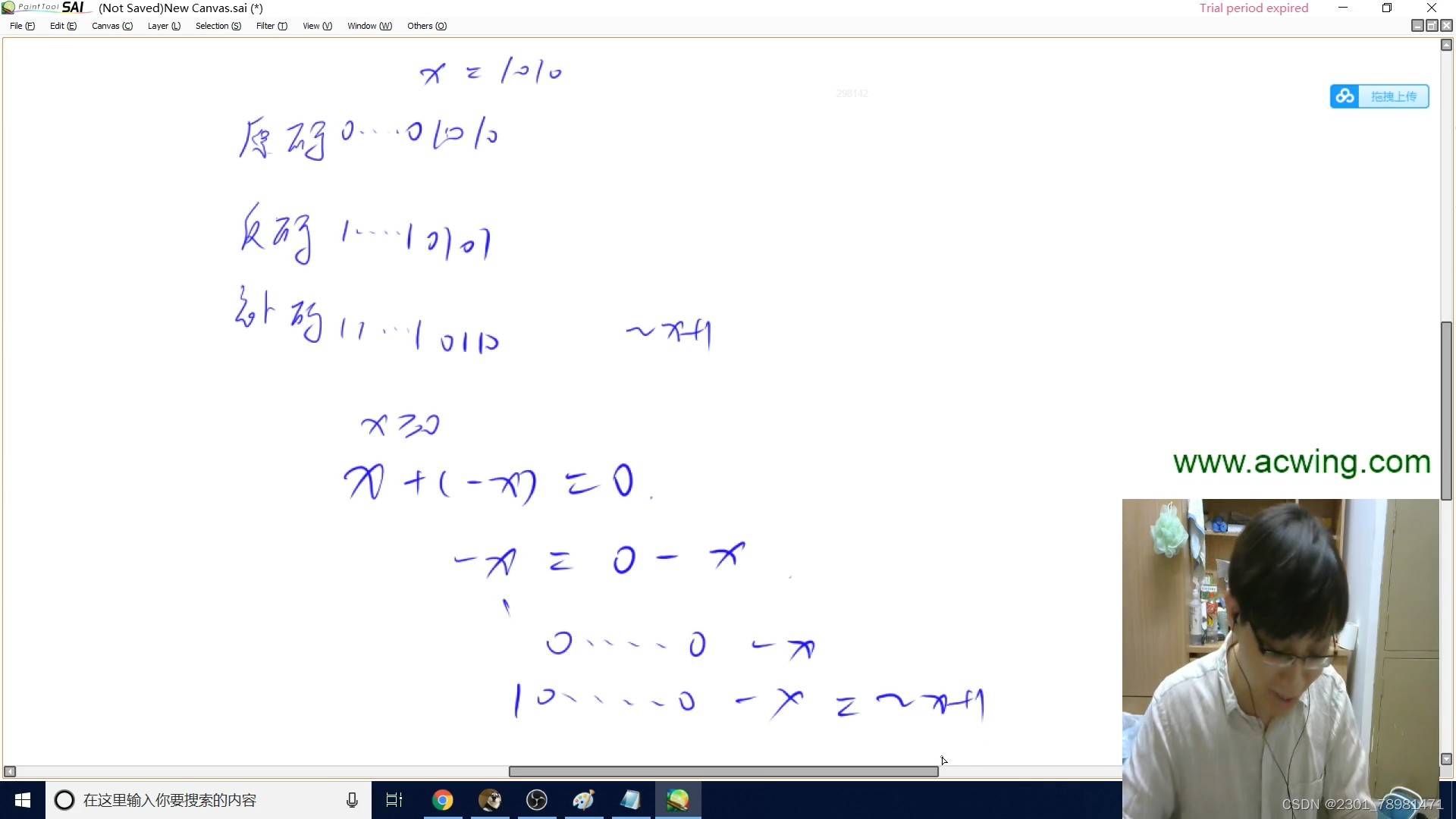
- 原码、补码、反码
-
求 n n n 的第 k k k 位是二进制的几
- 我们需要用到
&运算符:两位都为 1 1 1 时结果才为 1 1 1 ,否则为 0 0 0 - 公式: n > > k & 1 n >> k \& 1 n>>k&1
- 我们需要用到
-
lowbit(n)操作求解 n n n 的最后一个 1 1 1
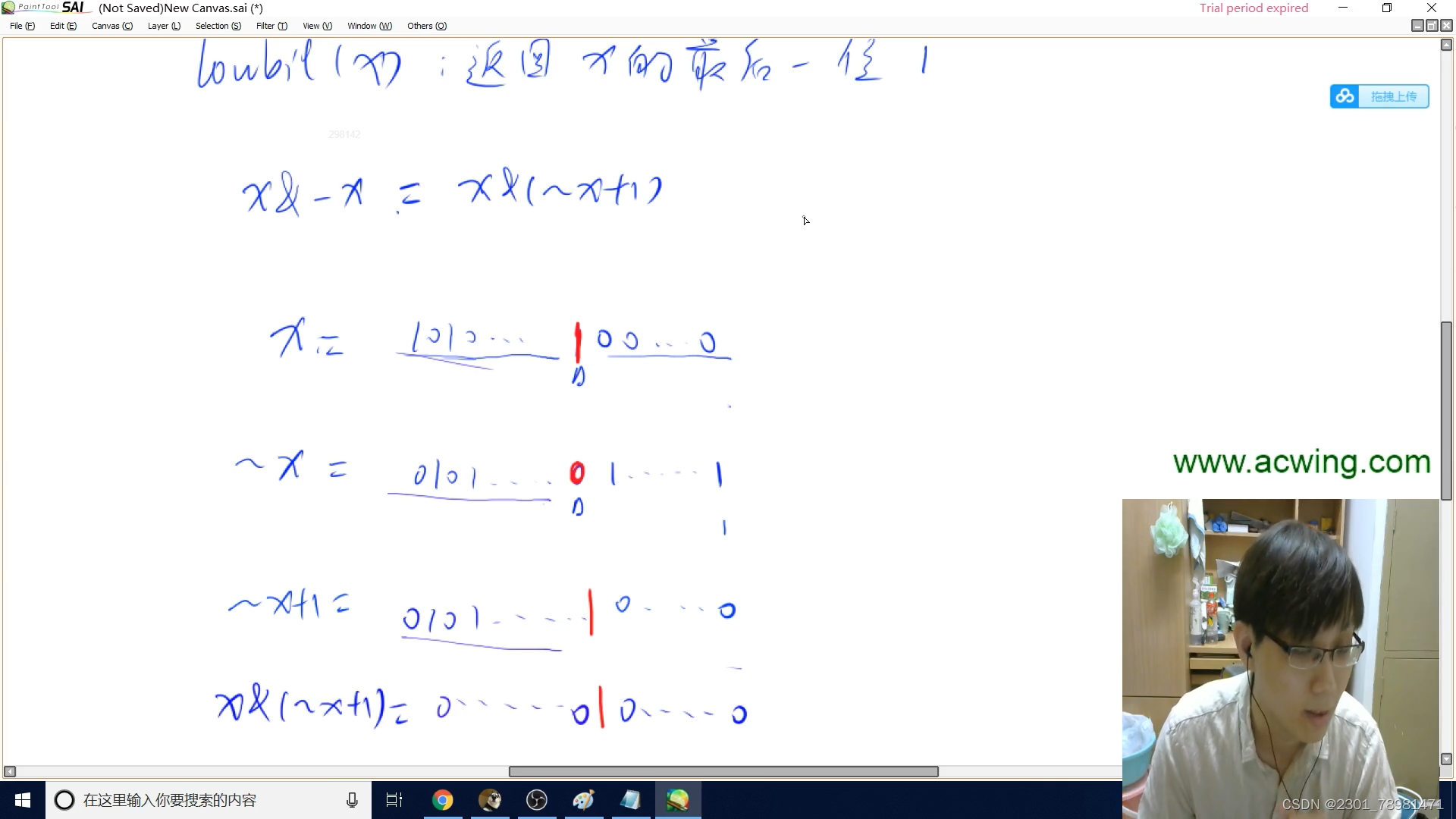
- 由此我们可以得到公式: l o w b i t ( x ) = x & ( − x ) lowbit(x) = x \& (-x) lowbit(x)=x&(−x) 最终得到一个 1 1 1 后面跟着一串 0 0 0
- 评论区dalao的方案


题目练习
AcWing 801. 二进制中1的个数
题目链接:https://www.acwing.com/problem/content/description/803/
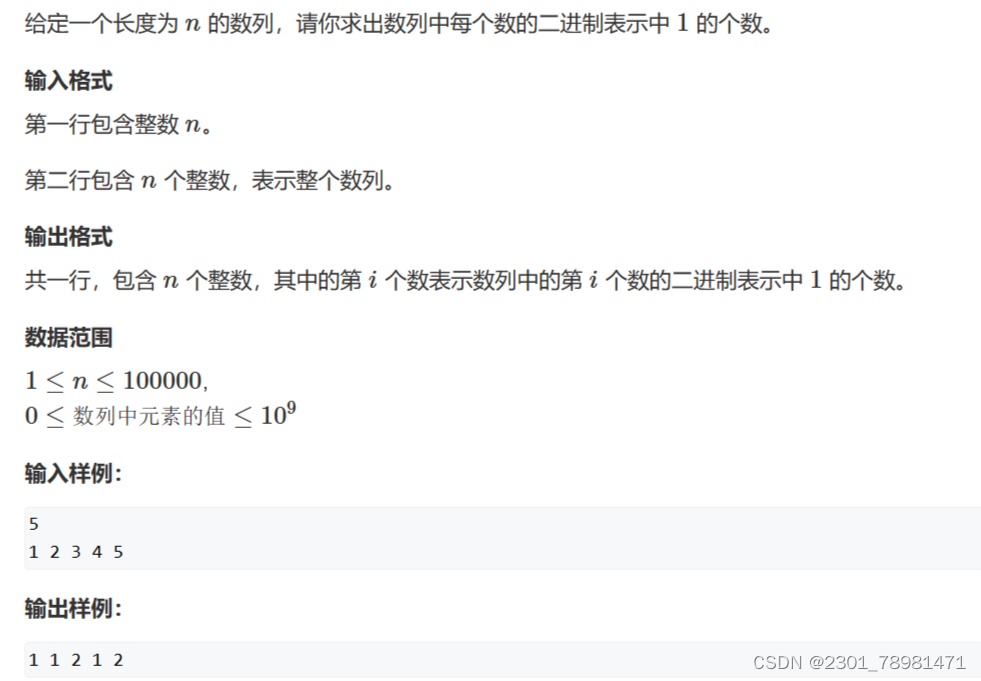
- 直接用我们刚刚的结论即可
CODE1
#include <queue> #include <iostream> #include <cstring> #include <algorithm> using namespace std; int n; int lowbit(int n){ return n & (-n); } int main() { cin >> n; while(n--){ int x, ans = 0; cin >> x; while(x) ans++, x -= lowbit(x); //只要x不为0,那就肯定含1 cout << ans << ' '; } }###CODE2
#include <queue> #include <iostream> #include <cstring> #include <algorithm> using namespace std; int n; int main() { cin >> n; while(n--){ int x, ans = 0; cin >> x; while(x) ans++, x &= x - 1; cout << ans << ' '; } }