系列文章目录
目录
系列文章目录
前言
一、分解问题
二、解决子问题
三、合并结果
总结
前言
刷题按照:
[力扣刷题攻略] Re:从零开始的力扣刷题生活 - 力扣(LeetCode)

参考:
「五大常用算法」一文搞懂分治算法 - 知乎 (zhihu.com)
分治算法(divide and conquer)是五大常用算法(分治算法、动态规划算法、贪心算法、回溯法、分治界限法)之一,分治,字面上的解释是“分而治之”,就是把一个复杂的问题分成两个或更多的相同或相似的子问题,再把子问题分成更小的子问题……直到最后子问题可以简单的直接求解,原问题的解即子问题的解的合并。在计算机科学中,分治法就是运用分治思想的一种很重要的算法。分治法是很多高效算法的基础,如排序算法(快速排序,归并排序),傅立叶变换(快速傅立叶变换)等等。
一、分解问题
169. 多数元素 - 力扣(LeetCode)

//方法一:排序取中值
// class Solution {
// public int majorityElement(int[] nums) {
// Arrays.sort(nums);
// return nums[nums.length/2];
// }
// }
//方法二:投票法,众数的个数大于n/2,顾投票总数大于0
// class Solution {
// public int majorityElement(int[] nums) {
// int count = 0;
// Integer mode = null;
// for(int num : nums)
// {
// if(count == 0)
// {
// mode = num;
// }
// count += (num == mode) ? 1 : -1;
// }
// return mode;
// }
// }
//方法三:HashMap,数组元素作为键值对的Key,出现个数作为键值对的Value,存放时出现相同的Key,将对应Value进行加1后放到
//HashMap中,遍历数据完成后返回Value值大于n/2的即可。
// class Solution {
// public int majorityElement(int[] nums) {
// Map<Integer, Integer> countMap = new HashMap<> ();
// for(int num : nums)
// {
// if(!countMap.containsKey(num))
// {
// countMap.put(num, 1);
// }
// else
// {
// countMap.put(num, countMap.get(num) + 1);
// }
// if(countMap.get(num) > nums.length / 2)
// {
// return num;
// }
// }
// return -1;
// }
// }
// //方法四:回调投票
class Solution {
public int majorityElement(int[] nums) {
return moore(0, nums, nums[0]);
}
public int moore(int i, int[] nums, int mode){
int count = 0;
for(int j = i; j < nums.length; j++){
if(nums[j] == mode){
count++;
}
else{
count--;
}
if(count < 0){
return moore(j, nums, nums[j]);
}
}
return mode;
}
}
4. 寻找两个正序数组的中位数 - 力扣(LeetCode)

class Solution {
public double findMedianSortedArrays(int[] nums1, int[] nums2) {
int totalLength = nums1.length + nums2.length;
int halfLength = totalLength / 2;
if (totalLength % 2 == 0) {
// 如果总长度是偶数,中位数是左侧部分的最大值和右侧部分的最小值之和的一半
double leftMedian = findKthElement(nums1, 0, nums2, 0, halfLength);
double rightMedian = findKthElement(nums1, 0, nums2, 0, halfLength + 1);
return (leftMedian + rightMedian) / 2.0;
} else {
// 如果总长度是奇数,中位数就是右侧部分的最小值
return findKthElement(nums1, 0, nums2, 0, halfLength + 1);
}
}
private double findKthElement(int[] nums1, int start1, int[] nums2, int start2, int k) {
if (start1 == nums1.length) {
// 如果 nums1 部分已经为空,则直接返回 nums2 部分的第 k 个元素
return nums2[start2 + k - 1];
}
if (start2 == nums2.length) {
// 如果 nums2 部分已经为空,则直接返回 nums1 部分的第 k 个元素
return nums1[start1 + k - 1];
}
if (k == 1) {
// 如果 k 等于 1,则直接返回两个数组当前部分的最小值
return Math.min(nums1[start1], nums2[start2]);
}
// 在两个数组中寻找第 k/2 个元素,并更新两个数组的起始位置
int mid1 = start1 + k / 2 - 1 < nums1.length ? nums1[start1 + k / 2 - 1] : Integer.MAX_VALUE;
int mid2 = start2 + k / 2 - 1 < nums2.length ? nums2[start2 + k / 2 - 1] : Integer.MAX_VALUE;
if (mid1 < mid2) {
// 如果 nums1 的中间元素小于 nums2 的中间元素,则舍弃 nums1 的左侧部分
return findKthElement(nums1, start1 + k / 2, nums2, start2, k - k / 2);
} else {
// 如果 nums1 的中间元素大于等于 nums2 的中间元素,则舍弃 nums2 的左侧部分
return findKthElement(nums1, start1, nums2, start2 + k / 2, k - k / 2);
}
}
}
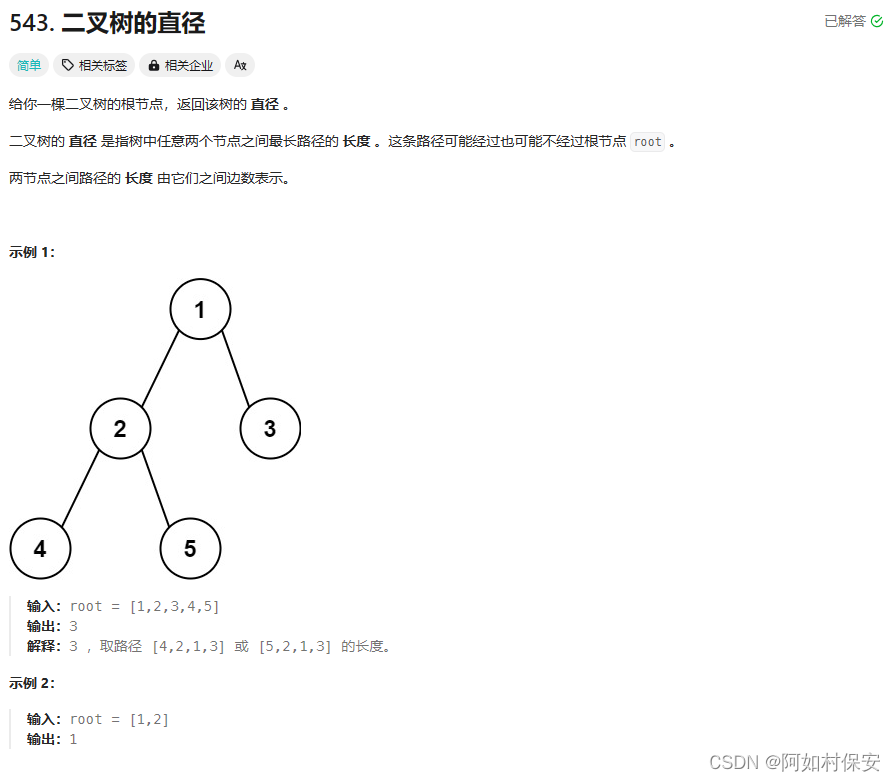
543. 二叉树的直径 - 力扣(LeetCode)

/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
int max = 0;
public int diameterOfBinaryTree(TreeNode root) {
if (root == null) {
return 0;
}
dfs(root);
return max;
}
private int dfs(TreeNode root) {
if (root.left == null && root.right == null) {
return 0;
}
int leftSize = root.left == null? 0: dfs(root.left) + 1;
int rightSize = root.right == null? 0: dfs(root.right) + 1;
max = Math.max(max, leftSize + rightSize);
return Math.max(leftSize, rightSize);
}
}
二、解决子问题
69. x 的平方根 - 力扣(LeetCode)

牛顿迭代法:Integer square root - Wikipedia

class Solution {
public int mySqrt(int x) {
if (x == 0) {
return 0;
}
double x0 = x; // 初始猜测值
double x1 = 0.5 * (x0 + x / x0); // 使用牛顿迭代法更新猜测值
// 迭代直到猜测值不再变化
while (Math.abs(x1 - x0) >= 1) {
x0 = x1;
x1 = 0.5 * (x0 + x / x0);
}
return (int) x1; // 将最终结果转换为整数并返回
}
}
一个特殊的方法来计算平方根,即通过取指数和对数的方式。实际上,这是一种常见的近似计算方法。它的基本思想是,计算 x 的平方根,可以转换为计算 e^(0.5 * ln(x))。在这里,Math.exp(0.5 * Math.log(x)) 计算的是 e^(0.5 * ln(x))。
class Solution {
public int mySqrt(int x) {
if (x == 0) {
return 0;
}
int ans = (int) Math.exp(0.5 * Math.log(x));
return (long) (ans + 1) * (ans + 1) <= x ? ans + 1 : ans;
}
}
53. 最大子数组和 - 力扣(LeetCode)

class Solution {
public int maxSubArray(int[] nums) {
int ans = Integer.MIN_VALUE;
int count = 0;
for (int i=0; i<nums.length; i++) {
count = Math.max(count + nums[i], nums[i]);
ans = Math.max(ans, count);
}
return ans;
}
}
34. 在排序数组中查找元素的第一个和最后一个位置 - 力扣(LeetCode)

class Solution {
public int[] searchRange(int[] nums, int target) {
int[] res = {-1, -1};
// 寻找第一个出现的位置
int left = 0, right = nums.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] == target) {
res[0] = mid;
right = mid - 1; // 继续在左半边搜索
} else if (nums[mid] < target) {
left = mid + 1;
} else {
right = mid - 1;
}
}
// 如果未找到目标值,直接返回
if (res[0] == -1) {
return res;
}
// 寻找最后一个出现的位置
left = res[0]; // 左边界从第一次找到的位置开始
right = nums.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] == target) {
res[1] = mid;
left = mid + 1; // 继续在右半边搜索
} else if (nums[mid] < target) {
left = mid + 1;
} else {
right = mid - 1;
}
}
return res;
}
}

三、合并结果
23. 合并 K 个升序链表 - 力扣(LeetCode)


/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
// 合并两个有序链表
public ListNode mergeKLists(ListNode[] lists) {
if (lists.length == 0) {
return null;
}
return split(lists, 0, lists.length - 1);
}
public ListNode split(ListNode[] lists, int i, int j) {
// System.out.println(i + " " + j);
if (j == i) {
return lists[i];
}
int m = (i + j) >>> 1;
return mergeTwoLists(
split(lists, i, m),
split(lists, m + 1, j)
);
}
public ListNode mergeTwoLists(ListNode p1, ListNode p2) {
if (p2 == null || p1 == null) {
return p2 == null ? p1 : p2;
}
if (p1.val < p2.val) {
p1.next = mergeTwoLists(p1.next, p2);
return p1;
} else {
p2.next = mergeTwoLists(p1, p2.next);
return p2;
}
}
}
1277. 统计全为 1 的正方形子矩阵 - 力扣(LeetCode)


动态规划
class Solution {
public int countSquares(int[][] matrix) {
// 动态规划, 二维数组dp[i][j]表示以i,j为右下角的最大的全1正方形的边长
// if matrix[i][j] == '1' -> dp[i][j] = Min{dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]} + 1
int m = matrix.length;
int n = matrix[0].length;
int[][] dp = new int[m][n];
// 初始化边界
int result = 0;
for (int i = 0; i < m; i++) {
if (matrix[i][0] == 1) {
dp[i][0] = 1;
}
}
for (int i = 0; i < n; i++) {
if (matrix[0][i] == 1) {
dp[0][i] = 1;
}
}
// 自底向上
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
if (matrix[i][j] == 0) {
dp[i][j] = 0;
} else {
dp[i][j] = Math.min(dp[i - 1][j - 1], Math.min(dp[i - 1][j], dp[i][j - 1])) + 1;
}
}
}
// 遍历dp
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
result += dp[i][j];
}
}
return result;
}
} 
总结
分治法很重要,然后我发现做题勾勾画画还挺有用的,希望多敲多做,慢慢来吧。


![[VNCTF 2023] web刷题记录](https://img-blog.csdnimg.cn/direct/4f549ab95bd44b5e92700a70b9c7142e.png)