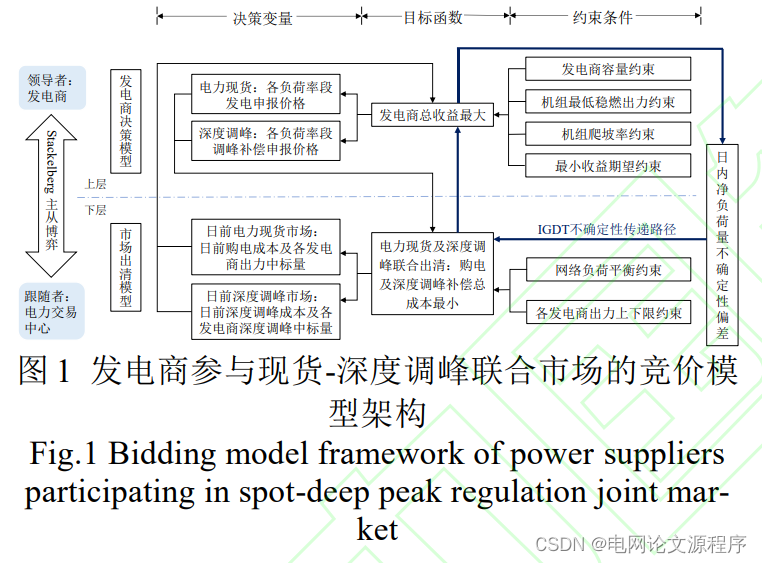
标题涉及到电力行业的领域,尤其是火电发电商在电力市场中面对深度调峰需求时的决策问题。下面是对标题的解读:
-
考虑不确定性: 这指的是在制定优化决策时,考虑到环境的不确定性,可能包括但不限于电力市场的价格波动、发电成本的变化、能源供应的不确定性等因素。在实际情况中,不确定性通常需要通过建模和分析来考虑。
-
火电发电商: 指的是以火力发电为主要方式的发电公司。火电是一种常见的发电方式,通常涉及燃煤、燃油等。
-
现货-深度调峰市场: 这可能涉及到电力市场的两个方面。首先,“现货市场”通常指的是电力市场中即期交易,即按照实际用电需求和供给情况进行的电力交易。其次,“深度调峰市场”则指的是在电力系统面临高峰需求时,采取深度调度和调峰措施,确保电力供需平衡。
-
优化决策: 在电力市场中,发电商需要通过优化决策来最大化其收益或者最小化成本。这可能涉及到合理配置发电资源,根据市场价格进行调整,以及考虑到环境和政策的不确定性来做出最佳的决策。
因此,整体来看,这个标题表明了一个复杂的电力市场环境中,火电发电商在深度调峰市场中面临的决策问题,并且考虑到不确定性的因素。可能需要运用一些优化算法、风险管理策略等方法来制定合理的决策方案。
摘要:针对电力现货市场与深度调峰市场联合运行背景下发电商电能量利润空间压缩、深度调峰功能亟待拓展等问题,发电商需通过确定最优日前竞价策略、合理分配参与现货及调峰市场的电量实现两市场总利润最大化。提出考虑不确定性的发电商现货-深度调峰市场优化策略。基于Stackelberg主从博弈,构建兼顾联合市场利润和风险的发电商日前报价策略双层优化模型:上层模型以发电商联合市场利润最大化为目标,对发电商分段报价进行优化;下层模型考虑竞争对手报价场景的不确定性,提出电力现货-深度调峰市场联合出清模型。针对净负荷不确定性,引入波动不确定度参数,将双层模型转换为基于信息间隙决策理论的发电商现货-深度调峰市场决策模型。基于安徽省实际市场数据进行仿真验证,得到适应不同负荷场景的发电商联合市场日前报价策略,结果表明考虑不确定性的联合优化决策能够有效规避负荷不确定性带来的利润波动风险。
这段摘要描述了针对电力市场中现货和深度调峰市场联合运行时,发电商面临的问题。这些问题包括电能量利润空间的压缩以及深度调峰功能亟待扩展等方面。为了应对这些挑战,发电商需要通过确定最优的日前竞价策略,并合理分配参与现货和调峰市场的电量,以实现两市场总利润的最大化。
为了解决这些问题,提出了考虑不确定性的发电商现货-深度调峰市场优化策略。使用Stackelberg主从博弈理论,构建了双层优化模型。上层模型旨在最大化发电商的联合市场利润,通过优化分段报价策略来实现这一目标。下层模型考虑了竞争对手报价场景的不确定性,并提出了电力现货-深度调峰市场的联合出清模型。
针对净负荷不确定性,引入了波动不确定度参数,将双层模型转换为基于信息间隙决策理论的发电商现货-深度调峰市场决策模型。使用安徽省的实际市场数据进行了仿真验证,并得出了适应不同负荷场景的发电商联合市场日前报价策略。结果表明,考虑不确定性的联合优化决策能够有效地规避负荷不确定性带来的利润波动风险。
关键词:现货深度调峰联合市场:发电商竞价策略; Stackelberg博弈; 不确定性:信息间隙决策理论;
-
现货深度调峰联合市场:
- 现货市场: 指电力市场中进行即期交易的市场,涉及按照实际用电需求和供给情况进行的电力交易。
- 深度调峰市场: 指在电力系统面临高峰需求时,通过深度调度和调峰措施确保电力供需平衡的市场。
-
发电商竞价策略:
- 描述发电商在市场中制定价格和销售电力的策略,这涉及到参与现货和深度调峰市场,以最大化其总体利润。
-
Stackelberg博弈:
- Stackelberg博弈理论: 一种博弈理论,指的是博弈中有一方(领导者)能够先行选择策略,而其他方(追随者)在了解领导者的选择后再进行策略选择。在这个上下游的关系中,领导者会优先选择最有利于自己的策略。
-
不确定性:
- 不确定性: 表示在决策和规划中存在的不可预测的因素,这可能包括市场波动、竞争对手行为、天气变化等。
-
信息间隙决策理论:
- 信息间隙决策理论: 一种决策理论,用于处理决策者对环境和他人信息的了解不完全的情况。在这个场景中,决策者通过填补信息缺口来做出决策,以最大程度地减少不确定性。
综合起来,关键词揭示了一个复杂的电力市场环境,其中发电商需要在现货和深度调峰市场中制定竞价策略。采用Stackelberg博弈理论,考虑了不确定性因素,并运用信息间隙决策理论来处理不完全信息的情况,以优化发电商的决策,最大程度地降低市场不确定性带来的风险。
仿真算例:以安徽省实际电力市场为例进行算例仿真。某典型日市场公布的预测发电情况如附录 A 图 A2所示。该省内用电实际负荷最小值为 1 640 MW,实际用电峰谷差为 960 MW。当天电网风电最大出力为 420 MW,中午风光叠加最大出力为 660 MW,净负荷最小值为 1 600 MW。有图可知,由于光伏出力的作用,净负荷最小值转移至中午时段,净负荷峰谷差为 600 MW,比原始用电负荷峰谷差增大66.7%。新能源消纳缺口增大,调峰利润空间扩张,发电商在联合市场中需协调深度调峰和现货市场中的决策,以获得最大综合利润。
系统参数:发电商 i 的容量为 500 MW,与发电商 i 有竞争关系的其他发电商的总发电容量为 2000 MW。根据目前部分省份的电力市场规定,发电商采用非递减报价原则,按机组负荷率分段报价。以机组负荷率 0.5 为分界:当机组负荷率高于 0.5 时,为现货报价区段;当机组负荷率低于 0.5 时,为深度调峰报价区段。发电商 i 的有关参数及市场报价规则分别如附录 A 表 A1、A2 所示。仿真通过 64 位Windows10 操作系统实现,在内存 16.0 GB、主频2.3 GHz 的 CPU 环境中完成运算,在 MATLABR2019b 编译环境下对所提理论模型进行求解。
仿真程序复现思路:
仿真的复现思路可以按照以下步骤进行,以MATLAB为例:
- 建立模型: 根据文中描述的电力市场模型,包括发电商的容量、竞争关系、报价原则等参数,以及市场预测数据,建立仿真模型。
% 定义系统参数
capacity_i = 500; % 发电商i容量
total_capacity_other = 2000; % 与发电商i有竞争关系的其他发电商总发电容量
% 定义报价原则
load_ratio_threshold = 0.5; % 机组负荷率分界
spot_price_zone = 'above'; % 现货报价区段
peak_price_zone = 'below'; % 深度调峰报价区段
% 读取市场预测数据
% (这里需要根据实际情况加载附录A中的图A2所示的市场预测数据)
% ... 还可以根据需要定义其他系统参数
- 编写算法: 根据论文中描述的算法,例如Stackelberg博弈、非递减报价原则等,编写相应的算法来模拟发电商的决策过程。
% 假设采用Stackelberg博弈模型
% ... 编写Stackelberg博弈算法的MATLAB代码
% 根据非递减报价原则生成报价曲线
% ... 编写报价曲线生成的MATLAB代码
% ... 还可以根据需要编写其他算法
- 运行仿真: 在MATLAB环境下,运行所编写的仿真代码,模拟电力市场中发电商的行为和市场的运作。
% 运行Stackelberg博弈算法
% ... 运行Stackelberg博弈算法的MATLAB代码
% 运行报价曲线生成算法
% ... 运行报价曲线生成的MATLAB代码
% ... 运行其他算法的代码
- 分析结果: 分析仿真结果,包括发电商的报价、市场清算情况、综合利润等。
% 分析仿真结果
% ... 编写分析仿真结果的MATLAB代码
% 输出仿真结果
% ... 输出分析结果,例如综合利润、报价曲线等
- 可视化结果: 如果有必要,可以使用MATLAB的绘图功能将仿真结果可视化,以便更直观地理解市场行为。
% 绘制仿真结果的图表
% ... 使用MATLAB的绘图函数绘制仿真结果的图表
请注意,上述代码仅为伪代码示例,具体的仿真实现需要根据文中提供的详细信息以及实际数据进行进一步的细化和完善。