人工智能-优化算法之梯度下降

news2024/11/26 7:36:10

梯度下降

尽管梯度下降（gradient descent）很少直接用于深度学习，但了解它是理解下一节随机梯度下降算法的关键。例如，由于学习率过大，优化问题可能会发散，这种现象早已在梯度下降中出现。同样地，预处理（preconditioning）是梯度下降中的一种常用技术，还被沿用到更高级的算法中。让我们从简单的一维梯度下降开始。

下面我们来展示如何实现梯度下降。为了简单起见，我们选用目标函数 $f(x)=x^{2}$ 。尽管我们知道 $x=0$ 时 $f(x)$ 能取得最小值，但我们仍然使用这个简单的函数来观察 $(x)$ 的变化。

%matplotlib inline
from mxnet import np, npx
from d2l import mxnet as d2l

npx.set_np()

def f(x):  # 目标函数
    return x ** 2

def f_grad(x):  # 目标函数的梯度(导数)
    return 2 * x

%matplotlib inline
import numpy as np
import torch
from d2l import torch as d2l

def f(x):  # 目标函数
    return x ** 2

def f_grad(x):  # 目标函数的梯度(导数)
    return 2 * x

%matplotlib inline
import numpy as np
import tensorflow as tf
from d2l import tensorflow as d2l

def f(x):  # 目标函数
    return x ** 2

def f_grad(x):  # 目标函数的梯度(导数)
    return 2 * x

%matplotlib inline
import warnings
from d2l import paddle as d2l

warnings.filterwarnings("ignore")
import numpy as np
import paddle

def f(x):  # 目标函数
    return x ** 2

def f_grad(x):  # 目标函数的梯度(导数)
    return 2 * x

接下来，我们使用 $x=10$ 作为初始值，并假设 $eta=0.2$ 。使用梯度下降法迭代$x$共10次，我们可以看到， $(x)$ 的值最终将接近最优解。

def gd(eta, f_grad):
    x = 10.0
    results = [x]
    for i in range(10):
        x -= eta * f_grad(x)
        results.append(float(x))
    print(f'epoch 10, x: {x:f}')
    return results

results = gd(0.2, f_grad)

epoch 10, x: 0.060466

def gd(eta, f_grad):
    x = 10.0
    results = [x]
    for i in range(10):
        x -= eta * f_grad(x)
        results.append(float(x))
    print(f'epoch 10, x: {x:f}')
    return results

results = gd(0.2, f_grad)

epoch 10, x: 0.060466

def gd(eta, f_grad):
    x = 10.0
    results = [x]
    for i in range(10):
        x -= eta * f_grad(x)
        results.append(float(x))
    print(f'epoch 10, x: {x:f}')
    return results

results = gd(0.2, f_grad)

epoch 10, x: 0.060466

def gd(eta, f_grad):
    x = 10.0
    results = [x]
    for i in range(10):
        x -= eta * f_grad(x)
        results.append(float(x))
    print(f'epoch 10, x: {float(x):f}')
    return results

results = gd(0.2, f_grad)

epoch 10, x: 0.060466

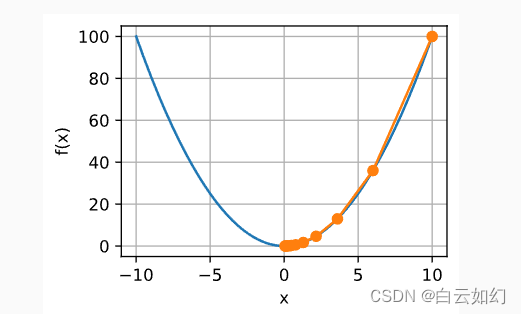
对进行 $x$ 优化的过程可以绘制如下：

def show_trace(results, f):
    n = max(abs(min(results)), abs(max(results)))
    f_line = np.arange(-n, n, 0.01)
    d2l.set_figsize()
    d2l.plot([f_line, results], [[f(x) for x in f_line], [
        f(x) for x in results]], 'x', 'f(x)', fmts=['-', '-o'])

show_trace(results, f)

[07:12:32] ../src/storage/storage.cc:196: Using Pooled (Naive) StorageManager for CPU

def show_trace(results, f):
    n = max(abs(min(results)), abs(max(results)))
    f_line = torch.arange(-n, n, 0.01)
    d2l.set_figsize()
    d2l.plot([f_line, results], [[f(x) for x in f_line], [
        f(x) for x in results]], 'x', 'f(x)', fmts=['-', '-o'])

show_trace(results, f)

def show_trace(results, f):
    n = max(abs(min(results)), abs(max(results)))
    f_line = tf.range(-n, n, 0.01)
    d2l.set_figsize()
    d2l.plot([f_line, results], [[f(x) for x in f_line], [
        f(x) for x in results]], 'x', 'f(x)', fmts=['-', '-o'])

show_trace(results, f)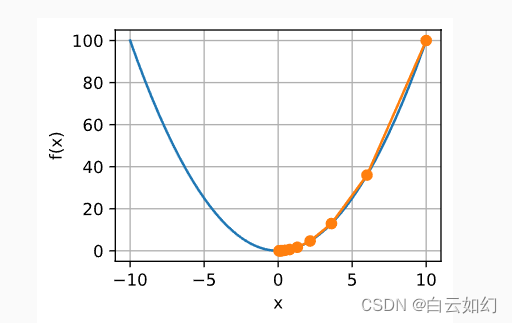

def show_trace(results, f):
    n = max(abs(min(results)), abs(max(results)))
    f_line = paddle.arange(-n, n, 0.01, dtype='float32')
    d2l.set_figsize()
    d2l.plot([f_line, results], [[f(x) for x in f_line], [
        f(x) for x in results]], 'x', 'f(x)', fmts=['-', '-o'])

show_trace(results, f)