基本原理

AffinityPropagation按照字面意思就是亲和力传播，可见这个算法的关键就是亲和力与传播。

说到传播，无外乎两件事，第一件事，传的是什么，暂且先不用管，因为名字里已经说了，传的是亲和度；第二件事，怎么传，为了解决这个问题，就必须造一条传递亲和力的通道。

最直接的想法就是连接样本中所有的点，这样点与点之间就有了关联。
从而得到一个图。

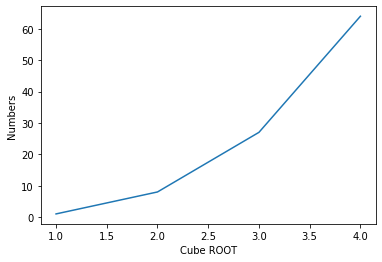
下面新建100个随机点，然后建立这100个随机点之间的距离矩阵，最后把距离矩阵画出来

import numpy as np
import matplotlib.pyplot as plt

from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs

X, y = make_blobs(100, centers=[(1,1),(11,11)])
ds = np.linalg.norm(X.reshape(-1,1,2)-X.reshape(1,-1,2), axis=2)

得到结果如图所示

其中绿色的值比较小，而蓝色比较大。值越小，意味着距离越短，也就是说更应该属于相同的类别，换言之，也就是越相似。在AP算法中，用负距离表示相似度，从而相似度越大则距离越短，则越相似。

相应地，距离矩阵取个负号，就是相似度矩阵了，其元素表示为

$$s_{ij}=-\Vert x_i-x_j{\Vert }^2$$

下面再详细地想一想这个亲和力到底是个啥，如果一个人很有亲和力的话，那么必然会吸引到其他人；反过来讲，只有这个人能够吸引到足够多的人，才说明这个人有亲和力，换言之，这个人需要依赖那些被他吸引的人。所以，AP算法通过相似度矩阵传递的真正内容，就是吸引和依赖。

吸引度$r_{ik}$由聚类中心$i$传给点$k$，用于累积$k$的竞争力；依赖度$a_{ik}$与之相反，表示在数据点$k$的帮助下，$i$才能成为聚类中心。

二者的更新方式如下

r i k = s i k − arg max ⁡ k ′ , k ′ ≠ k a i k ′ + s i k ′ a i k = min ⁡ ( 0 , r k k + ∑ i ′ , i ′ ∉ { i , k } max ⁡ ( 0 , r i ′ k ) ) \begin{aligned} r_{ik}&=s_{ik}-\argmax_{k', k'\not=k} a_{ik'}+s_{ik'}\\ a_{ik}&=\min(0, r_{kk}+\sum_{i', i'\not\in\{i,k\}}\max(0,r_{i'k})) \end{aligned} rik​aik​​=sik​−k′,k′=kargmax​aik′​+sik′​=min(0,rkk​+i′,i′∈{i,k}∑​max(0,ri′k​))​

其中$r_{kk}$为自吸引度，当该值为负数时，说明这个点不适合做聚类中心。随着不断迭代，如果一个聚类中心不适合做中心，那么其依赖度将会越来越小，最后顺利被聚类中心除名。

为了让迭代过程不那么剧烈，一般会在参数更新时添加一个阻尼系数$\lambda$，以吸引度为例，在得到第$t$代$r$之后，会考虑上一代$r$的影响，从而减小$t$更新的幅度。

$$r_t=(1-\lambda )r_t+\lambda r_{t-1}$$

sklearn中的实现

在sklearn中，AffinityPropagation类的阻尼系数为参数damping，其取值范围从0.5到1，取值越大，则迭代越快，默认为0.5。下面做一个最简单的示范，需要注意的是，AP算法效率很低，测试数据不宜过大。

from sklearn.cluster import AffinityPropagation as AP
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
import numpy as np
import time
from itertools import cycle

ys, xs = np.indices([2,2])*6
cens = list(zip(xs.reshape(-1), ys.reshape(-1)))
X, _ = make_blobs(1400, centers=cens)
y = AP(random_state=0).fit(X)
ccIndices = y.cluster_centers_indices_  # 质心坐标

colors = 'bgrcmykbgrcmykbgrcmykbgrcmyk'
for x,k in zip(X, y.labels_):
    cen = X[ccIndices[k]]
    plt.plot([cen[0], x[0]], [cen[1], x[1]], colors[k])

plt.show()

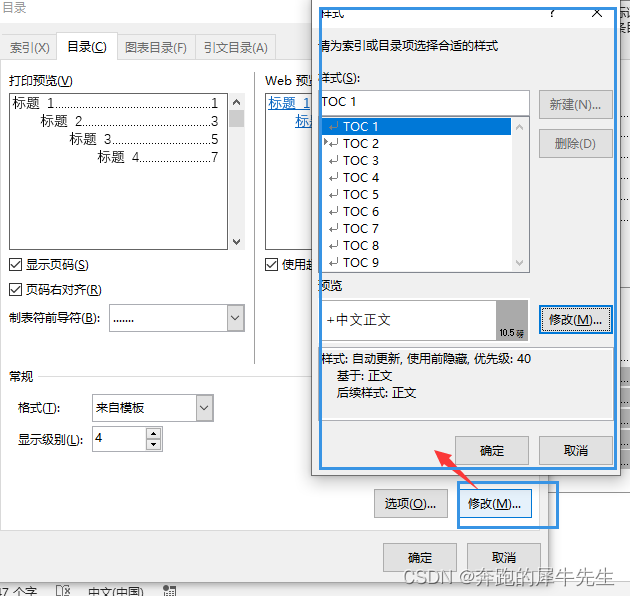
得到聚类结果