D - Sum of Large Numbers

不考虑$10^{100}$的情况下，检查能取到的最大和与最小和，此时中间的所有数都能取到
给出$10^{100}$的用意在于，确保取2个数与取3个数下面取到的和是不相同的。因此遍历取数的个数，累计答案。

# -*- coding: utf-8 -*-
# @time     : 2023/6/2 13:30
# @file     : atcoder.py
# @software : PyCharm

import bisect
import copy
import sys
from itertools import permutations
from sortedcontainers import SortedList
from collections import defaultdict, Counter, deque
from functools import lru_cache, cmp_to_key
import heapq
import math
sys.setrecursionlimit(1000)


def main():
    items = sys.version.split()
    if items[0] == '3.10.6':
        fp = open("in.txt")
    else:
        fp = sys.stdin

    n, k = map(int, fp.readline().split())
    ans = 0
    mod = 10 ** 9 + 7
    for i in range(k, n + 2):
        a = (0 + i - 1) * i // 2
        b = (n - i + 1 + n) * i // 2
        ans = (ans + (b - a + 1)) % mod
    print(ans)


if __name__ == "__main__":
    main()

E - Active Infants

区间dp
设$dp[i][j]$的区间为$l$，代表$\mathrm{1..}l$的数放入从i到j的位置能获得的最大数
从小往大放，最大的数应该放在两侧
$$dp(i,j)=max(dp(i+1,j)+cost(i),dp(i,j-1)+cost(j))$$

# -*- coding: utf-8 -*-
# @time     : 2023/6/2 13:30
# @author   : cd@zju.edu.cn
# @desc     :
# @file     : main.py
# @software : PyCharm

import bisect
import copy
import sys
from itertools import permutations
from collections import defaultdict, Counter, deque
from functools import lru_cache, cmp_to_key
import heapq
import math
sys.setrecursionlimit(50050)


def main():
    items = sys.version.split()
    if items[0] == '3.8.10':
        fp = open("in.txt")
    else:
        fp = sys.stdin
    n = int(fp.readline())
    a = list(map(int, fp.readline().split()))
    dp = [[0] * n for _ in range(n)]
    items = []
    for i, x in enumerate(a):
        items.append([x, i])
    items.sort()
    for i in range(n):
        dp[i][i] = items[0][0] * abs(items[0][1] - i)
    for l in range(2, n + 1):
        for i in range(n):
            j = i + l - 1
            if j >= n:
                break
            x, p = items[l - 1]
            dp[i][j] = max(dp[i + 1][j] + x * abs(p - i), dp[i][j - 1] + x * abs(p - j))
    ans = dp[0][n - 1]
    print(ans)


if __name__ == "__main__":
    main()

F - path pass i

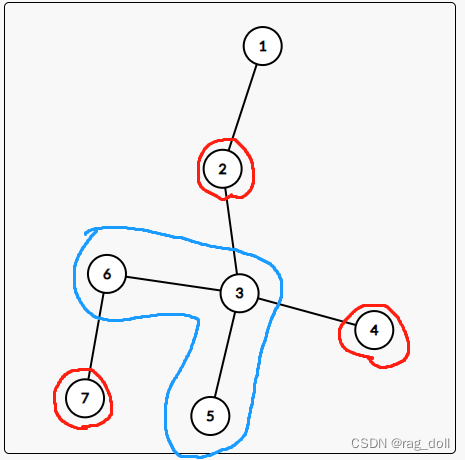
首先要反过来求没有颜色的点对，可以转换为求不同染色下的连通集。
本题的关键是建立sum数组，从而求出连通集的大小。
sum[i]数组按搜索顺序，意思为访问到当前，颜色为i的最大子树和
以上图为例，访问到2完成后，红色最大的子树是以2为节点，sum=6
而当访问3时，红色子树分为两颗：4与7，sum=2
在dfs处理时，设当前的节点为u，不能简单的将sz[u]加到sum中，而需要预先记录下之前的sum值
建立起sum数组后，按照u节点的子节点进行计算
如遍历到u=2后，枚举子节点3，发现子节点里面最大子树和为2，还剩下sz[v]-2=3。3就是连通集的大小，计入答案中。
最后别忘了将根节点所属连通集计入答案。

# -*- coding: utf-8 -*-
# @time     : 2023/6/2 13:30
# @file     : atcoder.py
# @software : PyCharm

import bisect
import copy
import sys
from itertools import permutations
from sortedcontainers import SortedList
from collections import defaultdict, Counter, deque
from functools import lru_cache, cmp_to_key
import heapq
import math
sys.setrecursionlimit(200020)


def main():
    items = sys.version.split()
    if items[0] == '3.10.6':
        fp = open("in.txt")
    else:
        fp = sys.stdin

    def f(x):
        return x * (x + 1) // 2

    n = int(fp.readline())
    ans = [f(n)] * (n + 1)
    sz = [0] * (n + 1)
    c = list(map(int, fp.readline().split()))
    c = [-1] + c
    s = [0] * (n + 1)
    g = [[] for _ in range(n + 1)]
    for i in range(n - 1):
        a, b = map(int, fp.readline().split())
        g[a].append(b)
        g[b].append(a)

    def dfs(u, fa):
        sz[u] = 1
        col = c[u]
        save = s[col]
        for v in g[u]:
            if v == fa:
                continue
            t = s[col]
            dfs(v, u)
            sz[u] += sz[v]
            dt = s[col] - t
            # print(v, col, s[col], t, sz[v] - dt)
            ans[col] -= f(sz[v] - dt)
        s[col] = save + sz[u]
        # 因为有包含关系，s[col]是当前访问到的根节点为col的最大的子树和
        # print(u, col, s[col])

    dfs(1, 0)
    for i in range(1, n + 1):
        ans[i] -= f(n - s[i])
        print(ans[i])


if __name__ == "__main__":
    main()