强化学习Q-Learning算法和简单迷宫代码

使用到的符号：

agent 代理
reward 奖励
state(s) 状态
action(a) 行为
R reward 矩阵
Q 矩阵：表示从经验中学到的知识
episode：表示初始→目标一整个流程

贝尔曼方程（迭代公式）：

$\leftarrow Q(s,a) + \alpha [R(s,a) + \gamma \mathop {\max }\limits_{a'} Q(s',a') - Q(s,a)]$

当 $\alpha = 1$ ：

$\leftarrow R(s,a) + \gamma \mathop {\max }\limits_{a'} Q(s',a')$

其中， $\alpha$ 是学习率， $\gamma$ 是超参数， $Q (s^{'}, a^{'})$ 表示下一个状态和行为。

以一个简单迷宫为例：设 agent 在房子内任意一个房间（0-4），迷宫出口为 5，即走出迷宫的条件是到房子外。
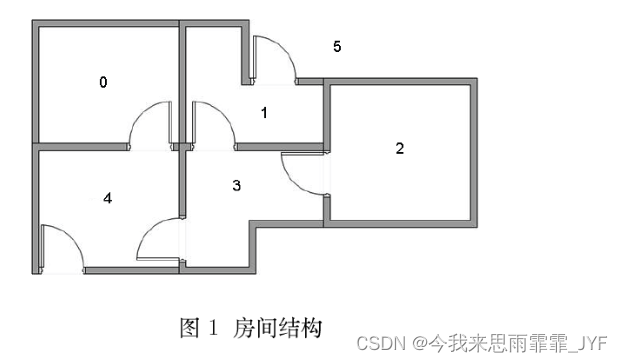
在这里插入图片描述
建模成图（“状态”对应节点，“行为”对应边）：

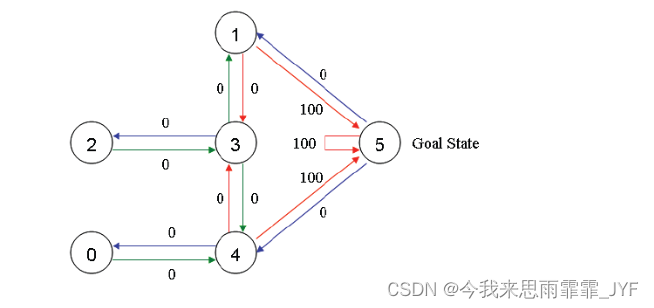
构建 R 矩阵（R 固定不变）：

初始化 Q 为零矩阵， $\gamma = 0.8$ ，以一个 episode 具体说明。

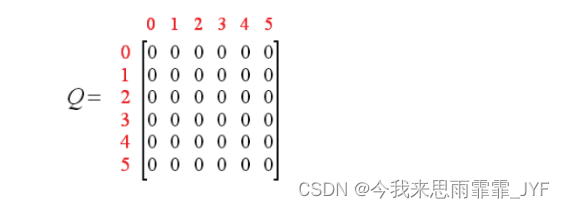
在这里插入图片描述

假设初始状态为 2。

① 当前状态 2 的下一步行为只能选 3，根据迭代公式，考虑下一个状态和行为，状态 3 可能的行为：1、2 或 4。

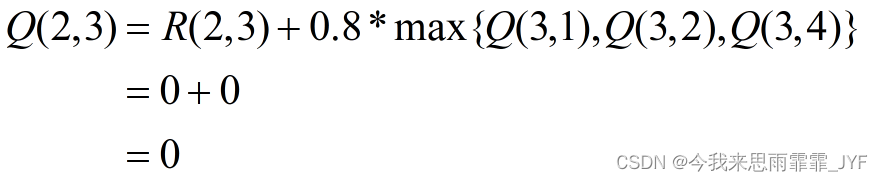
在这里插入图片描述
② 当前状态为 3，随机地，选取转至状态 4。下一个状态和行为：状态 4 可能的行为：0、3、5。

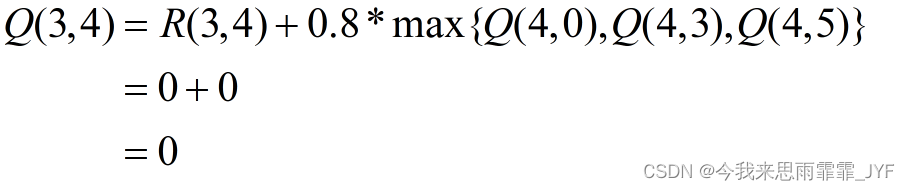
在这里插入图片描述
③ 当前状态为 4，随机地，选取转至状态 5。下一个状态和行为：状态 5 可能的行为：1、4、5。

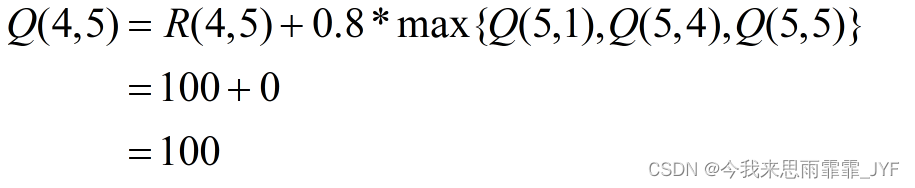
在这里插入图片描述

状态 5 为目标状态，故一次 episode 完成。

一次 episode 后的 Q 矩阵：

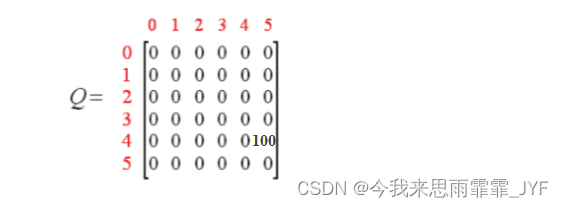
在这里插入图片描述

具体 Q-Learning 算法的计算步骤：

在这里插入图片描述

迷宫实例及代码：

红色方块是 agent ，黄色圆圈和黑色方块都是目标状态，其中，黄色圆圈的奖励为 1，黑色方块的奖励为 -1。该迷宫一共有 16 个状态，每个状态可能的行为：u（上），d（下），l（左），r（右）。

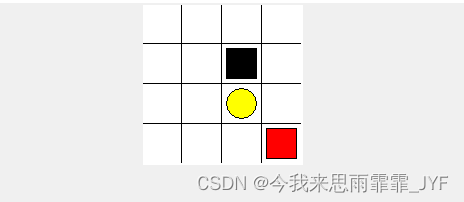
在这里插入图片描述

程序主循环

from Q_Learning.maze_env import Maze
from Q_Learning.RL_brain import DQN
import time


def run_maze():
    print("====Game Start====")
    step = 0
    max_episode = 500
    for episode in range(max_episode):
        state = env.reset()  # 重置智能体位置
        step_every_episode = 0
        epsilon = episode / max_episode  # 动态变化随机值
        while True:
            if episode < 10:
                time.sleep(0.001)
            if episode > 480:
                time.sleep(0.002)
            env.render()  # 显示新位置
            action = model.choose_action(state, epsilon)  # 根据状态选择行为
            # 环境根据行为给出下一个状态，奖励，是否结束。
            next_state, reward, terminal = env.step(action)
            model.store_transition(state, action, reward, next_state)  # 模型存储经历
            # 控制学习起始时间(先积累记忆再学习)和控制学习的频率(积累多少步经验学习一次)
            if step > 200 and step % 5 == 0:
                model.learn()
            # 进入下一步
            state = next_state
            if terminal:
                print("episode=", episode, end=",")
                print("step=", step_every_episode)
                break
            step += 1
            step_every_episode += 1
    # 游戏环境结束
    print("====Game Over====")
    env.destroy()


if __name__ == "__main__":
    env = Maze()  # 环境
    model = DQN(
        n_states=env.n_states,
        n_actions=env.n_actions
    )  # 算法模型
    run_maze()
    env.mainloop()
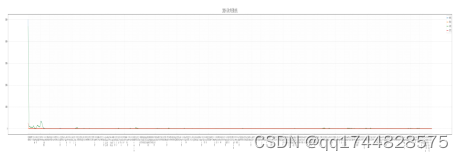
    model.plot_cost()  # 误差曲线

环境模块 maze_env.py

import tkinter as tk
import sys
import numpy as np

UNIT = 40  # pixels
MAZE_H = 4  # grid height
MAZE_W = 4  # grid width


class Maze(tk.Tk, object):
    def __init__(self):
        print("<env init>")
        super(Maze, self).__init__()
        # 动作空间(定义智能体可选的行为),action=0-3
        self.action_space = ['u', 'd', 'l', 'r']
        # 使用变量
        self.n_actions = len(self.action_space)
        self.n_states = 2
        # 配置信息
        self.title('maze')
        self.geometry("160x160")
        # 初始化操作
        self.__build_maze()

    def render(self):
        # time.sleep(0.1)
        self.update()

    def reset(self):
        # 智能体回到初始位置
        # time.sleep(0.1)
        self.update()
        self.canvas.delete(self.rect)
        origin = np.array([20, 20])
        self.rect = self.canvas.create_rectangle(
            origin[0] - 15, origin[1] - 15,
            origin[0] + 15, origin[1] + 15,
            fill='red')
        # return observation
        return (np.array(self.canvas.coords(self.rect)[:2]) - np.array(self.canvas.coords(self.oval)[:2])) / (MAZE_H * UNIT)

    def step(self, action):
        # 智能体向前移动一步：返回next_state,reward,terminal
        s = self.canvas.coords(self.rect)
        base_action = np.array([0, 0])
        if action == 0:  # up
            if s[1] > UNIT:
                base_action[1] -= UNIT
        elif action == 1:  # down
            if s[1] < (MAZE_H - 1) * UNIT:
                base_action[1] += UNIT
        elif action == 2:  # right
            if s[0] < (MAZE_W - 1) * UNIT:
                base_action[0] += UNIT
        elif action == 3:  # left
            if s[0] > UNIT:
                base_action[0] -= UNIT

        self.canvas.move(self.rect, base_action[0], base_action[1])  # move agent

        next_coords = self.canvas.coords(self.rect)  # next state

        # reward function
        if next_coords == self.canvas.coords(self.oval):
            reward = 1
            print("victory")
            done = True
        elif next_coords in [self.canvas.coords(self.hell1)]:
            reward = -1
            print("defeat")
            done = True
        else:
            reward = 0
            done = False
        s_ = (np.array(next_coords[:2]) - np.array(self.canvas.coords(self.oval)[:2])) / (MAZE_H * UNIT)
        return s_, reward, done

    def __build_maze(self):
        self.canvas = tk.Canvas(self, bg='white',
                                height=MAZE_H * UNIT,
                                width=MAZE_W * UNIT)

        # create grids
        for c in range(0, MAZE_W * UNIT, UNIT):
            x0, y0, x1, y1 = c, 0, c, MAZE_H * UNIT
            self.canvas.create_line(x0, y0, x1, y1)
        for r in range(0, MAZE_H * UNIT, UNIT):
            x0, y0, x1, y1 = 0, r, MAZE_W * UNIT, r
            self.canvas.create_line(x0, y0, x1, y1)
        origin = np.array([20, 20])
        hell1_center = origin + np.array([UNIT * 2, UNIT])
        self.hell1 = self.canvas.create_rectangle(
            hell1_center[0] - 15, hell1_center[1] - 15,
            hell1_center[0] + 15, hell1_center[1] + 15,
            fill='black')
        oval_center = origin + UNIT * 2
        self.oval = self.canvas.create_oval(
            oval_center[0] - 15, oval_center[1] - 15,
            oval_center[0] + 15, oval_center[1] + 15,
            fill='yellow')
        self.rect = self.canvas.create_rectangle(
            origin[0] - 15, origin[1] - 15,
            origin[0] + 15, origin[1] + 15,
            fill='red')
        self.canvas.pack()

DQN模型 RL_brain.py

import numpy as np
import torch
import torch.nn.functional as F
from torch import nn
import matplotlib.pyplot as plt


class Net(nn.Module):
    def __init__(self, n_states, n_actions):
        super(Net, self).__init__()
        self.fc1 = nn.Linear(n_states, 10)
        self.fc2 = nn.Linear(10, n_actions)
        self.fc1.weight.data.normal_(0, 0.1)
        self.fc2.weight.data.normal_(0, 0.1)

    def forward(self, x):
        x = self.fc1(x)
        x = F.relu(x)
        out = self.fc2(x)
        return out


class DQN:
    def __init__(self, n_states, n_actions):
        print("<DQN init>")
        # DQN有两个net:target net和eval net,具有选动作，存经历，学习三个基本功能
        self.eval_net, self.target_net = Net(n_states, n_actions), Net(n_states, n_actions)
        self.loss = nn.MSELoss()
        self.optimizer = torch.optim.Adam(self.eval_net.parameters(), lr=0.01)
        self.n_actions = n_actions
        self.n_states = n_states
        # 使用变量
        self.learn_step_counter = 0  # target网络学习计数
        self.memory_counter = 0  # 记忆计数
        self.memory = np.zeros((2000, 2 * 2 + 2))  # 2*2(state和next_state,每个x,y坐标确定)+2(action和reward),存储2000个记忆体
        self.cost = []  # 记录损失值

    def choose_action(self, x, epsilon):
        # print("<choose_action>")
        x = torch.unsqueeze(torch.FloatTensor(x), 0)  # (1,2)
        if np.random.uniform() < epsilon:
            action_value = self.eval_net.forward(x)
            action = torch.max(action_value, 1)[1].data.numpy()[0]
        else:
            action = np.random.randint(0, self.n_actions)
        # print("action=", action)
        return action

    def store_transition(self, state, action, reward, next_state):
        # print("<store_transition>")
        transition = np.hstack((state, [action, reward], next_state))
        index = self.memory_counter % 200  # 满了就覆盖旧的
        self.memory[index, :] = transition
        self.memory_counter += 1

    def learn(self):
        # print("<learn>")
        # target net 更新频率,用于预测，不会及时更新参数
        if self.learn_step_counter % 100 == 0:
            self.target_net.load_state_dict((self.eval_net.state_dict()))
        self.learn_step_counter += 1

        # 使用记忆库中批量数据
        sample_index = np.random.choice(200, 16)  # 2000个中随机抽取32个作为batch_size
        memory = self.memory[sample_index, :]  # 抽取的记忆单元，并逐个提取
        state = torch.FloatTensor(memory[:, :2])
        action = torch.LongTensor(memory[:, 2:3])
        reward = torch.LongTensor(memory[:, 3:4])
        next_state = torch.FloatTensor(memory[:, 4:6])

        # 计算loss,q_eval:所采取动作的预测value,q_target:所采取动作的实际value
        q_eval = self.eval_net(state).gather(1, action) # eval_net->(64,4)->按照action索引提取出q_value
        q_next = self.target_net(next_state).detach()
        # torch.max->[values=[],indices=[]] max(1)[0]->values=[]
        q_target = reward + 0.9 * q_next.max(1)[0].unsqueeze(1) # label
        loss = self.loss(q_eval, q_target)
        self.cost.append(loss)
        # 反向传播更新
        self.optimizer.zero_grad()  # 梯度重置
        loss.backward()  # 反向求导
        self.optimizer.step()  # 更新模型参数

    def plot_cost(self):
        plt.plot(np.arange(len(self.cost)), self.cost)
        plt.xlabel("step")
        plt.ylabel("cost")
        plt.show()

代码存在的一点缺陷：存在个别 episode 需要经过大量状态才能找到目标状态（主要表现在程序在两个状态间来回跳动：7→8→7→8→7→8…，需要很长时间才能跳出这个局限）

致谢：https://blog.csdn.net/itplus/article/details/9361915
https://www.cnblogs.com/nrocky/p/14496252.html