多项式

我们从课本中可以知道，一个 $n-1$ 次的多项式可以写成 $a_0+a_{1}x+a_2{x}^2+a_3{x}^3+\cdots +a_{n-1}{x}^{n-1}$

用高级一点的表示法就是：
一个 $n-1$ 次 $n$ 项多项式 $f(x)$ 可以表示为：

$f(x)={\sum }_{i=0}^{n-1}{a}_i{x}^i$

所以我们可以用每一项的系数来表示 $f(x)$，即

f ( x ) = { a 0 , a 1 , a 2 , … , a n − 1 } f(x)=\{a_0,a_1,a_2,\dots,a_{n-1}\} f(x)={a0​,a1​,a2​,…,an−1​}

俗称系数表示法。

但是，当我们把这个多项式看成一个函数时，我们将 $n$ 个不同的 $x$ 带入，会得到 $n$ 个不一样的 $y$，而我们就得到了 $n$ 个点的坐标，它们确定唯一的多项式 $f(x)$

证明很简单，直接待定系数法就可以解决。

那么 $f(x)$ 还可以用这 $n$ 个点表示：

$f(x)=\{(x_0,y_0),(x_1,y_1),(x_2,y_2),\dots ,(x_{n-1},y_{n-1})\}$

(其中 $y_i=f(x_i)$)

俗称点值表示法。

多项式乘法

对于两个系数表示法表示的多项式 $f(x)$ 和 $g(x)$，如果要计算它们的乘积 $h(x)$，我们需要枚举 $f(x)$ 的每一项和 $g(x)$ 的每一项相乘，最后累计，时间复杂度 $O(n^2)$

那么换成点值表示呢？时间复杂度为 $O(n)$

Why?

设两个多项式 $f(x)$ 和 $g(x)$ 分别为：

$f(x)=\{(x_0,y{1}_0),(x_1,y{1}_1),(x_2,y{1}_2),\dots ,(x_{n-1},y{1}_{n-1})\}$

(其中 $y{1}_i=f(x_i)$)

$g(x)=\{(x_0,y{2}_0),(x_1,y{2}_1),(x_2,y{2}_2),\dots ,(x_{n-1},y{2}_{n-1})\}$

(其中 $y{2}_i=g(x_i)$)

那么结果 $h(x)$ 为：

$h(x)=\{(x_0,y{2}_0\cdot y{1}_0),(x_1,y{2}_1\cdot y{1}_1),(x_2,y{2}_2\cdot y{1}_2),\dots ,(x_{n-1},y{2}_{n-1}\cdot y{1}_{n-1})\}$

好，我们就结束了

但是怎么将系数表示法转换为点值表示法呢？

---

复数及运算

高中课本里讲过复数，不过不知道也没关系，这里会讲。

定义：复数单位$i$ 满足 $i^2=-1$，则形如 $a+bi$ 的数为复数。$(a,b\in R)$

其中 $a$ 叫做实部， $b$ 叫做虚部， $i$ 为虚数单位。

所以有 $\sqrt{-7}=\sqrt{7}i$

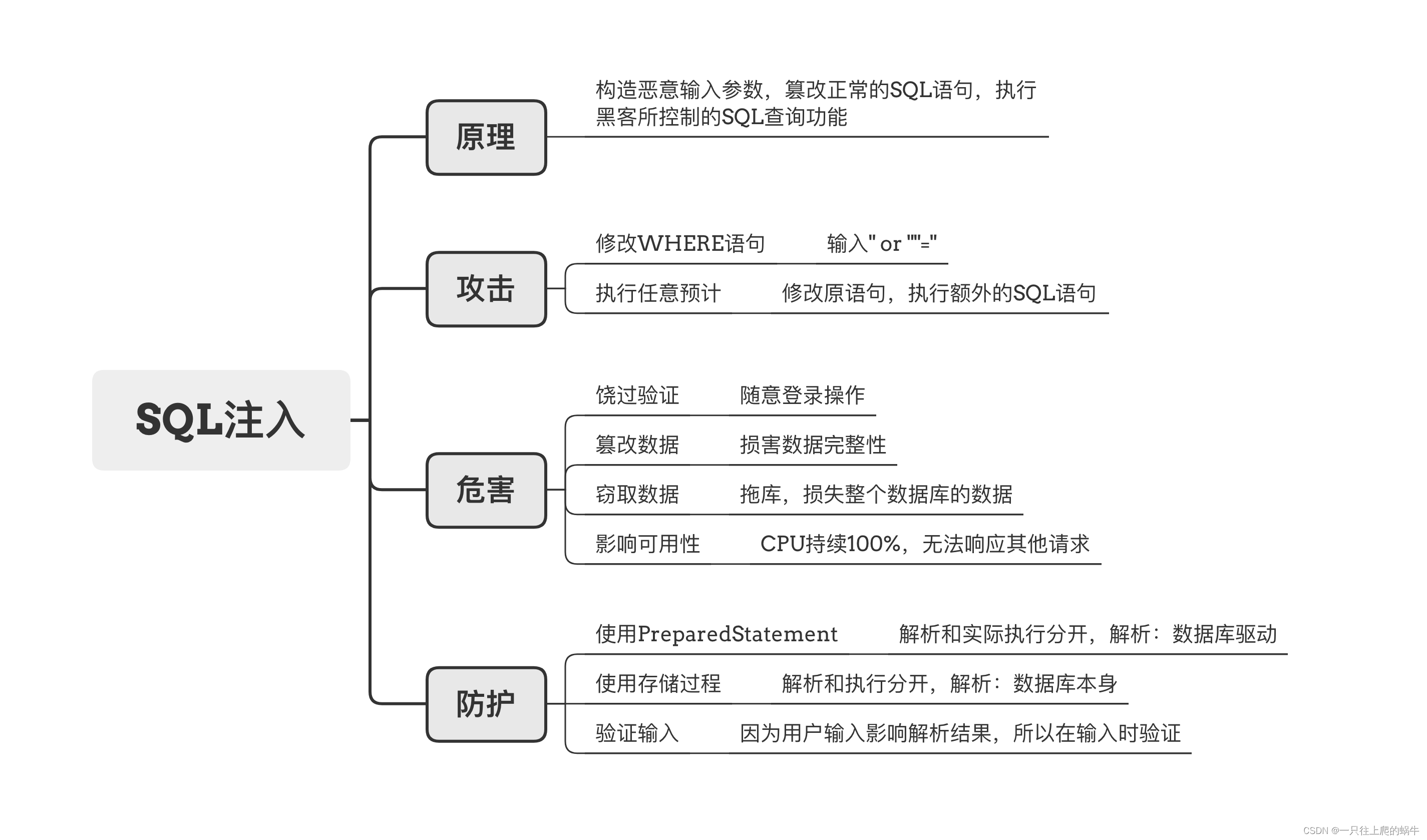
类似平面直角坐标系，在复平面直角坐标系中，复数为其中的一个点。

如下图：

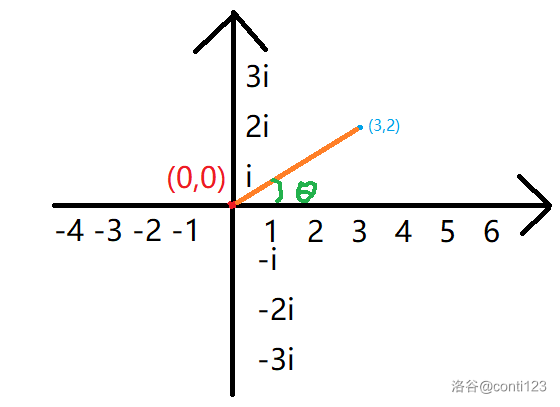
点（3,2）表示的复数为 $3+2i$

它也可以表示为（ $\sqrt{1}3,\theta$）

定义：一个复数的模为它到原点的距离。

及复数 $z=a+bi$ 的模记为 $|z|=\sqrt{a^2+b^2}$

一个复数的共轭复数为其虚部取反。

及复数 $z=a+bi$ 的共轭复数为$\bar{z}=a-bi$，$z\bar{z}=a^2+b^2$

其实就跟共轭根式差不多。

复数的运算其实跟实数的运算差不多。

设 $z_1=a+bi$，$z_2=c+di$

加减法：实部和虚部分别相加减：

$z_1\pm z_2=(a\pm c)+(b\pm d)i$

乘法：硬算出奇迹（拆完后合并同类项）

$z_1{z}_2=(ac-bd)+(bc+ad)i$

$(a_1,{\theta }_1)(a_2,{\theta }_2)=(a_1{a}_2,{\theta }_1+{\theta }_2)$

除法：化简

$\frac{z_1}{z_2}=\frac{a+bi}{c+di}=\frac{(a+bi)(c-di)}{(c+di)(c-di)}=\frac{ac-bd{i}^2+bci-adi}{c^2-d^2{i}^2}=\frac{(ac+bd)+(bc-ad)i}{c^2+d^2}$

导数

和初中的 $y=\dots$ 不一样，我们用 $f(x)$ 来表示一个关于 $x$ 的函数。

一般地，已知函数 $y=f(x)$，$x_0,x_1$ 是其定义域内不同两点，记 $\Delta x=x_1-x_0,\Delta y=y_1-y_0=f(x_1)-f(x_0)=f(x_0+\Delta x)-f(x_0)$，则当 $\Delta x\ne 0$ 时，商 $\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}=\frac{\Delta y}{\Delta x}$ 称作函数 $y=f(x)$在区间 $[x_0,x_0 +_\Delta x] $ 上的平均变化率。

当 $\Delta x$ 趋近于 $0$ 时，平均变化率 $\frac{\Delta y}{\Delta x}=\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}$ 趋近于一个常数 $l$，那么常数 $l$ 称为函数 $f(x)$ 在点 $x_0$ 的瞬时变化率。

趋近于可以用符号 $\to$ 表示，所以上面那句话可以这样表示：

当$\Delta x\to 0$ 时，$\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}\to l$

或记作：

${\lim }_{\Delta x\to 0}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}=l$

函数在 $x_0$ 的瞬时变化率，通常称为 $f(x)$ 在 $x=x_0$ 处的导数，并记作 $f^{\prime }(x_0)$。

注意，是 $f^{\prime }$。

那么对于函数 $f(x)$ 怎么求导呢？

如下：

$$\left\{\begin{array}{c}(x^a{)}^{\prime }=a{x}^{a-1}\\ (c{)}^{\prime }=0\\ (e^x{)}^{\prime }=e^x\\ (\ln x{)}^{\prime }=\frac{1}{x}\\ (\sin x{)}^{\prime }=\cos x\\ (\cos x{)}^{\prime }=\sin x\end{array}\right\}$$

例如 $f(x)=x^2$，则 $f^{\prime }(x)=2x$

最后再说一点 $f^{\prime }(x)$ 表示函数 $f(x)$ 在$x$ 取值为几时切线的斜率。

泰勒公式及展开式

泰勒公式：

$f(x)=f(x_0)+f^{\prime }(x_0)(x-x_0)+\frac{f^{\prime \prime }(x_0)}{2!}(x-x_0{)}^2+\cdots +\frac{f^{(n)}(x_0)}{n!}(x-x_0{)}^n+R_{n+1}(x)$

其中 $R$ 为误差。

那么当 $x_0=0$ 时，得到麦克劳林公式：

$f(x)=f(0)+f^{\prime }(0)x+\frac{f^{\prime \prime }(0)}{2!}{x}^2+\cdots +\frac{f^{(n)}(0)}{n!}{x}^n+R_{n+1}(x)$

所以我们就有了以下几个展开式：

$$\left\{\begin{array}{c}{e}^x=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\cdots +\frac{x^n}{n!}+\cdots \\ \ln (1+x)=x-\frac{x^2}{2}+\frac{x^3}{3}+\cdots +(-1{)}^{n-1}\frac{x^n}{n}+\cdots \\ \sin x={\sum }_{k=0}^{\infty }(-1{)}^k\frac{x^{2k+1}}{(2k+1)!}\\ \cos x={\sum }_{k=0}^{\infty }(-1{)}^k\frac{x^{2k}}{(2k)!}\end{array}\right\}$$

欧拉公式

接上文，展开 $e^{ix}$，得：
$$e^{ix}=1+ix-\frac{x^2}{2!}-i\frac{x^3}{3!}+\frac{x^4}{4!}+i\frac{x^5}{5!}-\frac{x^6}{6!}-i\frac{x^7}{7!}+\cdots )$$
$$e^{ix}=(1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+\cdots )+i(x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{7^3}{7!}+\cdots )$$

$$e^{ix}=\cos x+i\sin x$$

将 $x=\pi$ 带入：

$e^{i\pi }=\cos \pi +i\sin \pi =-1$

所以欧拉恒等式出来：

$e^{i\pi }+1=0$

单位根

设 $n$ 为正整数，若$x^n=1$ ，则 $x$ 是 $n$ 次单位根。

下文默认 $n=2^m,m$为正整数。

根据上文的欧拉公式，我们可知 $e^{2k\pi i}=\cos 2k\pi +i\sin 2k\pi =1$，故 $n$ 次单位根分别是： $e^{\frac{2k\pi i}{n}}=\cos \frac{2k\pi }{n}+i\sin \frac{2k\pi }{n},(k=0,1,2,\dots ,n-1)$。

接上文复数的知识，每个单位根在复平面上的坐标为 $(\cos \frac{2k\pi }{n},\sin \frac{2k\pi }{n})$。
如图：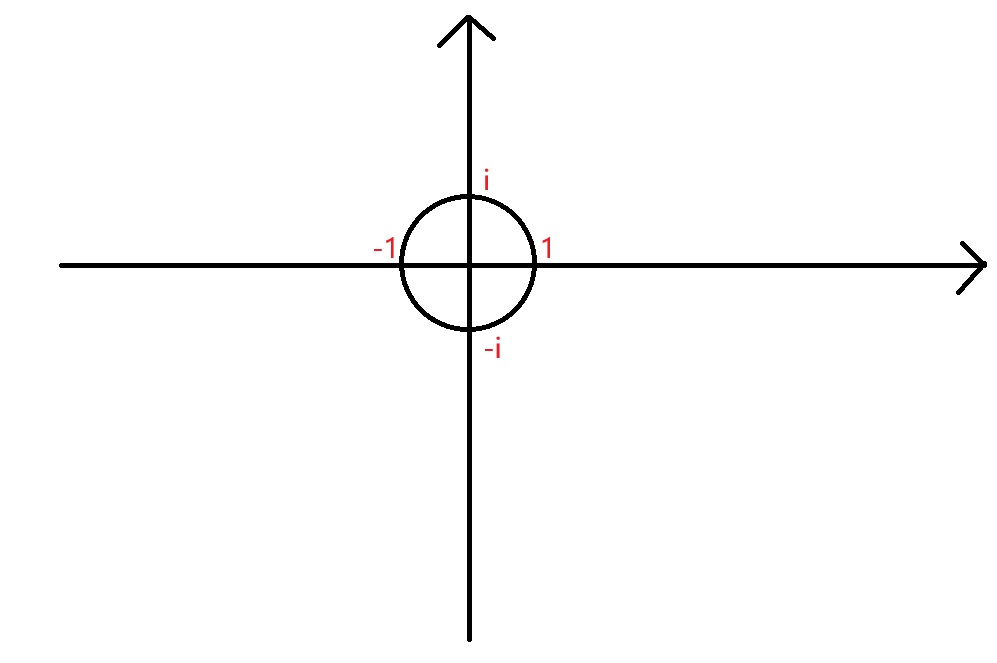

在一个标准复平面坐标系上，以 $1$ 为半径画一个圆， $n$次单位根可以想象为把这个圆平分为 $n$ 分中每一个点。

我们用${\omega }_n^1,{\omega }_n^2,{\omega }_n^3,\dots ,{\omega }_n^n$ 来表示 $n$ 次单位根的每一个根，及方程的每一个解。

所以有 ${\omega }_n^k=\cos k\frac{2\pi }{n}+i\sin k\frac{2\pi }{n}$

如当 $n=4$时，${\omega }_4=1,-1,i,-1$

如当 $n=1$ 时，${\omega }_1=1$

单位根的性质：

${\omega }_{2n}^{2k}={\omega }_n^k=-{\omega }_n^{k+\frac{n}{2}}$

${\omega }_n^0={\omega }_n^n=1$

${\omega }_{2n}^{2k}=\cos 2k\frac{2\pi }{2n}+i\sin 2k\frac{2\pi }{2n}={\omega }_n^k$

${\omega }_n^{\frac{n}{2}}=\cos \frac{n}{2}\cdot \frac{2\pi }{n}+i\sin \frac{n}{2}\cdot \frac{2\pi }{n}=\cos \pi +i\sin \pi =-1$

FFT

设 $n$ 为偶数，$k<\frac{n}{2}$。
设
$$A(x)=a_0+a_{1}x+a_2{x}^2+a_3{x}^3+\cdots +a_{n-1}{x}^{n-1}$$
$$A_1(x)=a_0+a_{2}x+a_4{x}^2+\cdots +a_{n-2}{x}^{\frac{n}{2}-1}$$
$$A_2(x)=a_1+a_{3}x+a_5{x}^2+\cdots +a_{n-1}{x}^{\frac{n}{2}-1}$$
所以有：
$$A(x)=A_1(x^2)+x{A}_2(x^2)$$
$$A({\omega }_n^k)=A_1({\omega }_n^{2k})+{\omega }_n^k{A}_2({\omega }_n^{2k})$$
$$A({\omega }_n^{k+\frac{n}{2}})=A_1({\omega }_n^{2k+n})+{\omega }_n^{k+\frac{n}{2}}{A}_2({\omega }_n^{2k+n})=A_1({\omega }_n^{2k})-{\omega }_n^k{A}_2({\omega }_n^{2k})$$

发现了什么？没错，只有后面一坨是相反的，这说明我们可以 $O(1)$ 通过第一个式子得出第二个式子

所以 $k$ 只要枚举前 $\frac{n}{2}$ 个数就可以了，问题缩小了一半，而缩小后还能继续缩小，所以我们用类似线段树的分治(递归)来解决它，时间复杂度 $O(n\log n)$

Code

void fft(int limit,complex *a,int type)
{
    if(limit==1) 
		return ;
    complex a1[limit>>1],a2[limit>>1];
    for(int i=0;i<=limit;i+=2)
        a1[i>>1]=a[i],a2[i>>1]=a[i+1];
    fft(limit>>1,a1,type);
    fft(limit>>1,a2,type);
    complex Wn=complex(cos(2.0*Pi/limit),type*sin(2.0*Pi/limit)),w=complex(1,0);
    for(int i=0;i<(limit>>1);i++,w=w*Wn)
        a[i]=a1[i]+w*a2[i],a[i+(limit>>1)]=a1[i]-w*a2[i];
}

IFFT

但是光有点值还是不够的，我们还要转换为数值，这就是 IFFT。
至于还有一个迭代优化。
我们下篇博客再讲。