分类目录：《深入理解强化学习》总目录

---

在文章《深入理解强化学习——马尔可夫决策过程：贝尔曼期望方程-[基础知识]》中我们讲到了贝尔曼期望方程，本文就举一个贝尔曼期望方程的具体例子，并给出相应代码实现。

下图是一个马尔可夫决策过程的简单例子，其中每个深色圆圈代表一个状态，一共有$s_1\sim s_5$共5个状态。黑色实线箭头代表可以采取的动作，浅色小圆圈代表动作，需要注意的是，并非在每个状态都能采取所有动作，例如在状态$s_1$，智能体只能采取“保持$s_1$”和“前往$s_2$”这两个动作，无法采取其他动作。

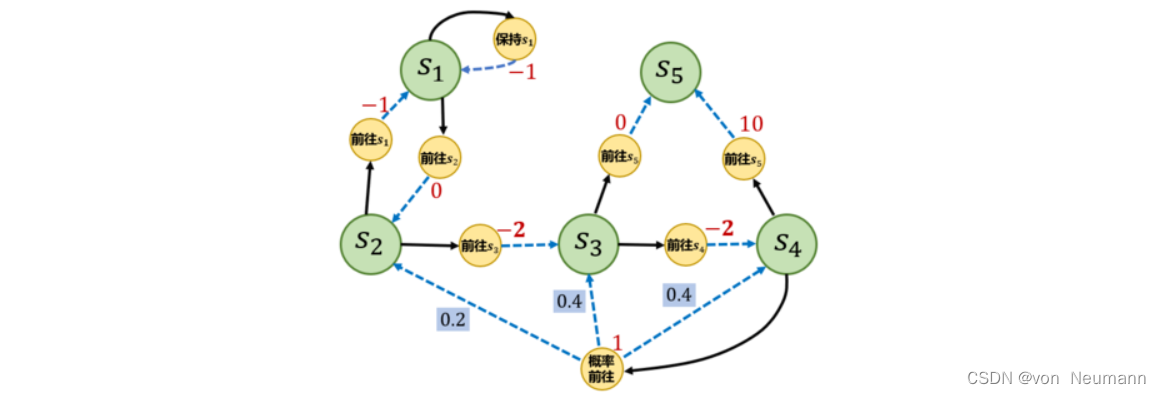
每个浅色小圆圈旁的数字代表在某个状态下采取某个动作能获得的奖励。虚线箭头代表采取动作后可能转移到的状态，箭头边上的数字代表转移概率，如果没有数字则表示转移概率为1。例如，在$s_2$下， 如果采取动作“前往$s_3$”，就能得到奖励$-2$，并且转移到$s_3$；在$s_4$下，如果采取“概率前往”，就能得到奖励$1$，并且会分别以概率$0.2,0.4,0.4$转移到$s_2$,$s_3$或$s_4$。

下面我们编写代码来表示上图中的马尔可夫决策过程，并定义两个策略。第一个策略是一个完全随机策略，即在每个状态下，智能体会以同样的概率选取它可能采取的动作。例如，在$s_1$下，智能体会以$0.5$和$0.5$的概率选取动作“保持$s_1$”和“前往$s_2$”。第二个策略是一个提前设定的一个策略：

S = ["s1", "s2", "s3", "s4", "s5"]  # 状态集合
A = ["保持s1", "前往s1", "前往s2", "前往s3", "前往s4", "前往s5", "概率前往"]  # 动作集合
# 状态转移函数
P = {
    "s1-保持s1-s1": 1.0,
    "s1-前往s2-s2": 1.0,
    "s2-前往s1-s1": 1.0,
    "s2-前往s3-s3": 1.0,
    "s3-前往s4-s4": 1.0,
    "s3-前往s5-s5": 1.0,
    "s4-前往s5-s5": 1.0,
    "s4-概率前往-s2": 0.2,
    "s4-概率前往-s3": 0.4,
    "s4-概率前往-s4": 0.4,
}
# 奖励函数
R = {
    "s1-保持s1": -1,
    "s1-前往s2": 0,
    "s2-前往s1": -1,
    "s2-前往s3": -2,
    "s3-前往s4": -2,
    "s3-前往s5": 0,
    "s4-前往s5": 10,
    "s4-概率前往": 1,
}
gamma = 0.5  # 折扣因子
MDP = (S, A, P, R, gamma)

# 策略1,随机策略
Pi_1 = {
    "s1-保持s1": 0.5,
    "s1-前往s2": 0.5,
    "s2-前往s1": 0.5,
    "s2-前往s3": 0.5,
    "s3-前往s4": 0.5,
    "s3-前往s5": 0.5,
    "s4-前往s5": 0.5,
    "s4-概率前往": 0.5,
}
# 策略2
Pi_2 = {
    "s1-保持s1": 0.6,
    "s1-前往s2": 0.4,
    "s2-前往s1": 0.3,
    "s2-前往s3": 0.7,
    "s3-前往s4": 0.5,
    "s3-前往s5": 0.5,
    "s4-前往s5": 0.1,
    "s4-概率前往": 0.9,
}


# 把输入的两个字符串通过“-”连接,便于使用上述定义的P、R变量
def join(str1, str2):
    return str1 + '-' + str2

接下来我们想要计算该马尔可夫决策过程下，一个策略$\pi$的状态价值函数。我们现在有的工具是马尔可奖励过程的解析解方法。于是，一个很自然的想法是：给定一个马尔可夫决策过程和一个策略，我们是否可以将其转化为一个马尔可夫奖励过程？答案是肯定的。我们可以将策略的动作选择进行边缘化（Marginalization)，就可以得到没有动作的马尔可夫奖励过程了。具体来说，对于某一个状态，我们根据策略所有动作的概率进行加权，得到的奖励和就可以认为是一个马尔可夫奖励过程在该状态下的奖励，即：
$$r_{‘}’(s)=\sum _{a\in A}\pi (a|s)r(s,a)$$

同理，我们计算采取动作的概率与使$s$转移到的$s^{\prime }$概率的乘积，再将这些乘积相加，其和就是一个马尔可夫奖励过程的状态从转移至的概率：
$$P^{\prime }(s^{\prime }|s)=\sum _{s\in A}\pi (a|s)P(s^{\prime }|s,a)$$

于是，我们构建得到了一个马尔可夫奖励过程$(S,P^{\prime },r^{\prime },\gamma )$。根据价值函数的定义可以发现，转化前的马尔可夫决策过程的状态价值函数和转化后的马尔可夫奖励过程的价值函数是一样的。于是我们可以用马尔可夫奖励过程中计算价值函数的解析解来计算这个马尔可夫决策过程中该策略的状态价值函数。

下面的代码计算用随机策略（也就是代码中的Pi_1）时的状态价值函数。为了简单起见，我们直接给出转化后的马尔可夫将来过程的状态转移矩阵和奖励函数：

gamma = 0.5
# 转化后的MRP的状态转移矩阵
P_from_mdp_to_mrp = [
    [0.5, 0.5, 0.0, 0.0, 0.0],
    [0.5, 0.0, 0.5, 0.0, 0.0],
    [0.0, 0.0, 0.0, 0.5, 0.5],
    [0.0, 0.1, 0.2, 0.2, 0.5],
    [0.0, 0.0, 0.0, 0.0, 1.0],
]
P_from_mdp_to_mrp = np.array(P_from_mdp_to_mrp)
R_from_mdp_to_mrp = [-0.5, -1.5, -1.0, 5.5, 0]

V = compute(P_from_mdp_to_mrp, R_from_mdp_to_mrp, gamma, 5)
print("MDP中每个状态价值分别为\n", V)

输出：

MDP中每个状态价值分别为
 [[-1.22555411]
 [-1.67666232]
 [ 0.51890482]
 [ 6.0756193 ]
 [ 0.        ]]

知道了状态价值函数$V_{\pi }(s)$后，我们可以根据以下公式计算得到动作价值函数$Q_{\pi }(s,a)$。例如$(s_4,\text{概率前往})$的动作价值为$1+0.5\times [0.2\times (-1.68)+0.4\times 0.52+0.4\times 6.08]=2.152$：
$$Q_{\pi }(s,a)=r(s,a)+\gamma \sum _{s^{\prime }\in S}P(s^{\prime }|s,a)V_{\pi }(s^{\prime })$$

这个 MRP 解析解的方法在状态动作集合比较大的时候不是很适用，那有没有其他的方法呢？第 4 章将介绍用动态规划算法来计算得到价值函数。3.5 节将介绍用蒙特卡洛方法来近似估计这个价值函数，用蒙特卡洛方法的好处在于我们不需要知道 MDP 的状态转移函数和奖励函数，它可以得到一个近似值，并且采样数越多越准确。

参考文献：
[1] 张伟楠, 沈键, 俞勇. 动手学强化学习[M]. 人民邮电出版社, 2022.
[2] Richard S. Sutton, Andrew G. Barto. 强化学习（第2版）[M]. 电子工业出版社, 2019
[3] Maxim Lapan. 深度强化学习实践（原书第2版）[M]. 北京华章图文信息有限公司, 2021
[4] 王琦, 杨毅远, 江季. Easy RL：强化学习教程 [M]. 人民邮电出版社, 2022