一、学习曲线

1. 学习曲线概述

学习曲线将训练集误差和交叉验证集误差作为训练集实例数量（m）的函数绘制而成。这意味着从较少的数据开始，逐渐增加训练集的实例数量。该方法的核心思想在于，当训练较少数据时，模型可能会完美地适应这些数据，但这并不代表它能够很好地适应交叉验证集或测试集数据。

2. 识别高偏差/欠拟合

在学习曲线中，对于高偏差或欠拟合的情况，增加训练集数据可能不会显著改善模型效果。具体而言，如果使用一条直线模型适应数据，无论训练集有多大，模型的误差都可能保持较高，表现出学习曲线趋于平稳。

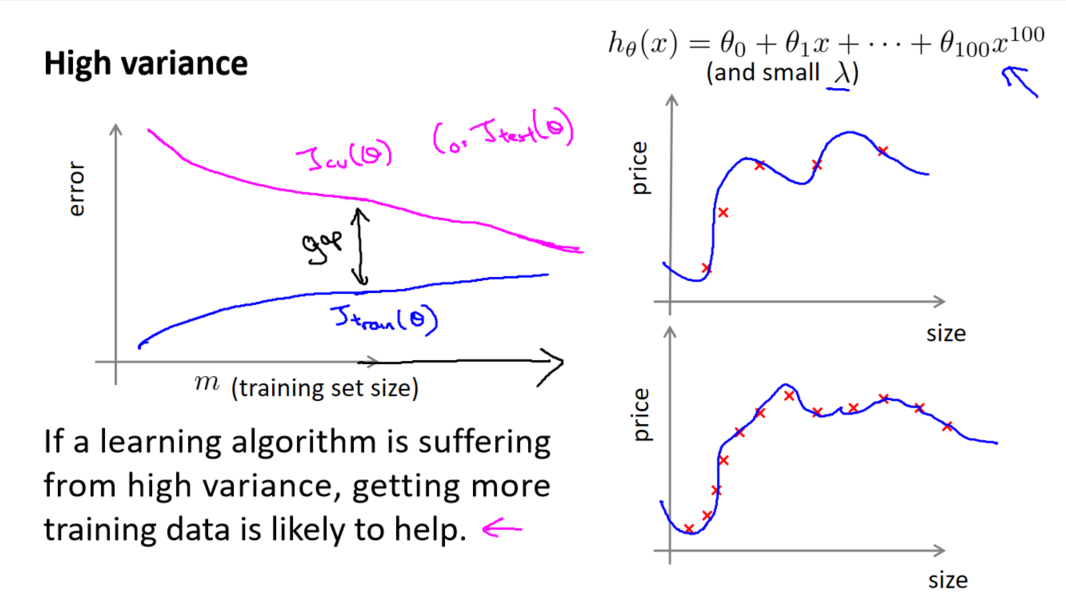
3. 识别高方差/过拟合

对于高方差或过拟合的情况，学习曲线呈现出一种特殊的模式。当交叉验证集误差远大于训练集误差时，增加更多数据到训练集可能有助于提高算法效果。高方差情况下，模型在训练集上表现很好，但泛化到未见数据时表现不佳。

4. 使用学习曲线的价值

学习曲线不仅仅是一种工具，更是算法性能的“合理检验”。通过观察曲线的形状，我们可以快速判断算法的问题所在，是偏差还是方差。这为调整算法提供了重要线索，指导我们如何改进模型的性能。

二、决定下一步做什么

在机器学习中，选择下一步的操作至关重要，而之前学到的诊断法则可以帮助更好地判断应该采取哪些方法来改进学习算法的效果。在这个过程中，可以回顾六种可选的下一步，并根据问题的性质进行选择：

1. 获得更多的训练实例 - 解决高方差：如果模型在训练集上表现良好，但在交叉验证集上误差较大，可能是因为训练实例不足导致过拟合。

2. 尝试减少特征的数量 - 解决高方差：如果模型复杂度较高，可以考虑减少特征的数量，减轻过拟合问题。

3. 尝试获得更多的特征 - 解决高偏差：如果模型欠拟合，可以考虑增加特征数量，提高模型复杂度。

4. 尝试增加多项式特征 - 解决高偏差：对于线性模型，可以尝试引入更多的多项式特征，提高模型的灵活性。

5. 尝试减少正则化程度 λ - 解决高偏差：如果模型过于正则化，可以减小正则化程度，提高模型对训练数据的拟合度。

6. 尝试增加正则化程度 λ - 解决高方差：如果模型过拟合，可以增加正则化程度，限制模型的复杂度。

对于神经网络，调整网络的大小和正则化程度也是一项重要任务。较小的神经网络可能导致高偏差，而较大的神经网络可能导致高方差。通过逐步增加隐藏层的层数，可以使用交叉验证集选择最佳的网络结构。

参考资料：

[中英字幕]吴恩达机器学习系列课程

黄海广博士 - 吴恩达机器学习个人笔记