1、悲观锁
悲观锁有点像是一位比较悲观(也可以说是未雨绸缪)的人,总是会假设最坏的情况,避免出现问题。
悲观锁总是假设最坏的情况,认为共享资源每次被访问的时候就会出现问题(比如共享数据被修改),所以每次在获取资源操作的时候都会上锁,这样其他线程想拿到这个资源就会阻塞直到锁被上一个持有者释放。也就是说,共享资源每次只给一个线程使用,其它线程阻塞,用完后再把资源转让给其它线程。
Java 中synchronized和ReentrantLock等独占锁就是悲观锁思想的实现。
public void performSynchronisedTask() {
synchronized (this) {
// 需要同步的操作
}
}
private Lock lock = new ReentrantLock();
lock.lock();
try {
// 需要同步的操作
} finally {
lock.unlock();
}
2、乐观锁
乐观锁有点像是一位比较乐观的人,总是会假设最好的情况,在要出现问题之前快速解决问题。
乐观锁总是假设最好的情况,认为共享资源每次被访问的时候不会出现问题,线程可以不停地执行,无需加锁也无需等待,只是在提交修改的时候去验证对应的资源(也就是数据)是否被其它线程修改了(具体方法可以使用版本号机制或 CAS 算法)。
Java 中java.util.concurrent.atomic包下面的原子变量类(比如AtomicInteger、LongAdder)就是使用了乐观锁的一种实现方式CAS实现的。
// LongAdder 在高并发场景下会比 AtomicInteger 和 AtomicLong 的性能更好
// 代价就是会消耗更多的内存空间(空间换时间)
LongAdder longAdder = new LongAdder();
// 自增
longAdder.increment();
// 获取结果
longAdder.sum();
3、使用选择
- 悲观锁通常多用于写比较多的情况下(多写场景,竞争激烈),这样可以避免频繁失败和重试影响性能,悲观锁的开销是固定的。不过,如果乐观锁解决了频繁失败和重试这个问题的话(比如LongAdder),也是可以考虑使用乐观锁的,要视实际情况而定。
- 乐观锁通常多于写比较少的情况下(多读场景,竞争较少),这样可以避免频繁加锁影响性能。不过,乐观锁主要针对的对象是单个共享变量(参考java.util.concurrent.atomic包下面的原子变量类)。
4、乐观锁实现
Java中的乐观锁主要有两种实现方式:CAS(Compare and Swap)和版本控制。
4.1、CAS
CAS是实现乐观锁的核心算法,它通过比较内存中的值是否和预期的值相等来判断是否存在冲突。如果存在,则返回失败;如果不存在,则执行更新操作。
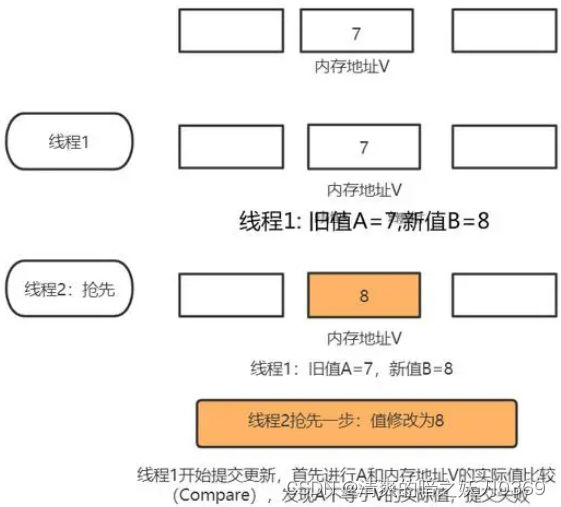
- CAS操作包括三个操作数:内存位置(V)、预期原值(A)和新值(B)。
- 当执行CAS操作时,只有当V的值等于A时,才会将V的值更新为B,否则不做任何操作。
- CAS操作是原子性的,也就是说在同一时刻只能有一个线程执行CAS操作,因此CAS机制保证了数据的一致性。
Java中提供了AtomicInteger、AtomicLong、AtomicReference等原子类来支持CAS操作。
public class Counter {
private AtomicInteger value = new AtomicInteger(0);
public void increment() {
int expect;
int update;
do {
expect = value.get();
update = expect + 1;
} while (!value.compareAndSet(expect, update));
}
}
4.2、版本控制
每当一个线程要修改数据时,都会先读取当前的版本号或时间戳,并将其保存下来。线程完成修改后,会再次读取当前的版本号或时间戳,如果发现已经变化,则说明有其他线程对数据进行了修改,此时需要回滚并重试。
public class Counter {
private int value = 0;
private int version = 0;
public void increment() {
int currentVersion;
int currentValue;
do {
currentVersion = version;
currentValue = value;
currentValue++;
} while (currentVersion != version);
value = currentValue;
version = currentVersion + 1;
}
}
5、补充
5.1、ConcurrentHashMap
ConcurrentHashMap是Java中的一个线程安全的哈希表实现,它使用分离锁(Segment)来保证线程安全。每个Segment都是一个独立的哈希表,每个操作只锁定相关的Segment,因此可以支持更高的并发性。
ConcurrentHashMap使用了一种基于CAS的技术来实现乐观锁,它通过比较当前的value和预期的value是否相等来判断是否存在冲突。如果存在,则返回失败;如果不存在,则执行更新操作。
5.2、LongAdder
在 JDK1.8 中,Java 提供了一个新的原子类 LongAdder。LongAdder 在高并发场景下会比 AtomicInteger 和 AtomicLong 的性能更好,代价就是会消耗更多的内存空间。
LongAdder 的原理就是降低操作共享变量的并发数,也就是将对单一共享变量的操作压力分散到多个变量值上,将竞争的每个写线程的 value 值分散到一个数组中,不同线程会命中到数组的不同槽中,各个线程只对自己槽中的 value 值进行 CAS 操作,最后在读取值的时候会将原子操作的共享变量与各个分散在数组的 value 值相加,返回一个近似准确的数值。