- 代码跑一遍存在什么问题?
- 什么是 O 复杂度表示法?
- 如何分析时间复杂度?
- 常见时间复杂度量级有哪些?
- O(1)
- O(logn)
- O(n)
- O(nlogn)
- O(m+n)
- O(m*n)
- O(n^2)
- O(2^n)
- O(n!)
- 不同时间复杂度差距有多大?
- 时间复杂度分析总结
- 如何分析空间复杂度?
- 实际项目开发中都会进行不同数据规模的真实测试,有没有必要进行事前的复杂度分析?
- 最好、最坏情况时间复杂度
- 平均情况时间复杂度
- 均摊时间复杂度
数据结构与算法解决的是执行更快和更省资源的问题,快和省通过复杂度来衡量。
代码跑一遍存在什么问题?
- 结果依赖环境。
- 结果受数据规模影响很大,无法覆盖所有数据场景。
需要使用复杂度分析进行粗略的估计。
什么是 O 复杂度表示法?
以C++为例子,按照语句生成机器语言指令,我们假设每个机器指令执行时间相同为 unit_time,为了方便对每个语句进行分析,将代码写成如下格式:
int func(int n)
{
int sum = 0; //1 * unit_time
for (int i = 1; //1 * unit_time
i <= n; //n * unit_time
++i) //n * unit_time
{
sum = sum + i; //n * unit_time
}
return sum;//1 * unit_time
}
执行总时间为:(3n + 3 ) unit_time
下面代码进行分析:
int func(int n)
{
int sum = 0; //1 * unit_time
for (int i = 1; //1 * unit_time
i <= n; //n * unit_time
++i) //n * unit_time
{
for (int j = 1; //n * unit_time
j <= n; //n^2 * unit_time
++j) //n^2 * unit_time
{
sum = sum + i * j;//n^2 * unit_time
}
}
return sum;//1 * unit_time
}
执行总时间为:(2 * n^2 + 3n + 3) * unit_time
结论:所有代码的执行时间 T(n)与语句执行次数f(n)成正比。
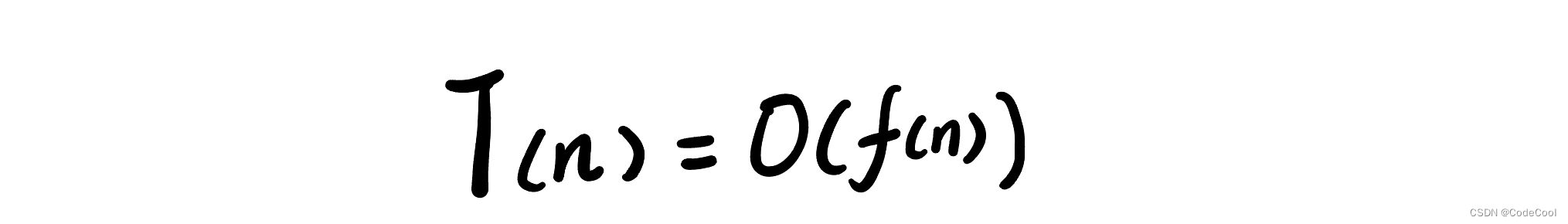
T(n):代码执行时间。
f(n):每个语句的执行次数总和。
n:数据规模。
大O表示:代码执行时间随数据规模增长的变化趋势,称为渐进时间复杂度。
公式中,高阶对于增长趋势影响最大,所以低阶、常数、系数可以忽略。
上面两个例子忽略之后:
(3n + 3 ) unit_time 时间复杂度为 O(n)。
(2 * n^2 + 3n + 3) * unit_time 时间复杂度为 O(n^2)。
如何分析时间复杂度?
只关心循环执行最多的一段代码,这段代码是最高阶量级,对增长趋势影响最大。
上面两个例子代码:
(3n + 3 ) unit_time 时间复杂度为 O(n)。
(2 * n^2 + 3n + 3) * unit_time 时间复杂度为 O(n^2)。
加法法则:不同代码段取最高阶量级。
int func(int n)
{
int sum_1 = 0; //1 * unit_time
for (int p = 1; //1 * unit_time
p < 100; //100 * unit_time
++p) //100 * unit_time
{
sum_1 = sum_1 + p; //100 * unit_time
}
//上面一段求sum_1代码时间复杂度为:302 * unit_time
int sum_2 = 0;//1 * unit_time
for (int q = 1; //1 * unit_time
q < n; //n * unit_time
++q) //n * unit_time
{
sum_2 = sum_2 + q; //n * unit_time
}
//上面一段求sum_2代码时间复杂度为:(3n + 2) * unit_time
int sum_3 = 0;//1 * unit_time
for (int i = 1; //1 * unit_time
i <= n; //n * unit_time
++i) //n * unit_time
{
for (int j = 1; //n * unit_time
j <= n; //n^2 * unit_time
++j) //n^2 * unit_time
{
sum_3 = sum_3 + i * j;//n^2 * unit_time
}
}
//上面一段求sum_3代码时间复杂度为:(3n^2 + 3n + 2) * unit_time
return sum_1 + sum_2 + sum_3;//1 * unit_time
}
三段代码时间复杂度求和为最高阶:O(n^2)。
总结: T1(n)=O(f(n)),T2(n)=O(g(n)); 那么 T(n)=T1(n)+T2(n)=max(O(f(n)), O(g(n))) =O(max(f(n), g(n)))
乘法法则:嵌套代码,嵌套内外代码复杂度的乘积。
int func(int n)
{
int num = 0; 1 * unit_time
for (int i = 1; //1 * unit_time
i <= n; //n * unit_time
++i) //n * unit_time
{
for (int j = 1; //n * unit_time
j <= n; //n^2 * unit_time
++j) //n^2 * unit_time
{
fun(n, num);//n^3 * unit_time
}
}
}
int fun(int n, int num)
{
for (int k = 1; //1 * unit_time
k <= n; //n * unit_time
++k) //n * unit_time
{
num++; //n * unit_time
}
}
func 函数执行时间复杂度为:O(n^2) * O(n) = O(n^3)
总结:T1(n)=O(f(n)),T2(n)=O(g(n));那么 T(n)=T1(n)*T2(n)=O(f(n))*O(g(n))=O(f(n)*g(n))
常见时间复杂度量级有哪些?
O(1)
代码执行时间不随数据规模 n 增大而增大,时间复杂度都为O(1)。
int func(int n)
{
int sum = 0; //1 * unit_time
for (int p = 1; //1 * unit_time
p < 100; //100 * unit_time
++p) //100 * unit_time
{
sum = sum + p; //100 * unit_time
}
}
O(logn)
下面代码:
int func(int n)
{
int i = 1;
while (i <= n)
{
i = i * 2;
}
}
i 取值为等比数量,每一次取值:
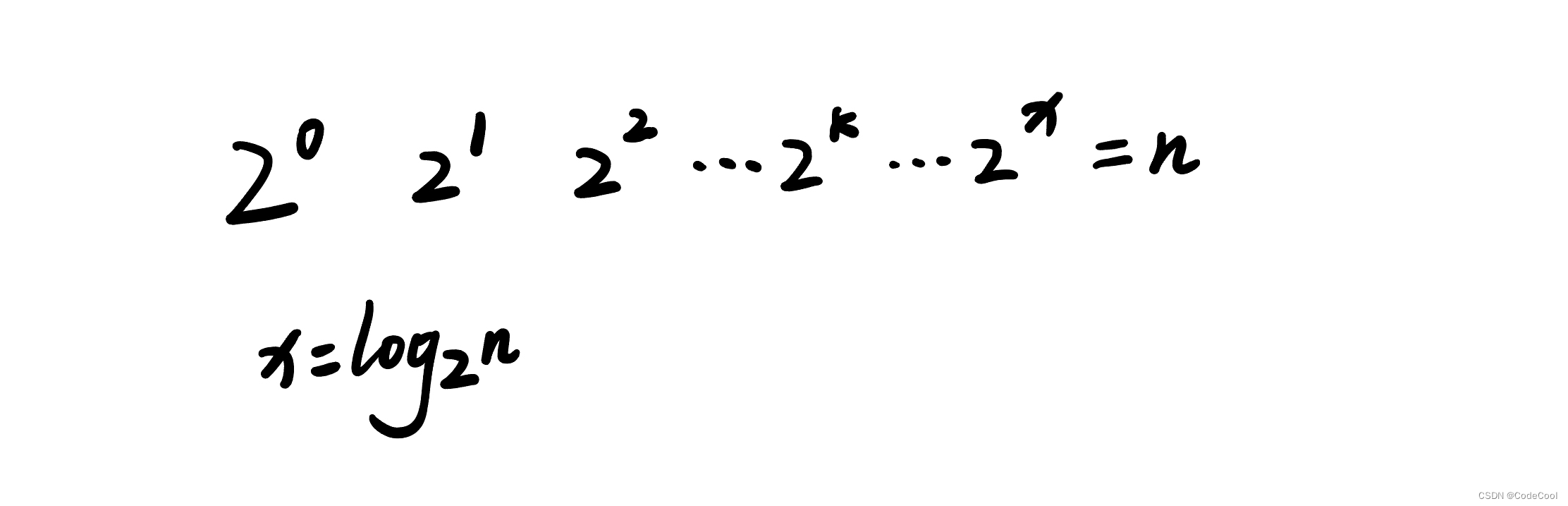
代码修改:
int func(int n)
{
int i = 1;
while (i <= n)
{
i = i * 3;
}
}
i 取值为等比数量,每一次取值:

对数阶时间复杂度中,忽略对数的 “底”,同意表示为O(logn)。
O(n)
int func(int n)
{
int sum = 0;//1 * unit_time
for (int i = 1; //1 * unit_time
i <= n; //n * unit_time
++i) //n * unit_time
{
sum++;
}
return sum;//1 * unit_time
}
单循环,最高阶量级为O(n)。
O(nlogn)
将对数嵌套在循环中:
int func(int n)
{
int i = 1;
for (int j = 0; j < n; ++j)
{
while (i <= n)
{
i = i * 2;
}
}
}
O(m+n)
int func(int m, int n)
{
int sum_1 = 0; //1 * unit_time
for (int i = 1; //1 * unit_time
i < m; //m * unit_time
++i) //m * unit_time
{
sum_1 = sum_1 + i;//m * unit_time
}
int sum_2 = 0; //1 * unit_time
for (int j = 1; //1 * unit_time
j < n; //n * unit_time
++j) //n * unit_time
{
sum_2 = sum_2 + j;//n * unit_time
}
return sum_1 + sum_2; //1 * unit_time
}
无法实现评估 m 和 n 哪个数据规模更大,所以取最高阶量级之后为:T1(m) + T2(n) = O(f(m) + g(n))。
O(m*n)
int func(int n, int m)
{
int sum = 0;//1 * unit_time
for (int i = 1; //1 * unit_time
i <= n; //n * unit_time
++i) //n * unit_time
{
for (int j = 1; //n * unit_time
j <= m; //n * m * unit_time
++m) //n * m * unit_time
{
sum = sum + i * j;//n * m * unit_time
}
}
}
乘法法则:嵌套代码,嵌套内外代码复杂度的乘积。
总结:T1(n)=O(f(n)),T2(n)=O(g(n));那么 T(n)=T1(n)*T2(n)=O(f(n))*O(g(n))=O(f(n)*g(n))
O(n^2)
int func(int n)
{
int sum = 0;//1 * unit_time
for (int i = 1; //1 * unit_time
i <= n; //n * unit_time
++i) //n * unit_time
{
for (int j = 1; //n * unit_time
j <= n; //n^2 * unit_time
++j) //n^2 * unit_time
{
sum = sum + i * j;//n^2 * unit_time
}
}
return sum;//1 * unit_time
}
乘法法则:嵌套代码,嵌套内外代码复杂度的乘积。
总结:k层嵌套时间复杂度为O(n^k)。
O(2^n)
int fibonacci(int n)
{
if (n <= 1)
{
return n;
}
return fibonacci(n - 1) + fibonacci(n - 2);
}
上面代码获取斐波那契数列的第 n 个元素,每个 fibonacci 函数都递归的调用自己 2 次。时间复杂度为O(2^n)。
O(n!)
#include <iostream>
#include <vector>
using namespace std;
void permute(vector<int>& nums, int start, int end)
{
if (start == end)
{
for (int i = 0; i < nums.size(); i++)
{
cout << nums[i] << " ";
}
cout << endl;
}
else
{
for (int i = start; i <= end; i++)
{
swap(nums[start], nums[i]);
permute(nums, start + 1, end);
swap(nums[start], nums[i]);
}
}
}
int main() {
int n;
cout << "请输入整数n: ";
cin >> n;
vector<int> nums(n);
for (int i = 0; i < n; i++) {
nums[i] = i + 1;
}
permute(nums, 0, n - 1);
return 0;
}
上面代码输出全排列,permute 总共会有 n! 次函数调用。时间复杂度为 O(n!)。
不同时间复杂度差距有多大?
时间复杂度分析总结
单段代码看高频:比如循环。
多段代码取最大:比如一段代码中有单循环和多重循环,那么取多重循环的复杂度。
嵌套代码求乘积:比如递归、多重循环等
多个规模求加法:比如方法有两个参数控制两个循环的次数,那么这时就取二者复杂度相加。
如何分析空间复杂度?
算法的存储空间随数据规模的变化趋势,称为渐进空间复杂度。
void func(int n)
{
int* a = new int[n];
for (int i = 0; i < n; ++i)
{
a[i] = i ;
}
}
上面代码,空间复杂度为O(n),
常见的空间复杂度就是 O(1)、O(n)、O(n2 )。
实际项目开发中都会进行不同数据规模的真实测试,有没有必要进行事前的复杂度分析?
有必要。
提供了理论分析方向和效率上的感性认识。
不会浪费很多时间。
有这种理论分析的思维,写代码时会尽可能去寻找最优解,也有助于产出性能更高的程序,降低系统开发和维护的成本。
不依赖于环境。
最好、最坏情况时间复杂度
// n表示数组array的长度
int find(int* array, int n, int x)
{
int i = 0;
int pos = -1;
for (; i < n; ++i)
{
if (array[i] == x)
{
pos = i;
break;
}
}
return pos;
}
最好情况,第一个元素时查找的变量 x,时间复杂度:O(1)。
最坏情况,没有查找到变量x,遍历整个数字,时间复杂度:O(n)。
平均情况时间复杂度
// n表示数组array的长度
int find(int* array, int n, int x)
{
int i = 0;
int pos = -1;
for (; i < n; ++i)
{
if (array[i] == x)
{
pos = i;
break;
}
}
return pos;
}
总共有 n + 1种情况:
- 在数组 0 ~ n - 1。
- 不在数组中。
在数组中概率为1/2,
不在数组中概率为1/2。
平均时间复杂度:
TODO
同一段代码在不同情况下有数量级的差距时才详细分析最好、最坏和平均时间复杂度。
均摊时间复杂度
int* m_array = new int[N];
int m_count = 0;
void insert(int val)
{
if (m_count == N)
{
int sum = 0;
for (int i = 0; i < N; ++i)
{
sum = sum + m_array[i];
}
m_array[0] = sum;
m_count = 1;
}
m_array[m_count] = val;
++m_count;
}
向 m_array 插入元素,元素满时将 m_array 当前所有元素值相加放在数组第一个位置。
最好情况时间复杂度,数组未满:O(1)。
最坏情况时间复杂度,数组满:O(n)。
平均情况时间复杂度:
数组中有空闲时,有n种情况,时间复杂度为O(1)。数组中没有空闲时时间复杂度为O(n),总共 n + 1 中情况出现的概率相同。
根据加权平均计算平均时间复杂度为:
TODO
可以使用摊还分析的情况:
- 算法大部分操作时间复杂度低,只有个别操作时间复杂度高。
- 时间复杂度低的操作和时间复杂度高的操作有时序关系且循环往复。
一般均摊时间复杂度等于最好情况时间复杂度。