Leetcode98 验证二叉搜索树

news2024/9/29 19:14:16

题意理解：

首先明确二叉树的定义，对于所有节点，根节点的值大于左子树所有节点的值，小于右子树所有节点的值。

注意一个误区：

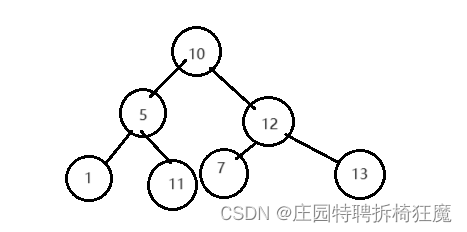
根节点简单和左孩子，右孩子比大小是不够的，要和子树比，如下图：

他每个节点根节点大于左孩子，小于右孩子。

但是他的每个根节点不大于左子树的所有节点的值，小于右子树所有节点的值，它是无序的，不是一颗二叉搜索树.

二叉搜索树的特点：

二叉搜索树的中序遍历是单调递增的数列。

1.数列递增判断【其实也是递归】

已知二叉搜索树的中序遍历的单调递增的，所以只要判断二叉树中序遍历数列是否单调递增即可。

//一个合法的搜索二叉树的中序遍历应该是严格的递增数列
    List<Integer> reuslt=new ArrayList<>();
    public boolean isValidBST(TreeNode root) {
        if(root==null) return true;
        //中序遍历是递增序列
        //左节点处理
        boolean left=isValidBST(root.left);
        //根节点处理
            //数列为空的时候，直接往进加
            //数列不为空的时候与数列最后一位的值比大小，
            //  比它大则说明单调递增
            //  比它小则说明不符合单调递增，返回false
        if(reuslt.size()==0||reuslt.get(reuslt.size()-1)< root.val){
            reuslt.add(root.val);
        }else{
            return false;
        }
        //右节点处理
        boolean right=isValidBST(root.right);
        return left&right;
    }

2.递归

//递归
    //为什么用long?
    //因为节点值-2^31 <= Node.val <= 2^31 - 1,囊括了int范围所有值
    //maxValue初始为比int最小值还小的值
    //故取long的最小值，long的取值范围比int更广
    Long maxValue=Long.MIN_VALUE;
    public boolean isValidBST2(TreeNode root) {
        if(root==null) return true;
        //中序遍历
        //左子树验证
        boolean left=isValidBST2(root.left);
        //中节点处理
        //  maxValue总是保存当前递增的最大值
        //  当前值比maxValue大，则说明符合单调递增，将当前值给maxValue
        //  当前值比maxValue小，则说明不符合单调递增，返回false
        if(maxValue<root.val) maxValue=(long)root.val;
        else return false;
        //右子树验证
        boolean right=isValidBST2(root.right);
        return left&right;
    }

3.递归+双指针优化

把maxValue改为使用 TreeNode pre,来指向遍历的前一个节点，root总是指向当前节点，不需要复杂的考虑long还是int的问题，其余地方其实是一样的。

//递归+双指针
    TreeNode pre=null;
    public boolean isValidBST3(TreeNode root) {
        if(root==null) return true;
        boolean left=isValidBST3(root.left);
        if(pre==null||pre.val< root.val) pre=root;
        else return false;
        boolean right=isValidBST3(root.right);
        return left&right;
    }

4.迭代

迭代还是之前遍历的套路，需要使用栈保存节点，模拟递归，会有一点麻烦。

public boolean isValidBST4(TreeNode root) {
        if(root==null) return true;
        //模拟递归的栈
        Stack<TreeNode> stack=new Stack<>();
        stack.push(root);
        TreeNode pre=null;
        while(!stack.isEmpty()){
            TreeNode tmpRoot=stack.peek();
            //当前节点是否为空？
            if(tmpRoot!=null){
                //若节点不为空，则弹出当前节点
                //由于栈总是先进后出，故左中右节点的入栈顺序应为：右中左
                //为了识别中节点，在中间节点入栈后，加入一个null值，所有null值后总是中间节点，用于判断。
                //左右节点不为空时，入栈，所以左右节点不会引入null值
                stack.pop();
                if(tmpRoot.right!=null)stack.push(tmpRoot.right);
                stack.push(tmpRoot);
                stack.push(null);
                if(tmpRoot.left!=null)stack.push(tmpRoot.left);
            }else{
                //若当前节点为空，则只有可能我们是在之前的操作中引入的null值
                //将当前null值弹出后，取下一位进行比较
                //若遍历前一位节点为空或当前节点大于pre节点值，则将当前节点给pre
                //否则：当前节点小于pre的值，不符合单调增，返回false
                stack.pop();
                TreeNode tmp=stack.pop();
                if(pre==null||tmp.val>pre.val) pre=tmp;
                else return false;
            }
        }
        return true;
    }