11.盛最多的水的容器

news2024/11/9 2:39:48

一、题目

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

题目难度：中等

示例：

输入：[1,8,6,2,5,4,8,3,7]
输出：49 
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

图解：

二、题目解析

方法一：暴力枚举

定义一个最大值max用来记录容器的最大值，两层for循环，第一层控制容器的左边，第二层控制容器的右边，计算容器的容量sum，sum与max比较将最大值赋值给max，最后返回max；

public static int maxArea1(int[] height) {
        int max=0;
        for(int i=0;i<height.length-1;i++)
        {
            for(int j=i+1; j<height.length;j++)
            {
                int sum=(j-i)*Math.min(height[i],height[j]);
                max=Math.max(sum,max);
            }
        }
        return max;
    }

注意：

复杂度是O（n*2）复杂度过大，会报出超时的错误（家人们，我替你们试过了，会报错）

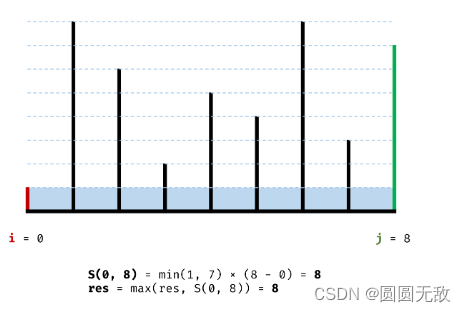
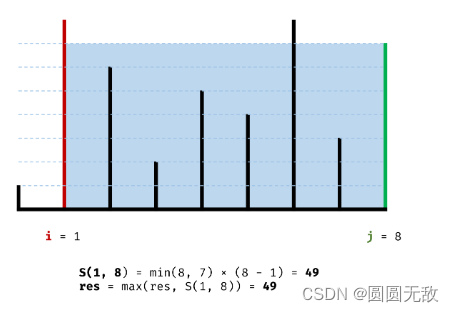
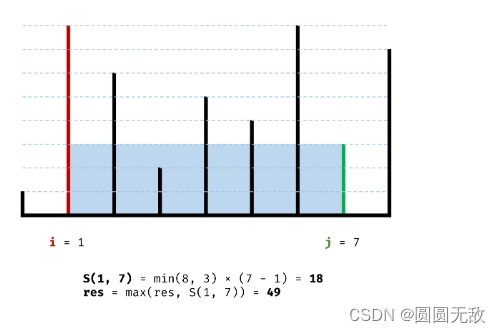
方法二：单调性+双指针

单调性：

举个例子：6，2，5，4】6为左边容器，4为右边容器，体积为3*4=12；

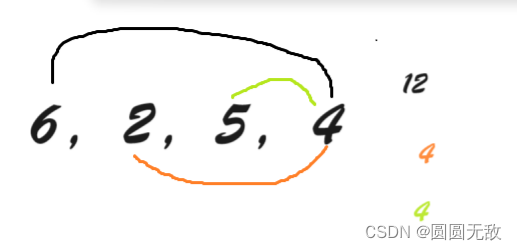
有两种情况：1.数字越来越小：宽与高都在减小

2.数字不变小：宽减小

总的来说往里去会减小，所以我们保留每一次的最大边

如图：

算法实现：

首先定义两个指针left，reight，从两头开始遍历，再定义一个变量max来存放最大值

计算容积的公式是：int sum=(reight-left)*Math.min(height[left],height[reight]);

 public static int maxArea(int[] height) {
        int max=0;
        int left=0;
        int reight=height.length-1;
        while (left<reight)
        {

            int sum=(reight-left)*Math.min(height[left],height[reight]);
            max=Math.max(max,sum);
            if(height[left]>=height[reight])
            {
                reight--;
            }
            else
            {
                left++;
            }
        }
        return max;
    }