使用最小花费爬楼梯
题目描述
给你一个整数数组 cost ,其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用,即可选择向上爬一个或者两个台阶。
你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。
请你计算并返回达到楼梯顶部的最低花费。
示例 1:
输入:cost = [10,15,20]
输出:15
解释:你将从下标为 1 的台阶开始。
- 支付 15 ,向上爬两个台阶,到达楼梯顶部。
总花费为 15 。
示例 2:
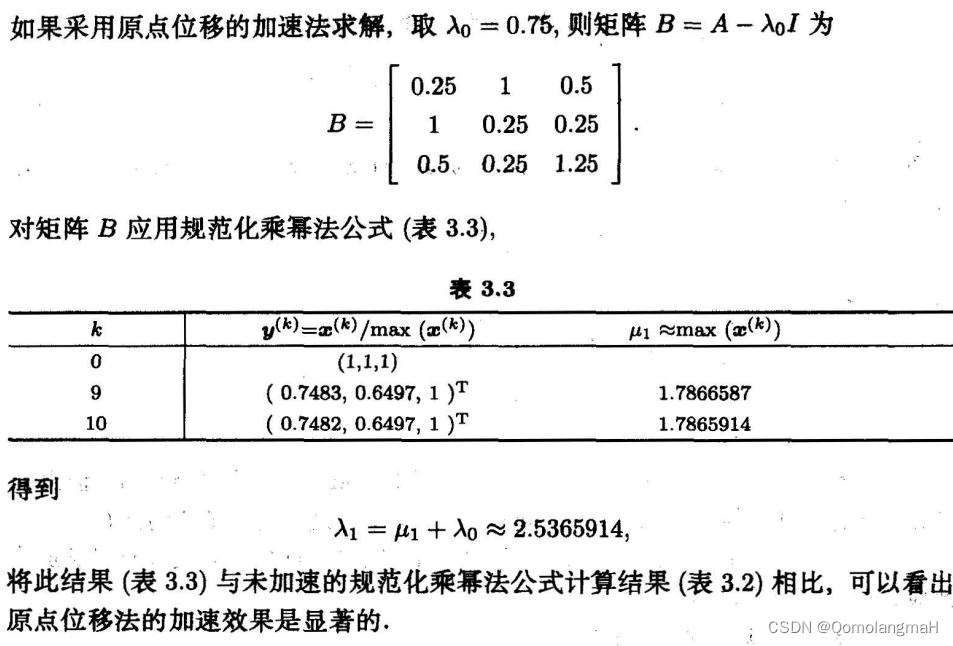
输入:cost = [1,100,1,1,1,100,1,1,100,1]
输出:6
解释:你将从下标为 0 的台阶开始。
- 支付 1 ,向上爬两个台阶,到达下标为 2 的台阶。
- 支付 1 ,向上爬两个台阶,到达下标为 4 的台阶。
- 支付 1 ,向上爬两个台阶,到达下标为 6 的台阶。
- 支付 1 ,向上爬一个台阶,到达下标为 7 的台阶。
- 支付 1 ,向上爬两个台阶,到达下标为 9 的台阶。
- 支付 1 ,向上爬一个台阶,到达楼梯顶部。
总花费为 6 。
提示:
2 <= cost.length <= 10000 <= cost[i] <= 999
动态规划五部曲
- 确定dp数组以及下标的含义
使⽤动态规划,就要有⼀个数组来记录状态,本题只需要⼀个⼀维数组dp[i]就可以了。
dp[i]的定义:到达第i台阶所花费的最少体⼒为dp[i]。 - 确定递推公式
可以有两个途径得到dp[i],⼀个是dp[i-1] ⼀个是dp[i-2]。
dp[i - 1] 跳到 dp[i] 需要花费 dp[i - 1] + cost[i - 1]。
dp[i - 2] 跳到 dp[i] 需要花费 dp[i - 2] + cost[i - 2]。
那么究竟是选从dp[i - 1]跳还是从dp[i - 2]跳呢?
⼀定是选最⼩的,所以dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]); - dp数组如何初始化
题⽬描述中明确说了 “你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。” 也就是说 到达 第 0 个台阶是不花费的,但从 第0 个台阶 往上跳的话,需要花费 cost[0]。
所以初始化 dp[0] = 0,dp[1] = 0; - 确定遍历顺序
最后⼀步,递归公式有了,初始化有了,如何遍历呢?
本题的遍历顺序其实⽐较简单,简单到很多同学都忽略了思考这⼀步直接就把代码写出来了。
因为是模拟台阶,⽽且dp[i]由dp[i-1]dp[i-2]推出,所以是从前到后遍历cost数组就可以了。 - 举例推导dp数组
拿示例2:cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1] ,来模拟⼀下dp数组的状态变化,如下:
如果
代码
力扣提交代码
c++
class Solution {
public:
int minCostClimbingStairs(vector<int>& cost) {
vector<int> dp(cost.size() + 1);
dp[0] = 0; // 默认第⼀步都是不花费体⼒的
dp[1] = 0;
for (int i = 2; i <= cost.size(); i++) {
dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
}
return dp[cost.size()];
}
};
c语言
int minCostClimbingStairs(int* cost, int costSize)
{
int dp[1010]={0};//dp[0]=0,dp[1]=0 你可以从第一个台阶和第二个台阶开始往上爬,默认第一一步不消费体力
int coust=0;
for(int i=2;i<=costSize;i++)
{
dp[i]=dp[i-1]+cost[i-1]<dp[i-2]+cost[i-2]?dp[i-1]+cost[i-1]:dp[i-2]+cost[i-2];
}
return dp[costSize];
}
总代码
#include<bits/stdc++.h>
using namespace std;
int minCostClimbingStairs(int* cost, int costSize)
{
int dp[1010]={0};//dp[0]=0,dp[1]=0 你可以从第一个台阶和第二个台阶开始往上爬,默认第一一步不消费体力
int coust=0;
for(int i=2;i<=costSize;i++)
{
dp[i]=min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);
}
return dp[costSize];
}
int main()
{
int cost[1010]={0};
int costsize=0;
scanf("cost = ");
while(1)
{
char a;
scanf("%c",&a);
if(a==']')
break;
scanf("%d",&cost[costsize]);
costsize++;
}
printf("%d",minCostClimbingStairs(cost,costsize));
return 0;
}