矩阵的特征值（eigenvalue）和特征向量（eigenvector）在很多应用中都具有重要的数学和物理意义。

  本文将详细介绍乘幂法的基本原理和步骤，并给出其Python实现。

一、Jacobi 旋转法

  Jacobi 旋转法的每一次迭代中，需要选择一个非对角元素最大的位置，然后构造相应的旋转矩阵，进行相似变换，使得矩阵逐渐对角化。

【计算方法与科学建模】矩阵特征值与特征向量的计算（一）：Jacobi 旋转法及其Python实现

二、Jacobi 过关法

  Jacobi 过关法（Jacobi’s threshold method）是 Jacobi 旋转法的一种改进版本，其主要目的是减少计算工作和提高运行速度。该方法通过动态调整阈值，并根据阈值对非对角元素进行选择性的旋转变换，以逐步对角化对称矩阵。
【计算方法与科学建模】矩阵特征值与特征向量的计算（二）：Jacobi 过关法及其Python实现（Jacobi 旋转法的改进）

三、Householder 方法

  如果对任意向量 $z$，我们可以将其分解为与 $u$ 平行的分量 $au$ 和与 $u$ 正交的分量 $bv$，即 $z=au+bv$，那么 Householder 变换会将 $z$ 变换为 $-au+bv$。这个变换可以理解为镜面反射，它不改变向量在与 $u$ 正交的平面上的投影，但将向量沿着 $u$ 的方向反射。数学表达式为：

$$Hz=au+bv\to -au+bv$$

  这个性质使得 Householder 变换在一些数值计算的应用中非常有用，例如矩阵三对角化、 QR 分解等。
【计算方法与科学建模】矩阵特征值与特征向量的计算（三）：Householder方法及其Python实现

四、乘幂法

四、乘幂法的加速

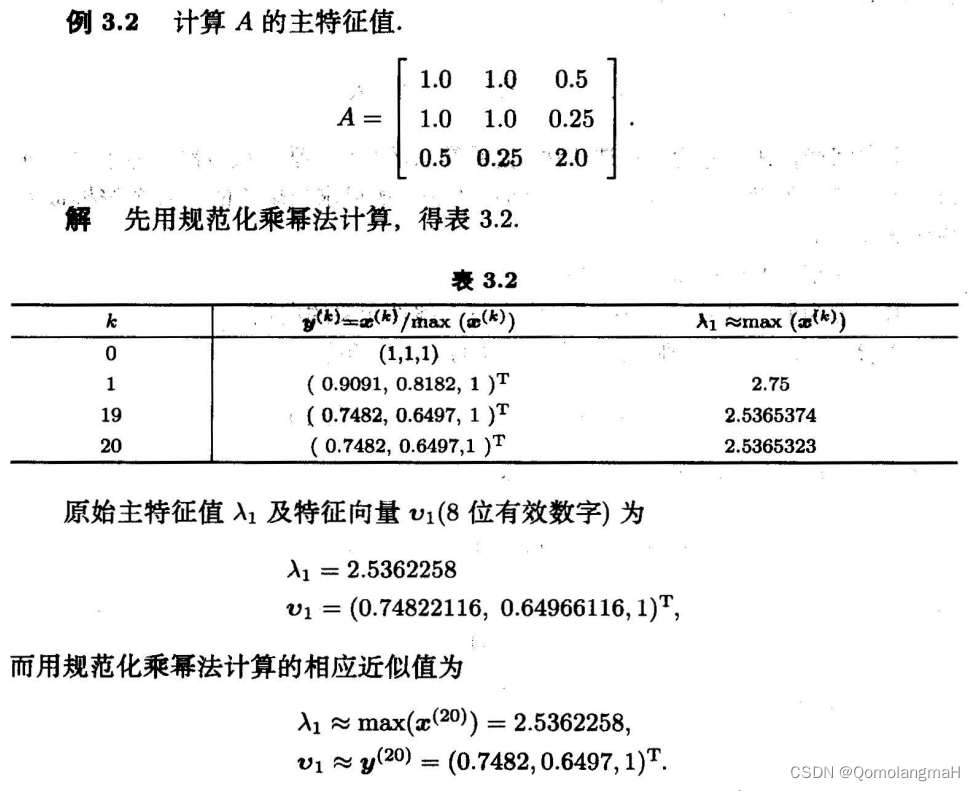
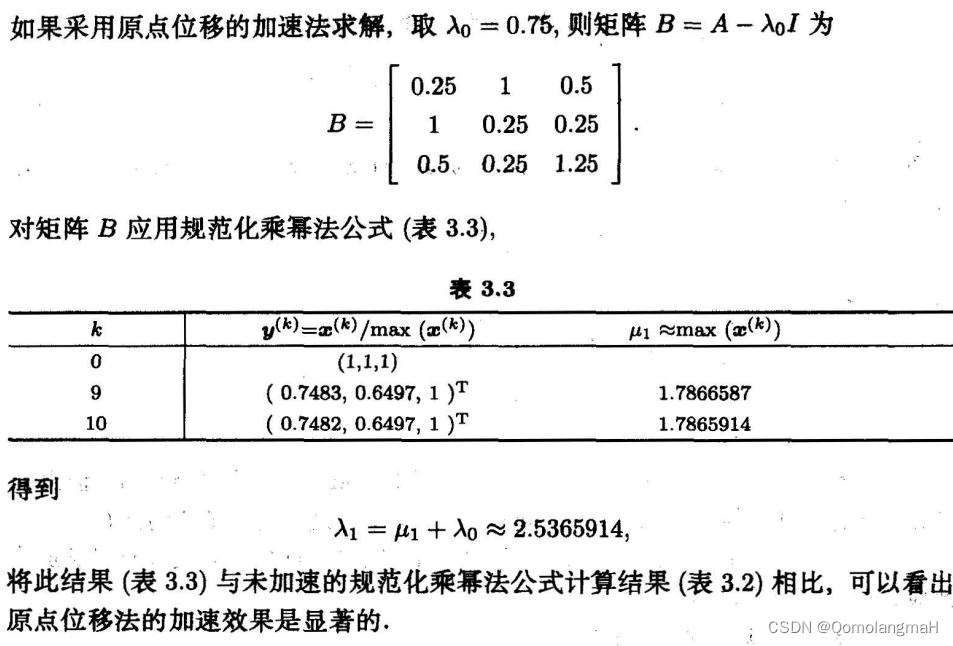
占坑：乘幂法的加速具体内容，待明日完善……