MATLAB中FFT频谱分析使用详解

news2024/11/26 12:52:31

文章目录

  • 语法
  • 说明
  • 语法一：Y = fft(X)
    • fft(X)返回X长度的傅里叶变换
  • 语法二：Y = fft(X,N)
    • 如果 X的长度小于 N，则为 X补上尾零以达到长度 N(FFT插值)
      • 双边谱转换为单边谱
    • 如果 X 的长度大于 N，则对 X 进行截断以达到长度 N。
  • 语法三：Y = fft(X,N,dim)
  • 相位
  • 补充
    • 向量的离散傅里叶变换
    • 频谱泄露的解释

本文对matlab中fft的使用作出详细说明，并对频谱的双边、单边幅度谱与相位谱加以说明。

语法

Y = fft(X)
Y = fft(X,N)
Y = fft(X,N,dim)

说明

FFT是DFT的快速算法，当FFT点数为2的整数次幂时，MATLAB可以使用FFT的快速算法；如果不是2的整数次幂，那么只能使用公式的算法，实质上未使用上快速算法，两者在计算时间上有差异。

1.Y = fft(X) 用快速傅里叶变换 (FFT) 算法计算 X 的离散傅里叶变换 (DFT)。

  • 如果 X 是向量，则 fft(X) 返回该向量的傅里叶变换。即对于 Y = fft(X) 或 Y = fft(X,[],dim)，Y的大小等于 X 的大小。
  • 如果 X 是矩阵，则 fft(X) 将 X 的各列视为向量，并返回每列的傅里叶变换。
  • 如果 X 是一个多维数组，则 fft(X) 将沿大小不等于 1 的第一个数组维度的值视为向量，并返回每个向量的傅里叶变换。

2.Y = fft(X,N) 返回 N 点 DFT。即对于 Y = fft(X,n,dim)，size(Y,dim)的值等于 n，而所有其他维度的大小保持与在 X中相同。

  • 如果 X 是向量且 X 的长度小于 N，则为 X 补上尾零以达到长度 N。(下文有举例)
  • 如果 X 是向量且 X 的长度大于 N，则对 X 进行截断以达到长度 N。(下文有举例)
  • 如果 X 是矩阵，则每列的处理与在向量情况下相同。
  • 如果 X 为多维数组，则大小不等于 1 的第一个数组维度的处理与在向量情况下相同。

3.Y = fft(X,N,dim) 返回沿维度 dim 的傅里叶变换。例如，如果 X 是矩阵，则 fft(X,N,2) 返回每行的 N 点傅里叶变换。(下文有举例)

接下来对上述三种用法进行举例，实际绘制频谱中频谱分为单边谱和双边谱的绘制，在三种用法举例中顺带将这两种绘制方式一并列出了。

语法一：Y = fft(X)

fft(X)返回X长度的傅里叶变换

使用傅里叶变换求噪声中隐藏的信号的频率分量,其中使用单边谱的绘制方式呈现频谱图。

例：指定信号的参数，采样频率为 1 kHz，信号持续时间为 1.5 秒(即1500个信号点)。

clear all;close all;clc; %清理工作区，关闭所有窗口，清空文本

Fs = 1000;            % Sampling frequency                    
T = 1/Fs;             % Sampling period       
L = 1500;             % Length of signal
t = (0:L-1)*T;        % Time vector

%构造一个信号，其中包含幅值为 0.7 的 50 Hz 正弦量和幅值为 1 的 150 Hz 正弦量。
S = 0.7*sin(2*pi*50*t) + sin(2*pi*150*t);
X = S + 2*randn(size(t));%用均值为零、方差为 4 的白噪声扰乱该信号。

%% 绘制时域信号图
%在时域中绘制含噪信号。通过查看信号 X(t) 很难确定频率分量。
subplot(141);
plot(t,X);
title("Signal Corrupted with Zero-Mean Random Noise")
xlabel("t (seconds)")
ylabel("X(t)")

subplot(143);
plot(t,S);
title("Original Signal")
xlabel("t (seconds)")
ylabel("X(t)")

%% 计算加噪声信号的傅里叶变换
Y = fft(X);%此用法的fft点数为X的点数即1500
N = L;%fft点数为信号长度
%计算双侧频谱 P2。然后基于 P2 和偶数信号长度 L 计算单侧频谱 P1。
P2 = abs(Y/N);%/N是对幅度的修正
P1 = P2(1:N/2+1);
P1(2:end-1) = 2*P1(2:end-1);%第一个点为直流分量,是真实的幅值，保持不变；从第二个开始*2，由于DFT具有对称性看单边需要*2
f = (0:(N/2))*Fs/N;%其中Fs/N为频率分辨率

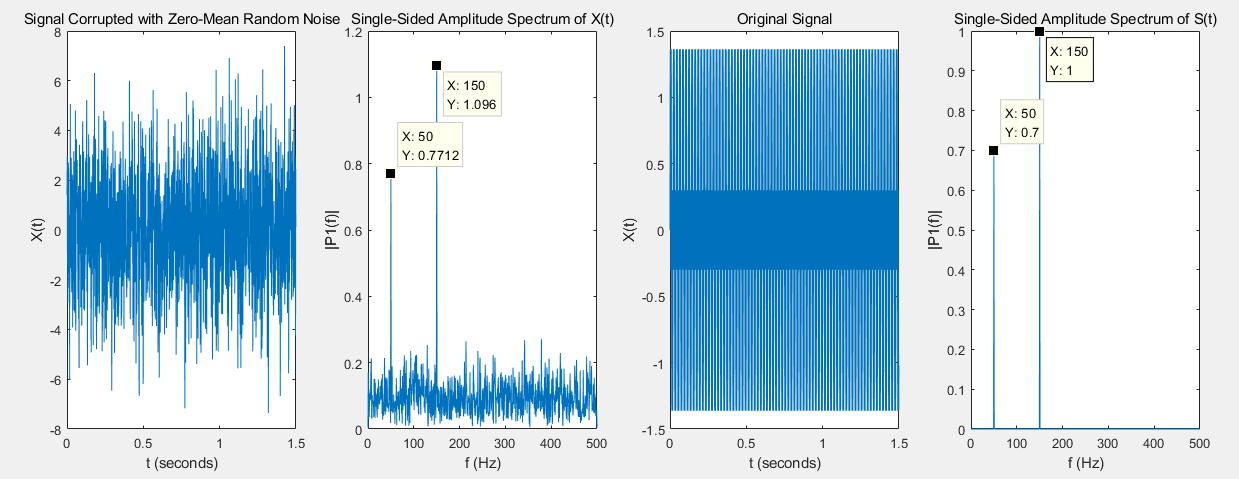
%定义频域 f 并绘制单侧幅值频谱 P1。与预期相符，由于增加了噪声，幅值并不精确等于 0.7 和 1。一般情况下，较长的信号会产生更好的频率逼近值。
subplot(142);
plot(f,P1) 
title("Single-Sided Amplitude Spectrum of X(t)")
xlabel("f (Hz)")
ylabel("|P1(f)|")

%% 现在，采用原始的、未破坏信号的傅里叶变换并检索精确幅值 0.7 和 1.0。
Y = fft(S);
P2 = abs(Y/N);
P1 = P2(1:N/2+1);
P1(2:end-1) = 2*P1(2:end-1);

subplot(144);
plot(f,P1) 
title("Single-Sided Amplitude Spectrum of S(t)")
xlabel("f (Hz)")
ylabel("|P1(f)|")

使用fft(X)求得频谱绘制的单边谱如下：
在这里插入图片描述

语法二：Y = fft(X,N)

如果 X的长度小于 N，则为 X补上尾零以达到长度 N(FFT插值)

通过填充零来对信号的傅里叶变换进行插值。

例：指定信号的参数，采样频率为 80 Hz，信号持续时间为 0.8 秒。

clear all;close all;clc; %清理工作区，关闭所有窗口，清空文本
Fs = 80;
T = 1/Fs;
L = 65;
t = (0:L-1)*T;

%创建一个 2 Hz 正弦信号及其高次谐波的叠加。该信号包含一个 2 Hz 余弦波、一个 4 Hz 余弦波和一个 6 Hz 正弦波。
X = 3*cos(2*pi*2*t) + 2*cos(2*pi*4*t) + sin(2*pi*6*t);

%在时域中绘制该信号。
subplot(131);
figure(1);
plot(t,X)
title("Signal superposition in time domain")
xlabel("t (ms)")
ylabel("X(t)")

%计算信号的傅里叶变换。
Y = fft(X);%不补零时

%计算信号的单侧幅值频谱。
f1 = Fs*(0:(L-1)/2)/L;
P2 = abs(Y/L);
P1 = P2(1:(L+1)/2);
P1(2:end) = 2*P1(2:end);

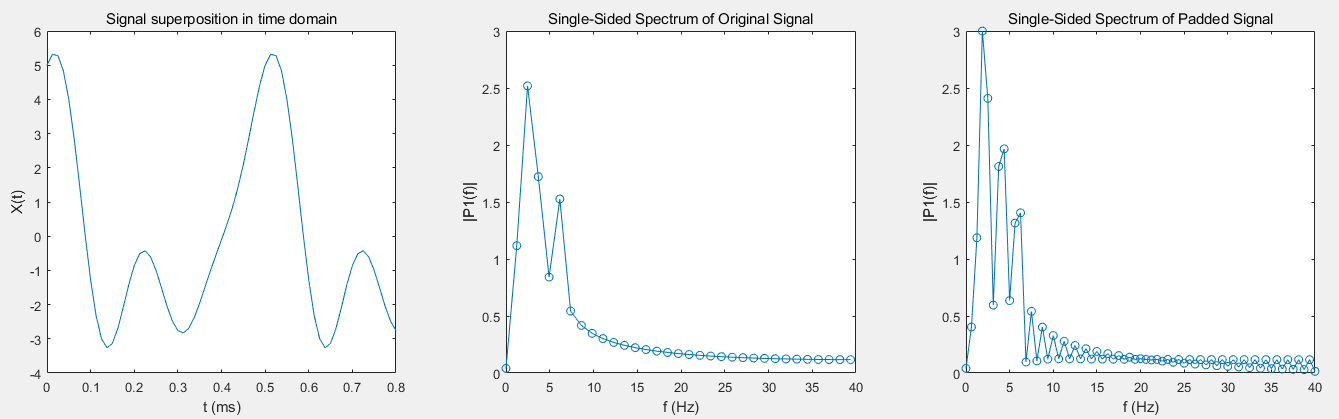
%在频域中绘制单侧频谱。由于信号的时间采样相当短，傅里叶变换的频率分辨率不够精确，不足以显示 4 Hz 附近的峰值频率。
subplot(132);
plot(f1,P1,"-o") 
title("Single-Sided Spectrum of Original Signal")
xlabel("f (Hz)")
ylabel("|P1(f)|")

%% 为了更好地评估峰值频率，您可以通过用零填充原始信号来增加分析窗的长度。这种方法以更精确的频率分辨率自动对信号的傅里叶变换进行插值。
%从原始信号长度确定是下一个 2 次幂的新输入长度。用尾随零填充信号 X 以扩展其长度。计算填零后的信号的傅里叶变换。
N = 2^nextpow2(L);
Y = fft(X,N);
%计算填零后的信号的单侧幅值频谱。由于信号长度 n 从 65 增加到 128，频率分辨率变为 Fs/n，即 0.625 Hz。

f2 = Fs*(0:(N/2))/N;
P4 = abs(Y/L);
P3 = P4(1:N/2+1);
P3(2:end-1) = 2*P3(2:end-1);
%绘制填零后的信号的单侧频谱。此新频谱在 0.625 Hz 的频率分辨率内显示 2 Hz、4 Hz 和 6 Hz 附近的峰值频率。
subplot(133);
plot(f2,P3,"-o") 
title("Single-Sided Spectrum of Padded Signal")
xlabel("f (Hz)")
ylabel("|P3(f)|")

填充零来对信号的傅里叶变换进行插值效果对比如下图：
在这里插入图片描述
需要注意的是：

1.由于进行fft点数的不同，将双边谱转换为单边谱的计算有所区别。如代码中25行以及43行所示。

2.补零后，频率分辨率由原来的Fs/L变为Fs/N,补零以后能改善栅栏效应，使原先不清晰的谱线显现。虽然数据长度在补零后增长到N，但其有效长度还应该是L，且计算幅值是要以有效长度来计算的。参看代码23行和41行。参看FFT中的补零问题_fft补零的效果更加明显。

双边谱转换为单边谱

解释如下(注意MATLAB中的向量索引从1开始，以下解释为0开始)：
假设序列{y}的DFT序列{Y}长度也为N，表示为：
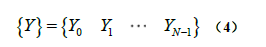
在这里插入图片描述
根据傅立叶变换的理论，这个序列中的后半部分实际上表示的是负频率信息。实序列的傅立叶变换的元素间存在共轭关系：
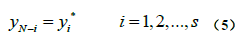
在这里插入图片描述
其中，常数s为：
img
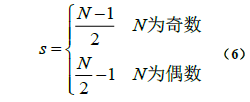
这样，当N是奇数时，可以将序列{Y}表示为：
img
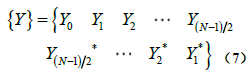
单边谱是长度为(N+1)/2的序列
img
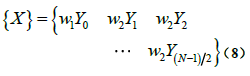
当N是偶数时，序列{Y}可以表示为：
img
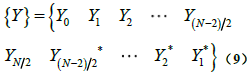
单边谱是长度为(N/2)+1的序列
img
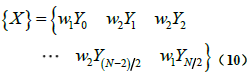
此处权系数取法是w1=1，w2=2。
具体参看：信号处理：单边、双边频谱间的相互转换

作者拙见，供参考：DFT序列Y0为直流分量，余下的序列存在共轭关系。点数N为奇数时，除去Y0，余下序列为偶数均能成对共轭，各占了一半，转换为单边谱时乘2；点数N为偶数时，除去Y0，余下序列为奇数，中间空下一个不能成对被共用，不必乘2，成对的转换为单边谱需要乘2。

如果 X 的长度大于 N，则对 X 进行截断以达到长度 N。

如果 n 小于信号的长度，则 fft 忽略第 n 个条目之后的其余信号值，并返回截断后的结果。
使用傅里叶变换求两种频率分量拼的信号,其中使用双边谱的绘制方式呈现频谱图。

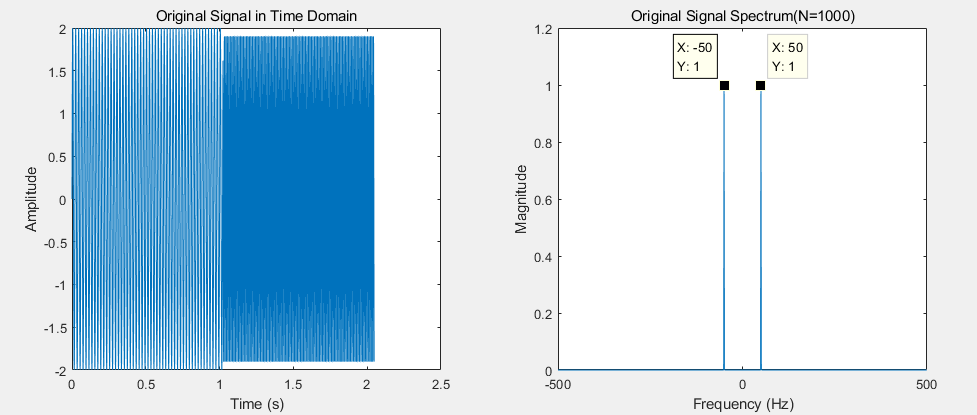
例：前1024个点为幅值为2，频率为50的信号；后1024个点为幅值为2，频率为100的信号；共2048个点。

fft(X,N)中的N取1000时可以看到频谱只有一个50的频率，由于是双边谱所以幅值各占一半。为什么只有一个频率啦，由于X信号的长度大于 N，所以将信号进行了截断，取前1000个点周期延拓求频谱。

clear all;close all;clc; %清理工作区，关闭所有窗口，清空文本

% 参数设置
fs = 1000;         % 采样率
f_signal1 = 50;    % 正弦信号频率1
f_signal2 = 100;    % 正弦信号频率2
t1 = 0:1/fs:(1024-1)/fs; 
t2 = 1024/fs:1/fs:(2048-1)/fs; 
% 生成正弦信号
signal1 = 2*sin(2*pi*f_signal1*t1);
signal2 = 2*sin(2*pi*f_signal2*t2);

%合并两不同频率信号 
t = [t1 t2];
signal = [signal1 signal2];

N = 1000;        %fft点数 
% 计算频率轴
fshift = (-N/2:N/2-1)*(fs/N);%注意范围
% 进行FFT
fft_signal =(abs(fft(signal,N)))/N;%此用法设置FFT点数为N
fft_signal_shift = fftshift(fft_signal);

% 绘制时域图和频谱图
figure(1);
% 时域图 - 原始信号
subplot(1, 2, 1);
plot(t, signal);
title('Original Signal in Time Domain');
xlabel('Time (s)');
ylabel('Amplitude');

% 频谱图 - 原始信号
subplot(1, 2, 2);
plot(fshift, fft_signal_shift);
title('Original Signal Spectrum');
xlabel('Frequency (Hz)');
ylabel('Magnitude');

N取1000时的时域和频谱图：
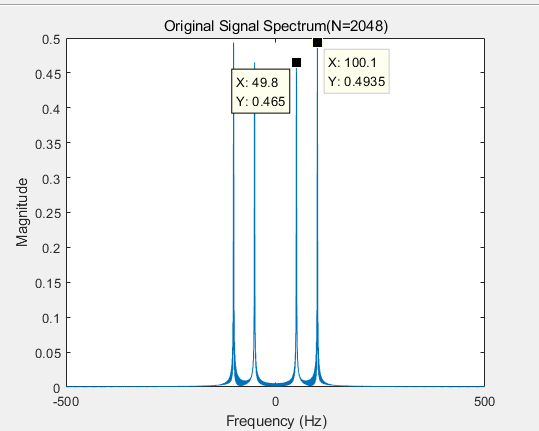
在这里插入图片描述
N取2048时的频谱图：
可以看出由于频率分辨率和截断(此处相当于加矩形窗)带来的频谱泄露的问题。此时出现两个频率分量。

在这里插入图片描述

语法三：Y = fft(X,N,dim)

dim — 沿其运算的维度 为正整数标量
沿其运算的维度，指定为正整数标量。如果不指定维度，则默认为第一个大于 1 的数组维度。

fft(X,[],1) 沿 X 的各列进行运算，并返回每列的傅里叶变换。
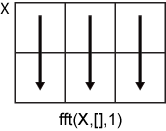
在这里插入图片描述
fft(X,[],2) 沿 X 的各行进行运算，并返回每行的傅里叶变换。
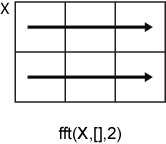
在这里插入图片描述
如果 dim 大于 ndims(X)，则 fft(X,[],dim) 返回 X。当指定 n 时，fft(X,n,dim) 将对 X 进行填充或截断，以使维度 dim 的长度为 n。

即dim=1，指定参数沿 X 的列使用 fft； dim =2 ，指定参数沿 X 的行使用 fft。(此处以dim =2 的行运算举例)：

clear all;close all;clc; %清理工作区，关闭所有窗口，清空文本
Fs = 1000;                    % Sampling frequency
T = 1/Fs;                     % Sampling period
L = 1000;                     % Length of signal
t = (0:L-1)*T;                % Time vector

%创建一个矩阵，其中每一行代表一个频率经过缩放的余弦波。结果 X 为 3×1000 矩阵。第一行的波频为 50，第二行的波频为 150，第三行的波频为 300。
x1 = cos(2*pi*50*t);          % First row wave
x2 = cos(2*pi*150*t);         % Second row wave
x3 = cos(2*pi*300*t);         % Third row wave

X = [x1; x2; x3];%X为3*1000double型

%在单个图窗中按顺序绘制 X 的每行的前 100 个项，并比较其频率。
figure(1);
for i = 1:3
    subplot(3,1,i)
    plot(t(1:100),X(i,1:100))
    title("Row " + num2str(i) + " in the Time Domain")
end

%指定 dim 参数沿 X 的行（即对每个信号）使用 fft。
dim = 2;
%计算信号的傅里叶变换。
Y = fft(X,L,dim);
%计算每个信号的双侧频谱和单侧频谱。
P2 = abs(Y/L);
P1 = P2(:,1:L/2+1);
P1(:,2:end-1) = 2*P1(:,2:end-1);

%在频域内，为单个图窗中的每一行绘制单侧幅值频谱。
figure(2);
for i=1:3
    subplot(3,1,i)
    plot(0:(Fs/L):(Fs/2-Fs/L),P1(i,1:L/2))
    title("Row " + num2str(i) + " in the Frequency Domain")
end

时域波形：
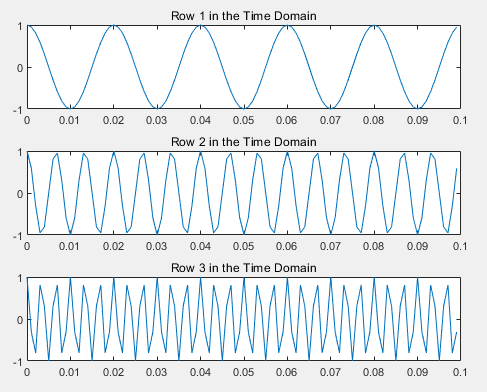
在这里插入图片描述
单边幅值频谱图：
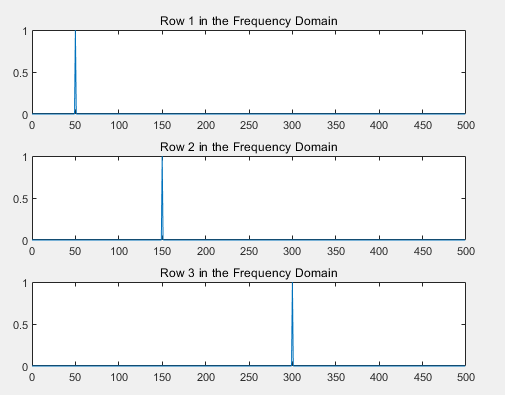
在这里插入图片描述

相位

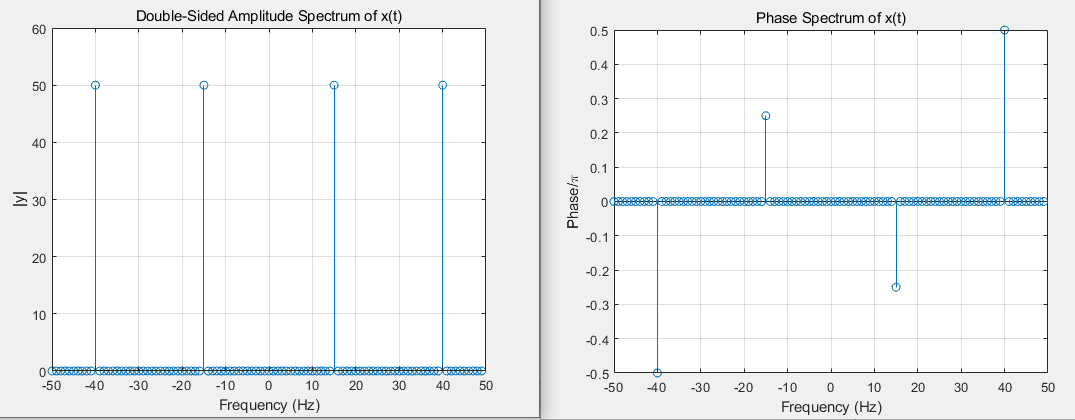
创建一个由频率为 15 Hz 和 40 Hz 的两个正弦波组成的信号。第一个正弦波是相位为 −π/4 的余弦波，第二个正弦波是相位为 π/2 的余弦波。以 100 Hz 的频率对信号进行 1 秒钟的采样。

clear all;close all;clc; %清理工作区，关闭所有窗口，清空文本
Fs = 100;
t = 0:1/Fs:1-1/Fs;
x = cos(2*pi*15*t - pi/4) + cos(2*pi*40*t + pi/2);

%计算信号的傅里叶变换。将变换幅值绘制为频率函数。
y = fft(x);
z = fftshift(y);
figure(1);
ly = length(y);
f = (-ly/2:ly/2-1)/ly*Fs;
stem(f,abs(z))
title("Double-Sided Amplitude Spectrum of x(t)")
xlabel("Frequency (Hz)")
ylabel("|y|")
grid

%计算变换的相位，删除小幅值变换值。将相位绘制为频率函数。
tol = 1e-6;
z(abs(z) < tol) = 0;%删除小幅值变换值

theta = angle(z);

figure(2);
stem(f,theta/pi)
title("Phase Spectrum of x(t)")
xlabel("Frequency (Hz)")
ylabel("Phase/\pi")
grid

幅度和相位谱：
在这里插入图片描述

补充

向量的离散傅里叶变换

Y = fft(X) 和 X = ifft(Y) 分别实现傅里叶变换和傅里叶逆变换。对于长度为 n 的 X 和 Y，这些变换定义如下：
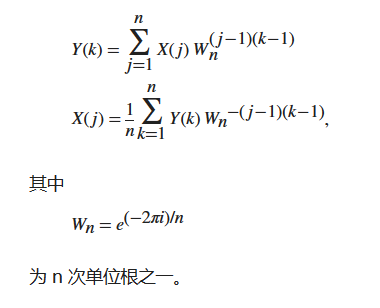
在这里插入图片描述

频谱泄露的解释

文章FFT中的补零问题_fft补零3.1 频谱泄漏仿真分析处及之后部分。

参考：

快速傅里叶变换 - MATLAB fft - MathWorks 中国

matlab信号频谱分析FFT详解_fft频谱图怎么看

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1259996.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

根据密码构成规则检测密码字符串

根据密码构成规则检测密码字符串

从键盘输入密码字符串&#xff0c;程序根据给定密码构成规则检测并给出对应提示。 (笔记模板由python脚本于2023年11月27日 19:27:47创建&#xff0c;本篇笔记适合熟悉Python字符串str对象的coder翻阅) 【学习的细节是欢悦的历程】 Python 官网&#xff1a;https://www.python.…
阅读更多...
ViLT 论文精读【论文精读】

ViLT 论文精读【论文精读】

ViLT 论文精读【论文精读】_哔哩哔哩_bilibili 目录 ViLT 论文精读【论文精读】_哔哩哔哩_bilibili 1 地位 2 ViLT做了什么能让它成为这种里程碑式的工作&#xff1f; 3 ViLT到底把模型简化到了什么程度&#xff1f;到底能加速到什么程度&#xff1f; 2.1 过去的方法是怎…
阅读更多...
C++之算术生成算法

C++之算术生成算法

C之算术生成算法 accumulate #include<iostream> using namespace std; #include<vector> #include<numeric>void test() {vector<int> v;for (int i 0; i < 10; i){v.push_back(i);}int total accumulate(v.begin(), v.end(),0);cout << t…
阅读更多...
论文公式工具

论文公式工具

论文公式工具 https://www.latexlive.com/home## 论文图片识别公式网页工具&#xff0c;免费的方便但是有限制次数&#xff0c;一天只能用三次公式图片识别。 先注册登录 我们到论文中截取一张图片 在识别得到的一串码中&#xff0c;删掉前面没用的 输出为这个格式&#x…
阅读更多...
从零构建属于自己的GPT系列1：预处理模块(逐行代码解读)、文本tokenizer化

从零构建属于自己的GPT系列1：预处理模块(逐行代码解读)、文本tokenizer化

1 训练数据 在本任务的训练数据中&#xff0c;我选择了金庸的15本小说&#xff0c;全部都是txt文件 数据打开后的样子 数据预处理需要做的事情就是使用huggingface的transformers包的tokenizer模块&#xff0c;将文本转化为token 最后生成的文件就是train_novel.pkl文件&a…
阅读更多...
【MATLAB】LMD分解+FFT+HHT组合算法

【MATLAB】LMD分解+FFT+HHT组合算法

有意向获取代码&#xff0c;请转文末观看代码获取方式~也可转原文链接获取~ 1 基本定义 LMDFFTHHT组合算法是一种基于局部均值分解&#xff08;LMD&#xff09;、快速傅里叶变换&#xff08;FFT&#xff09;和希尔伯特-黄变换&#xff08;HHT&#xff09;的组合算法。 LMD是…
阅读更多...
什么是数据增强，为什么会让模型更健壮？

什么是数据增强，为什么会让模型更健壮？

在做一些图像分类训练任务时&#xff0c;我们经常会遇到一个很尴尬的情况&#xff0c;那就是&#xff1a; 明明训练数据集中有很多可爱猫咪的照片&#xff0c;但是当我们给训练好的模型输入一张戴着头盔的猫咪进行测试时&#xff0c;模型就不认识了&#xff0c;或者说识别精度…
阅读更多...
87基于matlab的双卡尔曼滤波算法

87基于matlab的双卡尔曼滤波算法

基于matlab的双卡尔曼滤波算法。第一步使用了卡尔曼滤波算法&#xff0c;用电池电压来修正SOC&#xff0c;然后将修正后的SOC作为第二个卡尔曼滤波算法的输入&#xff0c;对安时积分法得到的SOC进行修正&#xff0c;最终得到双卡尔曼滤波算法SOC估计值。结合EKF算法和安时积分法…
阅读更多...
企业联系方式真的那么难获取吗？

企业联系方式真的那么难获取吗？

企业联系方式的重要性&#xff0c;相信每一个销售人员都是知道的。对于销售来说&#xff0c;获取准确、全面的企业联系方式&#xff0c;无疑是开发客户的基础与保障&#xff0c;任凭能力再高&#xff0c;说服能力多强&#xff0c;没有与客户接触的机会&#xff0c;这些都是无稽…
阅读更多...
CAN总线星型连接器及特点

CAN总线星型连接器及特点

CAN总线星型连接特点 CAN总线是一种广泛应用于汽车、工业自动化、家庭等领域的现场总线技术。它具有高速度、高可靠性、灵活性等特点&#xff0c;被广泛应用于汽车电子、工业自动化、家庭自动化等领域。在CAN总线的实际应用中&#xff0c;其连接方式可以是星型或菊花型。本文将…
阅读更多...
Pycharm在debug问题解决方案

Pycharm在debug问题解决方案

Pycharm在debug问题解决方案 前言一、Frames are not available二、查看变量时一直显示collecting data并显示不了任何内容 前言 Pycharm在debug时总是出现一些恼人的问题&#xff0c;以下是博主在训练中遇到的问题及在网上找到的可用解决方案&#xff1a; 一、Frames are not…
阅读更多...
自己动手写编译器:golex 和 flex 比较研究 2

自己动手写编译器:golex 和 flex 比较研究 2

上一节我们运行了 gcc 使用的词法解析器&#xff0c;使用它从.l 文件中生成对应的词法解析程序。同时我们用相同的词法规则对 golex 进行测试&#xff0c;发现 golex 同样能实现相同功能&#xff0c;当然这个过程我们也发现了 golex 代码中的不少 bug&#xff0c;本节我们继续对…
阅读更多...
基于单片机病房呼叫程序和仿真

基于单片机病房呼叫程序和仿真

如果学弟学妹们在毕设方面有任何问题&#xff0c;随时可以私信我咨询哦&#xff0c;有问必答&#xff01;学长专注于单片机相关的知识&#xff0c;可以解决单片机设计、嵌入式系统、编程和硬件等方面的难题。 愿毕业生有力&#xff0c;陪迷茫着前行&#xff01; 一、系统方案 1…
阅读更多...
程序员必读之软件架构书摘

程序员必读之软件架构书摘

程序员必读之软件架构书摘 什么是架构 "架构"作为名词的一种理解&#xff1a; 从产品整体考虑&#xff0c;采用一定的结构&#xff0c;将产品分解为一系列组件、模块和交互。 比如考虑处理软件的安全、配置、错误处理等横切关注点的基础设施服务。 "架构&q…
阅读更多...
广联达linkworks 文件上传漏洞复现

广联达linkworks 文件上传漏洞复现

0x01 产品简介 广联达 LinkWorks&#xff08;也称为 GlinkLink 或 GTP-LinkWorks&#xff09;是广联达公司&#xff08;Glodon&#xff09;开发的一种BIM&#xff08;建筑信息模型&#xff09;协同平台。广联达是中国领先的数字建造技术提供商之一&#xff0c;专注于为建筑、工…
阅读更多...
新手用什么工具制作电子画册？新分享

新手用什么工具制作电子画册？新分享

随着数字化时代的到来&#xff0c;电子画册已成为企业宣传、展示产品的重要手段。对于新手来说&#xff0c;选择一款合适的工具是关键。今天&#xff0c;为大家推荐一款适合新手制作的电子画册工具&#xff0c;让你轻松制作出精美画册。 工具推荐&#xff1a;FLBOOK在线制作电子…
阅读更多...
关于mybatis插入返回主键id和SpringBoot事务注解自调用演示

关于mybatis插入返回主键id和SpringBoot事务注解自调用演示

文章目录 一. 插入返回任意规则主键ID二. SpringBoot自调用事务2.1 场景12.2 场景2 自调用结论总结 一. 插入返回任意规则主键ID 实体对象 TableName("bank") Data public class Entity {TableId("id")Integer id;TableField("money")Integer …
阅读更多...
[原创][1]探究C#多线程开发细节-“Thread类的简单使用“

[原创][1]探究C#多线程开发细节-“Thread类的简单使用“

[简介] 常用网名: 猪头三 出生日期: 1981.XX.XXQQ: 643439947 个人网站: 80x86汇编小站 https://www.x86asm.org 编程生涯: 2001年~至今[共22年] 职业生涯: 20年 开发语言: C/C、80x86ASM、PHP、Perl、Objective-C、Object Pascal、C#、Python 开发工具: Visual Studio、Delphi…
阅读更多...
代码随想录算法训练营第五十七天|739. 每日温度、496.下一个更大元素 I

代码随想录算法训练营第五十七天|739. 每日温度、496.下一个更大元素 I

LeetCode 739. 每日温度 题目链接&#xff1a;739. 每日温度 - 力扣&#xff08;LeetCode&#xff09; 单调栈开始&#xff0c;为什么要用栈&#xff0c;因为栈是先入后出&#xff0c;当我们遍历从前往后的时候&#xff0c;每次遍历的元素都是添加至栈尾&#xff0c;方便我们进…
阅读更多...
勒索解密后oracle无法启动故障处理----惜分飞

勒索解密后oracle无法启动故障处理----惜分飞

客户linux平台被勒索病毒加密,其中有oracle数据库.客户联系黑客进行解密【勒索解密oracle失败】,但是数据库无法正常启动,dbv检查数据库文件报错 [oraclehisdb ~]$ dbv filesystem01.dbf DBVERIFY: Release 11.2.0.1.0 - Production on 星期一 11月 27 21:49:17 2023 Copyrig…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023