对于下面的内容,大家着重观察和理解图即可,可以直接绕过一些文字性的概念,对图有一个大概的认识。
图
- 简单认识图
- 图的定义
- 有向图和无向图
- 完全图
- 无向完全图
- 有向完全图
- 图的基本存储结构
- 邻接矩阵存储
- 邻接矩阵的优点
- 网络的邻接矩阵
- 邻接表
- 无向图的邻接表
- 有向图的邻接表
- 关于顶点的度、出度与入度
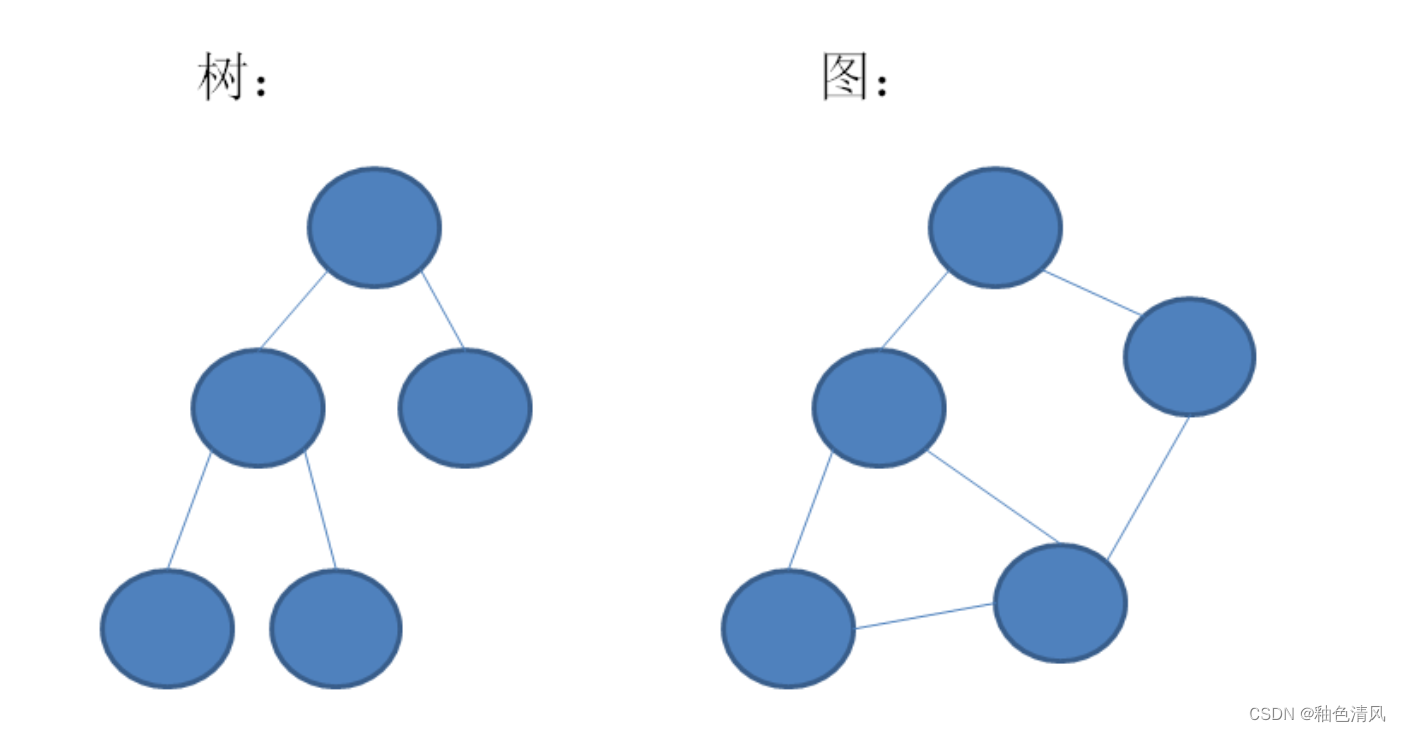
简单认识图
图,是一种比树更为复杂的数据结构。树的节点之间是一对多的关系,并且存在父与子的层级划分;而图的顶点(注意,这里不叫节点)之间是多对多的关系,并且所有顶点都是平等的,无所谓谁是父谁是子。
图的定义
图 是由一个非空的顶点集合和一个描述顶点之间多对多关系的边(或弧)集合组成的一种数据结构,它可以形式化地表示为: 图=(V,E
其中V={x|x∈某个数据对象集},它是顶点的有穷非空集合;E={(x,y)|x,y∈V}或E={<x,y>|x,y∈V且P(x,y)},它是顶点之间关系的有穷集合,也叫做边集合,P(x,y)表示从x到y的一条单向通路。
有向图和无向图
若图G中的每条边都是有方向的,则称G为有向图。在有向图中,一条有向边是由两个顶点组成的有序对,有序对通常用尖括号表示。例如,有序对<vi,vj>表示一条由vi到vj的有向边。有向边又称为弧,弧的始点称为弧尾,弧的终点称为弧头。若图G中的每条边都是没有方向的,则称G为无向图。无向图中的边均是顶点的无序对,无序对通常用圆括号表示。
下面我们举例说明:
①如下图所示,顶点集合V(G1)={
V
0
,
V
1
,
V
2
,
V
3
,
V
4
V_0,V_1,V_2,V_3,V_4
V0,V1,V2,V3,V4}
边集合为E(G1)={
(
V
0
,
V
1
)
,
(
V
0
,
V
3
)
,
(
V
1
,
V
2
)
,
(
V
1
,
V
4
)
,
(
V
2
,
V
3
)
,
(
V
2
,
V
4
)
(V_0,V_1),(V_0,V_3),(V_1,V_2),(V_1,V_4),(V_2,V_3),(V_2,V_4)
(V0,V1),(V0,V3),(V1,V2),(V1,V4),(V2,V3),(V2,V4)} 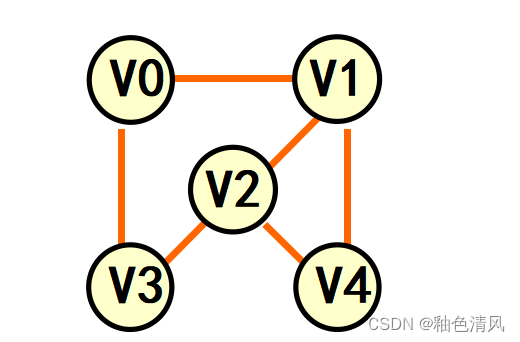
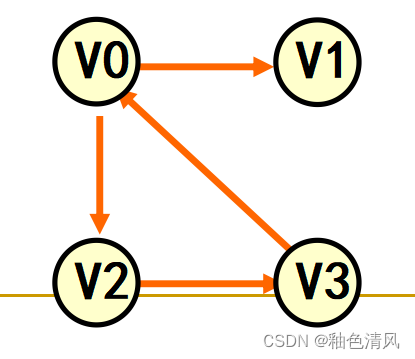
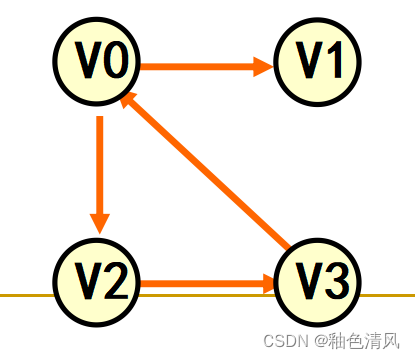
②如下图所示,顶点集合V(G2)={
V
0
,
V
1
,
V
2
,
V
3
V_0,V_1,V_2,V_3
V0,V1,V2,V3}
边集合为E(G2)={
<
V
0
,
V
1
>
,
<
V
0
,
V
2
>
,
<
V
2
,
V
3
>
,
<
V
3
,
V
0
>
<V_0,V_1>,<V_0,V_2>,<V_2,V_3>,<V_3,V_0>
<V0,V1>,<V0,V2>,<V2,V3>,<V3,V0>}

完全图
简单来说,完全图具有最多的边数,任意一对顶点间均有边相连。
无向完全图
对于具有n个顶点的完全图,如果每两个顶点之间都有相连,也就是边数为
e=
(
n
−
1
)
+
(
n
−
2
)
+
.
.
.
+
1
(n-1)+(n-2)+...+1
(n−1)+(n−2)+...+1=
n
(
n
−
1
)
2
\frac{n(n-1)}{2}
2n(n−1),就是完全图,否则,就是不完全图。
如下图所示,即为无向完全图。
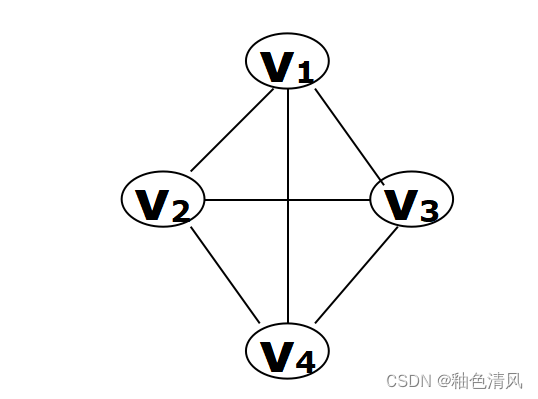
有向完全图
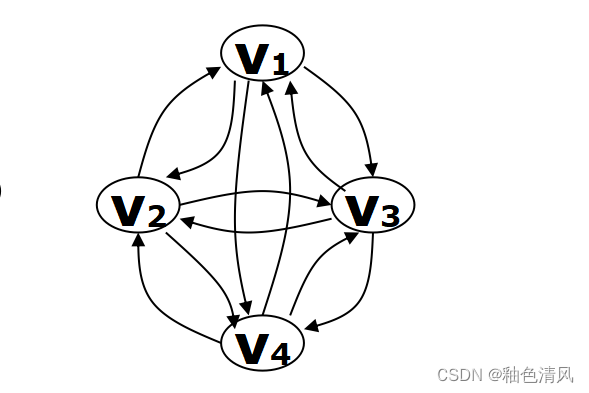
对于具有n个顶点的完全图,如果每两个顶点之间都有相连,也就是边数为n(n-1),那么即为有向完全图。
如下图所示,即为有向完全图。
图的基本存储结构
图的存储结构至少要保存两类信息:
1)顶点的数据
2)顶点间的关系
邻接矩阵存储
给定图G=(V,E),其中V(G)={v0,…,vi,…,vn-1},G的邻接矩阵(Adacency Matrix)是具有如下性质的n阶方阵:

下面,我们举例说明:
写出如下两个图的邻接矩阵。
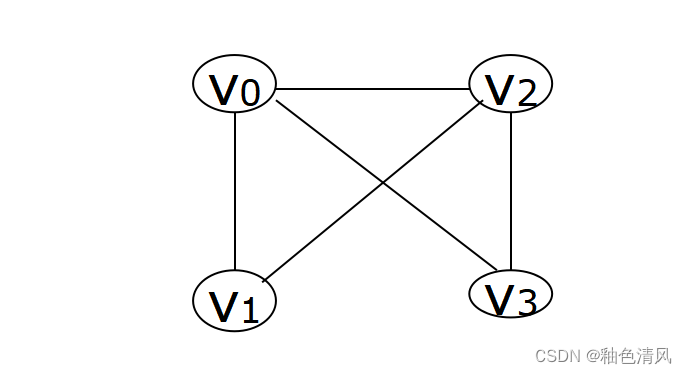
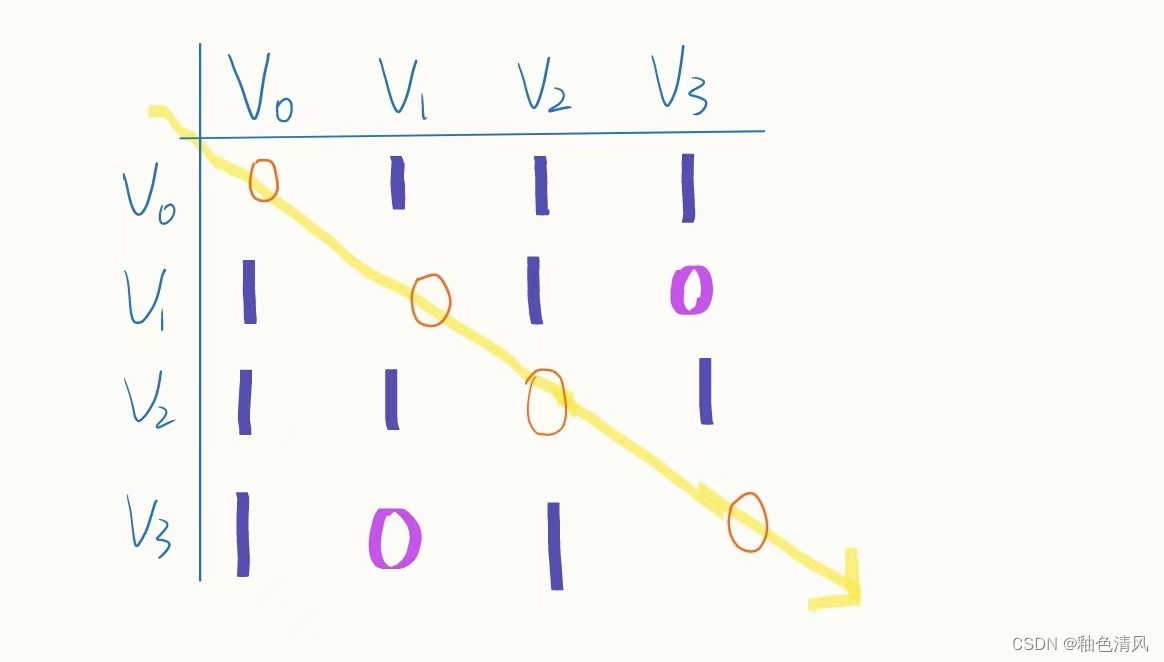
所以它的邻接矩阵为:
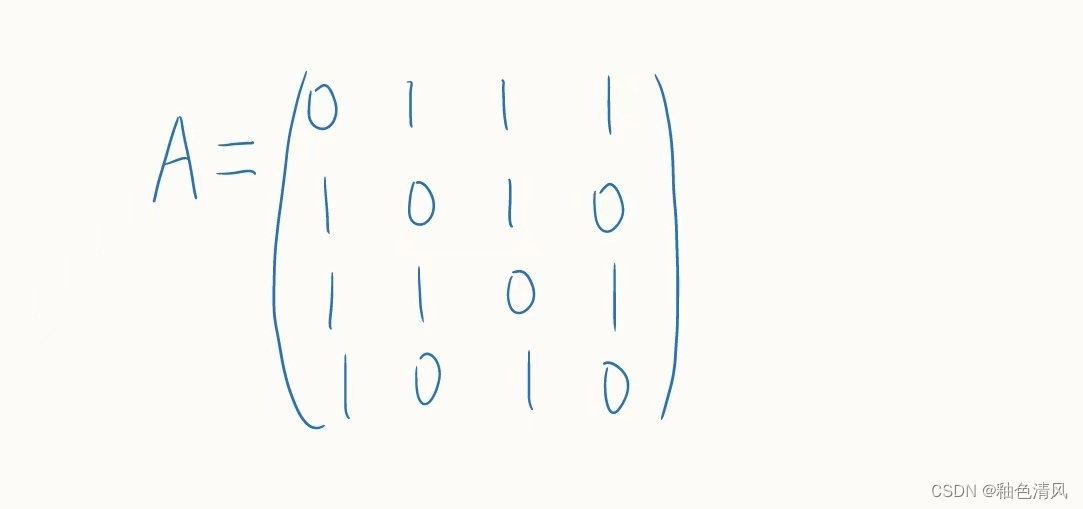
我们可以观察得知,无向图的邻接矩阵是对称的,有向图的邻接矩阵可能是不对称的。
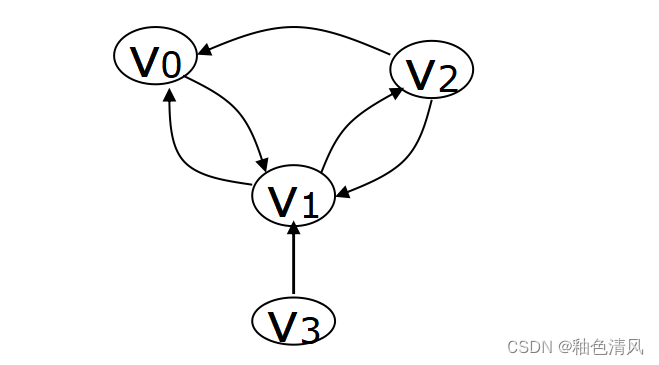

所以它的邻接矩阵为:

邻接矩阵的优点
邻接矩阵的优点在于用邻接矩阵表示图,很容易判定任意两个顶点之间是否有边相连,并求得各个顶点的度数。
对于无向图,顶点vi的度数是邻接矩阵中第i行或第i列值为1的元素个数。
对于有向图,邻接矩阵中第i行值为1的元素个数为顶点vi的出度,第i列值为1的元素的个数为顶点vi的入度。
网络的邻接矩阵
当G=(V,E)是一个网络时,G的邻接矩阵是具有如下性质的n阶方阵:

其中Wij表示边上的权值;∞表示一个计算机允许的、大于所有边上权值的数。
下面我们举例说明:
①对于如下这个无向图,求邻接矩阵
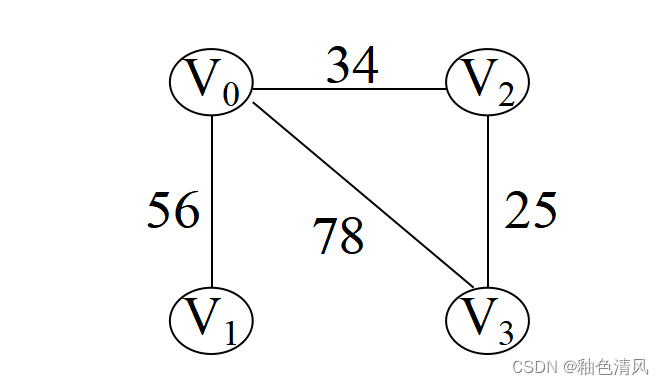
它的邻接矩阵为:

②对于如下这个有向图,求邻接矩阵
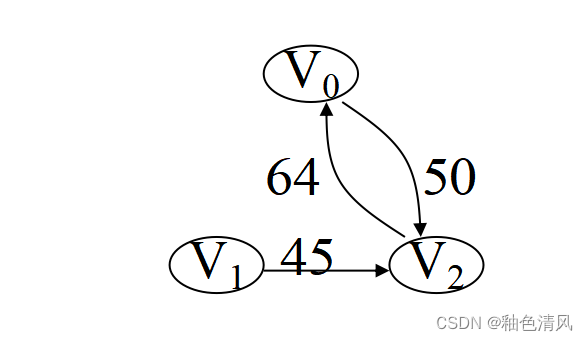
它的邻接矩阵为:
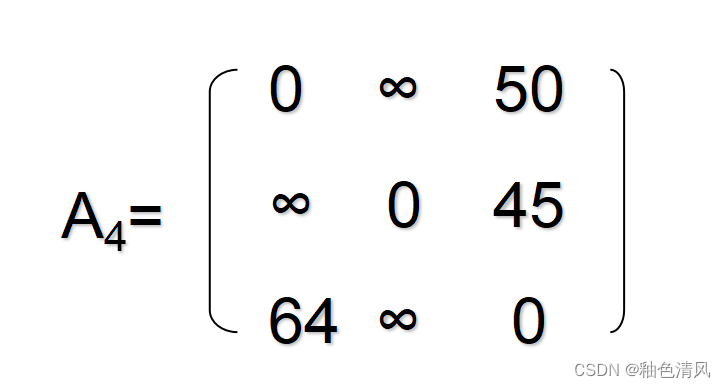
邻接表
如上可以知道,邻接矩阵可以直观地看出一个顶点和另一个顶点之间的关联关系。
但是,邻接矩阵的缺点时什么呢?就是占用太多空间了。
举个例子来说,如果有100个顶点,这100个顶点之间只有10个顶点之间有关联关系,那么就需要建立一个100×100的矩阵,在这个邻接矩阵中,就只有10或20个1,其余都是0,这样的矩阵也叫做 稀疏矩阵,太浪费存储空间了。
所以,为了解决邻接矩阵占用空间的问题,人们想到了另一中种图的表示方法:邻接表。
无向图的邻接表
对于图G中的每个顶点vi,该方法把所有邻接于vi的顶点vj链成一个带头结点的单链表,这个单链表就称为顶点vi的邻接表。
单链表中的每个结点至少包含两个域,一个为邻接点域(adjvex),它指示与顶点vi邻接的顶点在图中的位序,另一个为链域(next),它指示与顶点vi邻接的下一个结点。
如下图所示:
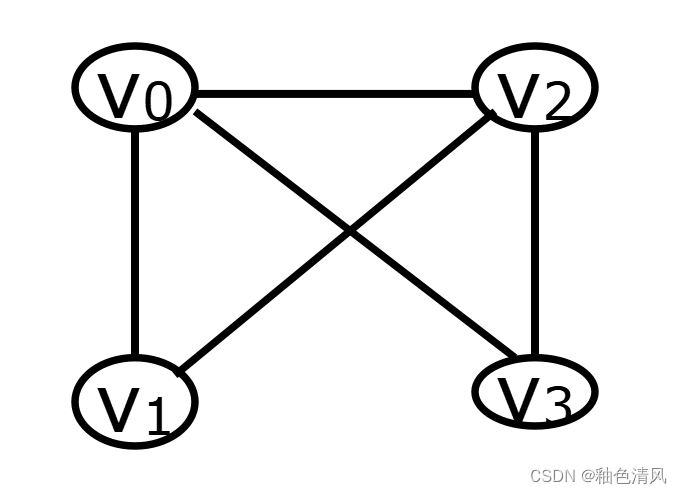
简单理解单链表的组成:
其实,可以将图的单链表理解成由一个又一个“带头结点的单链表”组成的。
当然,严谨来说,肯定不是单链表。这是因为它的表头结点结构和边表结点的结构不同。

它的邻接表为:
有向图的邻接表
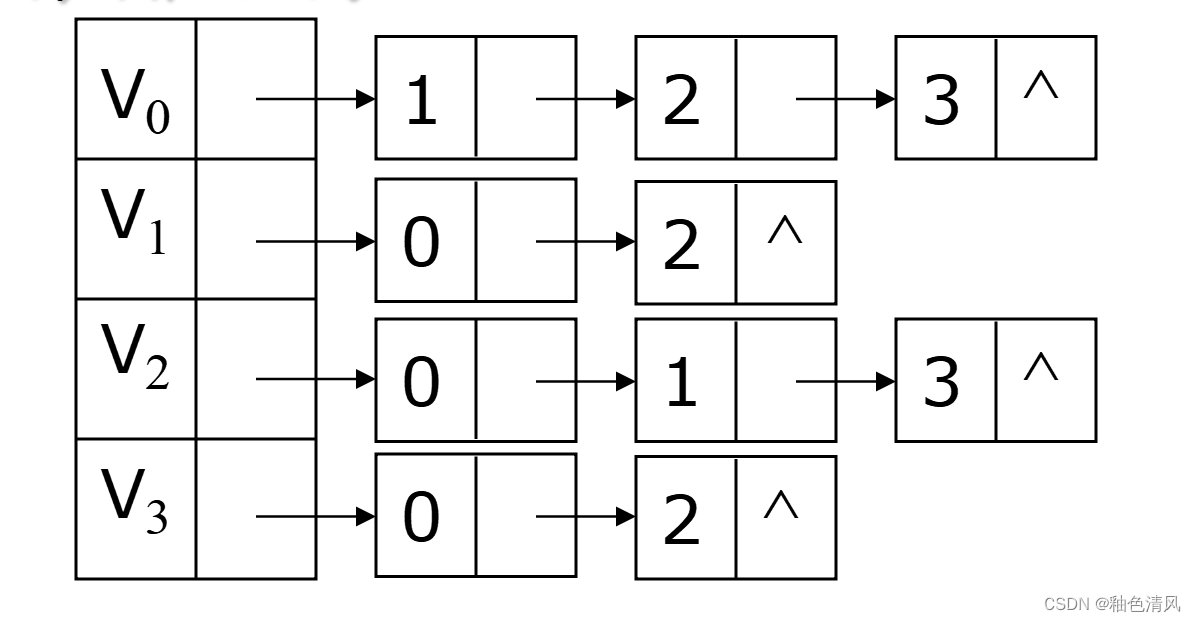
对于有向图来说,如果每一顶点vi的邻接表中每个表结点都存储以vi的为始点射出的一条边,则称这种表为有向图的出边表(有向图的邻接表),反之,若每一顶点vi的邻接表中每个表结点都对应于以vi为终点的边(即射入vi的边),则称这种表为有向图的入边表(又称逆邻接表)。
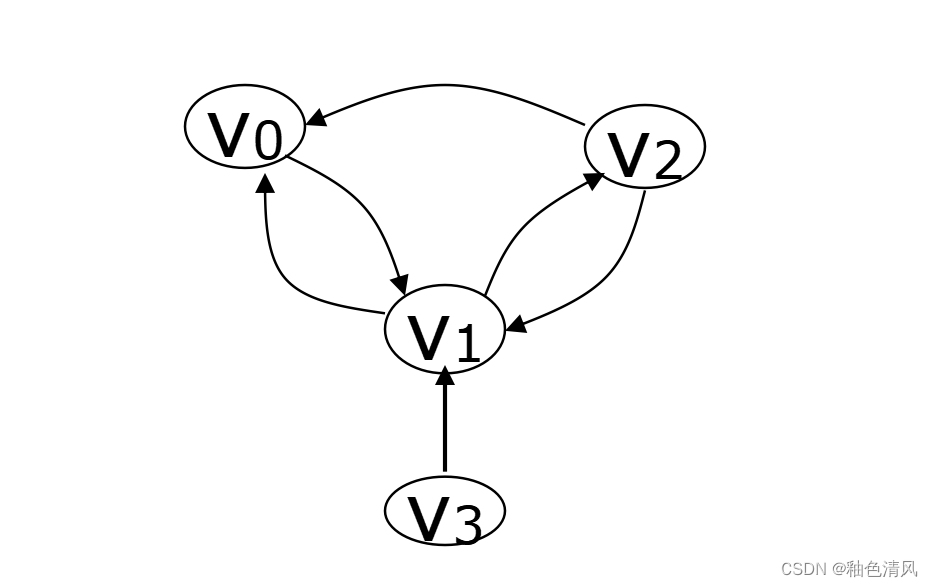
举例如下图所示:
它的出边表:

关于顶点的度、出度与入度
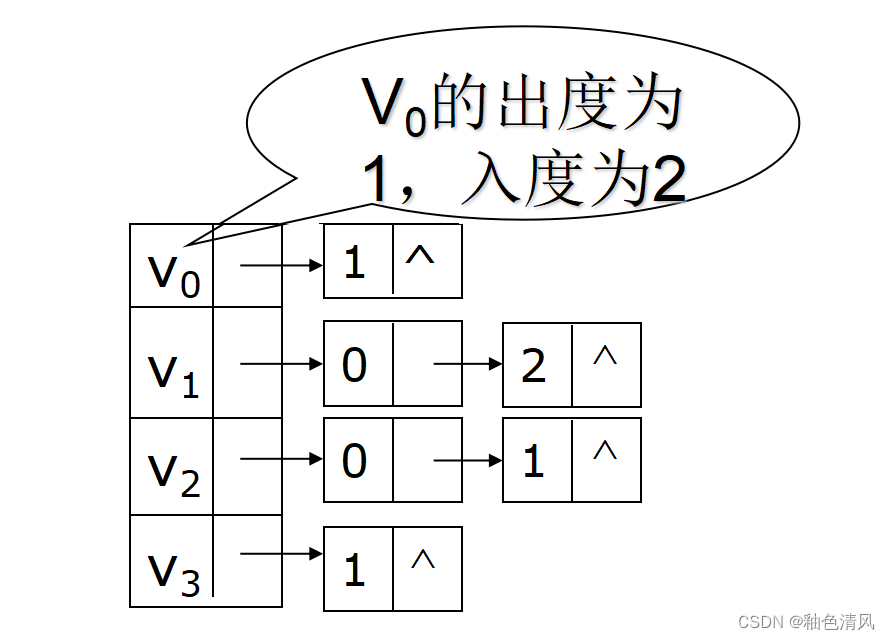
在无向图的邻接表中,顶点vi的度为第i个链表中结点的个数;而在有向图的出边表中,第i个链表中的结点个数是顶点vi的出度;为了求入度,必须对整个邻接表扫描一遍,所有链表中其邻接点域的值为i的结点的个数是顶点vi的入度。
若如下图所示已知该图是无向图,则可知,改图种V0的度为3.

若如下图所示,已知改图是有向图,则可知 V0的出度为1,V0的入度为2。