leetcode刷题详解六

124. 二叉树中的最大路径和

这个解析很好

所有树的题目，都想成一颗只有根、左节点、右节点的小树。然后一颗颗小树构成整棵大树，所以只需要考虑这颗小树即可。接下来分情况，按照题意：一颗三个节点的小树的结果只可能有如下6种情况：

根 + 左 + 右
根 + 左
根 + 右
根
左
右

只有 2,3,4 可以向上累加，而1,5,6不可以累加（这个很好想，情况1向上累加的话，必然出现分叉，情况5和6直接就跟上面的树枝断开的，没法累加），所以我们找一个全局变量存储 1,5,6这三种不可累加的最大值，另一方面咱们用遍历树的方法求2,3,4这三种可以累加的情况。最后把两类情况得到的最大值再取一个最大值即可。

class Solution {
public:
    int case1 = INT_MIN;
    int maxPathSum(TreeNode* root) {
        int case2 = dfs(root);
        return max(case1, case2);
    }
    int dfs(TreeNode* root){
        if(!root){
            //注意，不能return0，-3这个例子就出粗哦了
            //因为节点会比0更小
            return -1000;
        }
        int left = dfs(root->left);
        int right = dfs(root->right);
        //一下三种情况无法回溯给父节点收益，所以只能全局变量Case1记录一下。
        case1 = max(root->val + left + right, case1);
        case1 = max(case1, left);
        case1 = max(case1, right);
        int case2 = root->val;
        case2 = max(case2, root->val + left);
        case2 = max(case2, root->val + right);
        return case2;
    }
};

236. 二叉树的最近公共祖先

详细解释

TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
    if(!root || root == q || root == p){
        return root;
    }
    TreeNode* left = lowestCommonAncestor(root->left, p, q);
    TreeNode* right = lowestCommonAncestor(root->right, p, q);
    if(!left){
        return right;
    }
    if(!right){
        return left;
    }
    if(!left && !right){
        return nullptr;
    }
    return root;
}

102. 二叉树的层序遍历

思路：本质上还是层序遍历，只不过要循环一下每一层的节点数而已

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int>> result;
        queue<TreeNode* > m_queue;
        if(root){
            m_queue.push(root);
        }
        while(!m_queue.empty()){
            int len = m_queue.size();
            vector<int> rec;
            for(int i = 0; i < len; i++){
                TreeNode* tmp = m_queue.front();
                rec.push_back(tmp->val);
                m_queue.pop();
                if(tmp->left){
                    m_queue.push(tmp->left);
                }
                if(tmp->right){
                    m_queue.push(tmp->right);
                }
            }
            result.push_back(rec);
        }
        return result;
    }
};

222. Count Complete Tree Nodes

这个题就是完全二叉树的性质，给一个二叉树，然后判断有几个节点，下图很能说明情况：

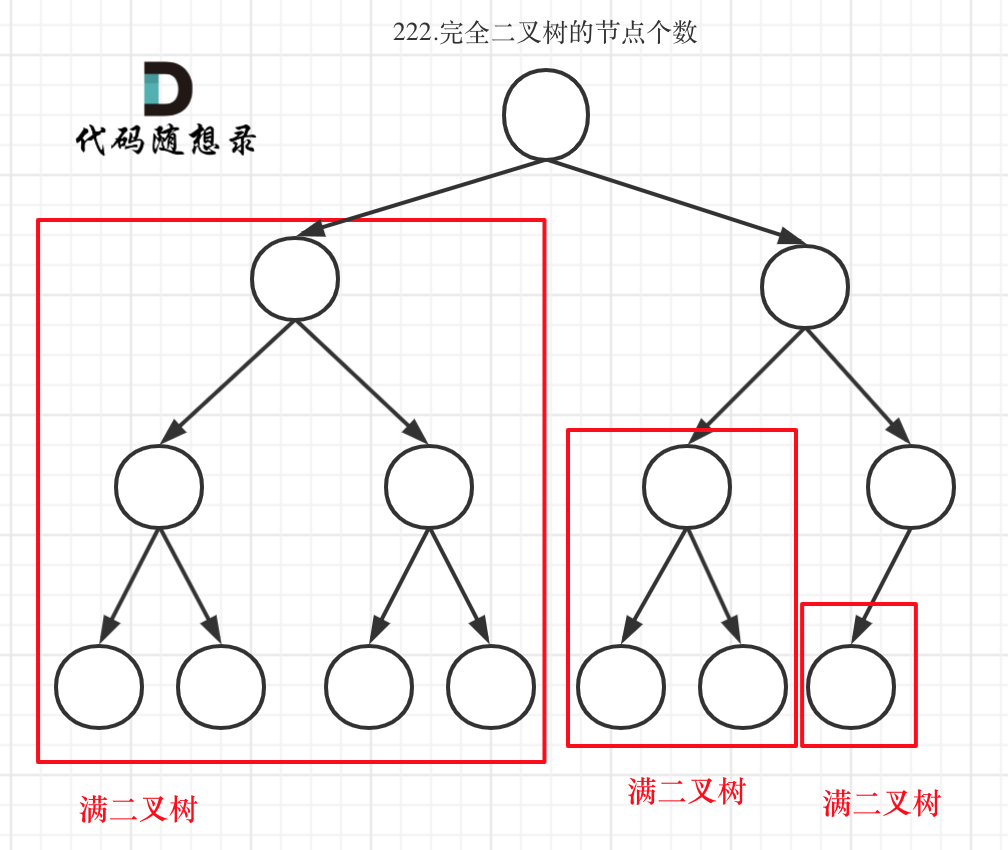
如果是满二叉树，直接就是 $2^n-1$ ，如果不是满二叉树，那么就往下递归呗

int countNodes(TreeNode* root) {
    if(!root){
        return 0;
    }
    int left_height = 0;
    int right_height = 0;
    TreeNode* left_node = root->left;
    TreeNode* right_node = root->right;
    while(left_node){
        left_node = left_node->left;
        left_height++;
    }
    while(right_node){
        right_node = right_node->right;
        right_height++;
    }
    if(left_height == right_height){
        return (2<<left_height) - 1;
    }
    return countNodes(root->left) + countNodes(root->right) + 1; //1是根节点
}

二叉搜索树BST

700. 二叉搜索树中的搜索

TreeNode* searchBST(TreeNode* root, int val) {
        if(!root){
            return nullptr;
        }
        if(root->val == val){
            return root;
        }
        else if(root->val < val){
            return searchBST(root->right,val);
        }
        else if(root->val > val){
            return searchBST(root->left,val);
        }
        return nullptr;
    }

知识点

递归返回函数名称有什么需要注意的？

数据结构

BST数增山查改由于本身性质的原因，和普通二叉树肯定不一样。

因此本身是有框架的，如下

void BST(TreeNode root, int target) {    
    if (root.val == target)        // 找到目标，做点什么    
        if (root.val < target)         
            BST(root.right, target);    
    if (root.val > target)       
        BST(root.left, target);
}

230. 二叉搜索树中第K小的元素

这题是BST（二叉搜索树）

思路一： BST中序遍历就是升序排序，因此可以用中序遍历做，但是时间复杂度是O(n)，有点大，不太行

思路二：参考链接，题目中给定的数据结构无法实现思路二

vector<int> vec;
    int kthSmallest(TreeNode* root, int k) {
        reverse_tree(root);
        return vec[k-1];
    }
    void reverse_tree(TreeNode* root){
        if(!root){
            return ;
        }
        reverse_tree(root->left);
        vec.push_back(root->val);
        reverse_tree(root->right);
        return ;
    }

题目细节

由于原函数返回值是int，不适合递归，因此需要重新新一个辅助函数来完成树的递归。
涉及的数据结构
- BST（二叉搜索树）是一个有序的基础树，avl、rb_tree是在其基础上而来的，是自平衡的树，提供logN级别的增山查改效率
- BST树的特点：
  1. 对于 BST 的每一个节点node，左子树节点的值都比node的值要小，右子树节点的值都比node的值大。
  2. 对于 BST 的每一个节点node，左子树节点的值都比node的值要小，右子树节点的值都比node的值大。
- BST树中序遍历就是升序排序。

538. 把二叉搜索树转换为累加树

这道题真的真的特别的巧！！！！！

本质上还是二叉树的中序遍历，但是正常是升序。

我们需要逆序的节点顺序，因此先右后左不就行了！

int sum = 0;
TreeNode* convertBST(TreeNode* root) {
    if(!root){
        return nullptr;
    }
    convertBST(root->right);
    root->val = sum + root->val;
    sum = root->val;
    convertBST(root->left);
}

这道题就是巧！没别的！

98. 验证二叉搜索树

思路一：中序遍历是升序，别忘了！

思路二：递归，每一个根节点左子树也是BST，右子树也是BST

思路二有坑，主要在于对于每一个节点root，我们可能会写成判断root节点的左节点小于和右节点大于。这是错误的，因为BST树保证了必须是左节点为根节点的数也是BST，右节点同理

思路一代码：

long long temp = (long long)INT_MIN-1;
    bool isValidBST(TreeNode* root) {
        if(!root){
            return true;
        }
        if(!isValidBST(root->left)){
         return false;   
        }
        if(temp >= root->val){
            return false;
        }
        temp = root->val;
        if(!isValidBST(root->right)){
            return false;   
        }
        return true;
    }

上述代码可能不好理解，换一种写法，

long long temp = (long long)INT_MIN-1;
    bool isValidBST(TreeNode* root) {
        if(!root){
            return true;
        }
        bool left =  isValidBST(root->left);
        if(temp >= root->val){
            return false;
        }
        temp = root->val;
        bool right =  isValidBST(root->right);
        return left && right;
    }

本题需要注意的点
- 老生常谈的问题，在做递归的时候return不知道该怎么写。这道题函数的返回值是布尔类型，所以你也要写布尔类型的返回值，但是如何return就是一门学问了！
- 注意看代码long long temp = (long long)INT_MIN-1;
  
  这样写是因为有一个测试用例，[-2147483648] 这个值就是INT_MIN所以，我们最小值必须使用比INT_MIN小的才行，所以int越界了，就用long long ，不要忘记强制转换！

701. 二叉搜索树中的插入操作

TreeNode* insertIntoBST(TreeNode* root, int val) {
        if(!root){
            //二叉查找树肯定是放在根节点上！！！
            return new TreeNode(val);
        }
        if(root->val < val){
            root->right = insertIntoBST(root->right, val);
        }
        else if(root->val > val){
            root->left = insertIntoBST(root->left, val);
        }
        return root;
    }

450. 删除二叉搜索树中的节点

第二次写这道题的时候必须记录一下：在二叉树的递归中，如果你需要一个dummy节点，那么这个dummy节点其实就在root->left = delete(root->left)中，此时这个root就是前置节点！！！这一点一定要记好了！！

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* deleteNode(TreeNode* root, int key) {
        if(!root){
            return nullptr;
        }
        if(root->val == key){
            if(!root->left && !root->right){
                return nullptr;
            }
            else if(!root->left){
                return root->right;
            }
            else if(!root->right){
                return root->left;
            }else{
                TreeNode* tmp  = root->right;
                TreeNode* dummy = root;
                while(tmp->left){
                    dummy = tmp;
                    tmp = tmp->left;
                }
                cout<<"dummy->val"<<dummy->val<<endl;
                cout<<"tmp->val"<<tmp->val<<endl;
                root->val = tmp->val;
                //这点容易错 草他妈，要判断dummy是不是原来的节点
                if(dummy == root){
                    dummy->right = tmp->right;
                }
                else if(dummy != root){
                   dummy->left = tmp->right;
                }
            }
        }
        if(root->val > key){
            root->left = deleteNode(root->left, key);
        }
        if(root->val < key){
            root->right = deleteNode(root->right, key);
        }
        return root;
    }
};

涉及到的数据结构

这道题主要涉及二叉搜索树BST的删除问题。这个问题我想了三个小时，难点在于节点的删除的代码上

BST节点删除要分成三种情况
- 第一种
  
  当被删除的节点是叶子节点，即无左孩子也无右孩子时，直接删除即可，简单
- 第二种
  
  当被删除的节点只包含左孩子或者右孩子时，删除也很简单
- 第三种
  
  当被删除的节点同时包含左孩子或者右孩子。我们从被删除节点的右节点为起点，往左子树上找最后一个节点，画个图就知道了。
  
  然后把这个几点的值和被删除节点的互换，把该节点删掉就行。

96. 不同的二叉搜索树

举个例子，比如给算法输入n = 5，也就是说用{1,2,3,4,5}这些数字去构造 BST。

根据 BST 的特性，根节点的左子树都比根节点的值小，右子树的值都比根节点的值大。

所以如果固定3作为根节点，左子树节点就是{1,2}的组合，右子树就是{4,5}的组合。

左子树的组合数和右子树的组合数乘积就是3作为根节点时的 BST 个数。

这道题动态规划和递归都能写

动态规划

int numTrees(int n) {
       vector<int> vec(n+1, 0);
       vec[0] = 1;
       vec[1] = 1;
       for(int i = 2; i < n + 1; i++){
           for(int j = 1; j <= i; j++){
                vec[i] += vec[j - 1] * vec[i - j]; 
           }
           cout<<vec[i]<<endl;
       }
       return  vec[n];
    }

注意，当有0个数的时候，可以构成一个BST，因为空树也是！！！！