综述
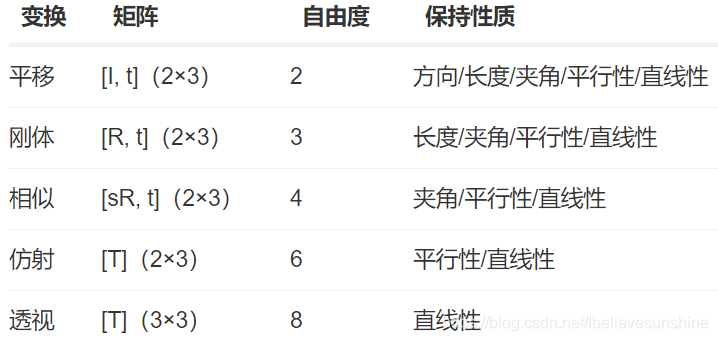
所有复杂的东西,都是由基本的组成的。所以我们需要先了解一下基础的变换有哪些:

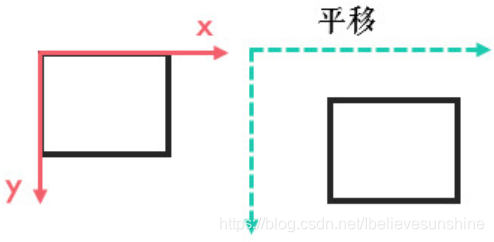
平移
我们对矩形(图像)平移,需要怎么做?
对每一个像素点坐标平移。可以让每一个像素点的x,y坐标都加一个变量。
矩阵形式表示:

等式左边[X,Y,1]是像素坐标的齐次形式。等式右边是平移之后的坐标。
放缩
进行放缩,就是将矩形(图像)放缩n倍,也就是长宽各乘一个变量。

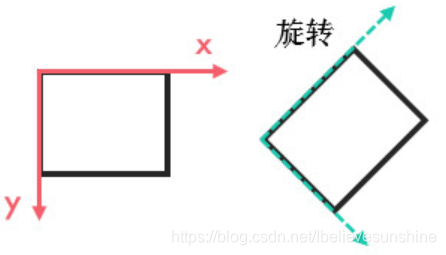
旋转
对矩形(图片)进行旋转,关于旋转的数学推导在后面仿射会介绍:

错切
前面的都比较直观,那错切是什么呢?
我们可以看下矩形关于y方向的错切:

看图就很直观了,那数学表达呢?

x轴上的错切就是同理了,公式如下:

然后两者和起来,就如下了:

好了,到此我们就了解了这四种变换了,那仿射变换是什么呢?可以看下图公式:

等式右边就是仿射变换矩阵,是由原图像平移,旋转,放缩,错切之后得来的。
在书上往往将仿射变换和透视变换放一起讲,这两者各是什么呢?
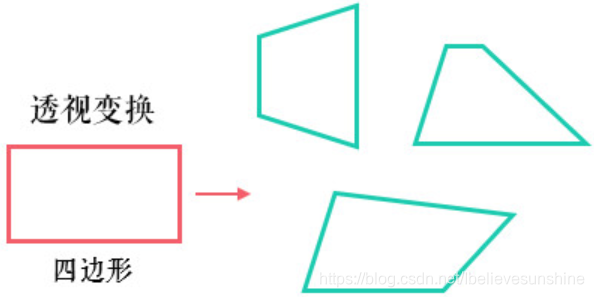
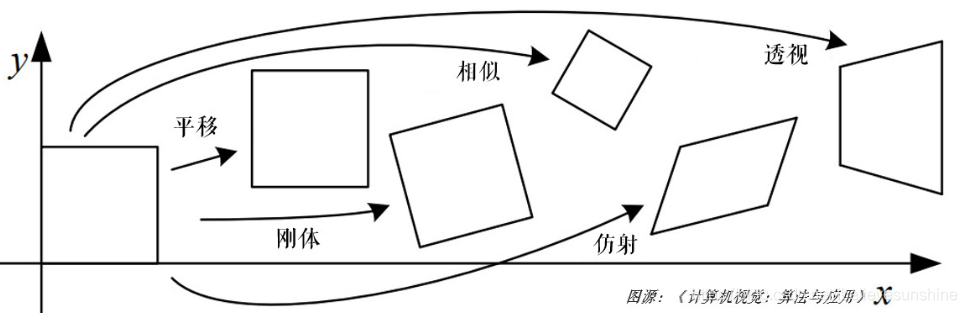
在刚学仿射变换和透视变换时,我是有些分不清的。印象最深刻的就是下图:

可以看到,仿射变换(下)是将矩形变换成平行四边形(即变换后各边依旧平行),而透视变换(上)可以变换成任意不规则四边形。
这样看来,好像仿射变换是透视变换的子集。
那到底是不是呢?其实是的。仿射变换属于线性变换,而透视变换则不仅仅是线性变换。仿射变换可以看做是透视变换的一种特例。
直观上感受,我们可以认为:
仿射变换是单纯对图片进行缩放,倾斜和旋转,因此图片不论如何变化,线之间的平行性是不变的。如下图。

可以感受到,右图是可以通过左图平移,旋转,错切,缩放之后得来。
而透视变换,则是当观察者的视角发生变化时物体发生的透视变换,此转换允许造成透视形变。
我们看下图的公路,近处宽远处窄,就是因为视角的原因,

仿射变换
原理
基本的图像变换就是二维坐标的变换:从一种二维坐标(x,y)到另一种二维坐标(u,v)的线性变换:
如果写成矩阵的形式,就是:
作如下定义:
矩阵T(2×3)就称为仿射变换的变换矩阵,R为线性变换矩阵,t为平移矩阵,简单来说,仿射变换就是线性变换+平移。变换后直线依然是直线,平行线依然是平行线,直线间的相对位置关系不变,因此非共线的三个对应点便可确定唯一的一个仿射变换,线性变换4个自由度+平移2个自由度→仿射变换自由度为6。
opencv中实现仿射变换
import cv2 as cv
import numpy as np
import matplotlib.pyplot as plt
img = cv.imread('drawing.jpg')
rows, cols = img.shape[:2]
# 变换前的三个点
pts1 = np.float32([[50, 65], [150, 65], [210, 210]])
# 变换后的三个点
pts2 = np.float32([[50, 100], [150, 65], [100, 250]])
# 生成变换矩阵
M = cv.getAffineTransform(pts1, pts2)
# 第三个参数为dst的大小
dst = cv.warpAffine(img, M, (cols, rows))
plt.subplot(121), plt.imshow(img), plt.title('input')
plt.subplot(122), plt.imshow(dst), plt.title('output')
plt.show()
实验结果
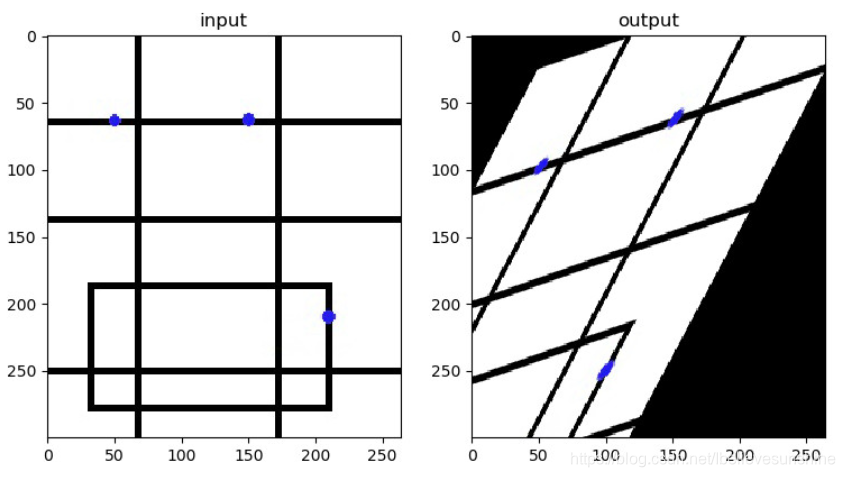
平移
平移就是x和y方向上的直接移动,可以上下/左右移动,自由度为2,变换矩阵可以表示为:
旋转
旋转是坐标轴方向饶原点旋转一定的角度θ,自由度为1,不包含平移,如顺时针旋转可以表示为:
翻转
翻转是x或y某个方向或全部方向上取反,自由度为2,比如这里以垂直翻转为例:
刚体变换
旋转+平移也称刚体变换(Rigid Transform),就是说如果图像变换前后两点间的距离仍然保持不变,那么这种变化就称为刚体变换。刚体变换包括了平移、旋转和翻转,自由度为3。由于只是旋转和平移,刚体变换保持了直线间的长度不变,所以也称欧式变换(变化前后保持欧氏距离)。变换矩阵可以表示为:
缩放
缩放是x和y方向的尺度(倍数)变换,在有些资料上非等比例的缩放也称为拉伸/挤压,等比例缩放自由度为1,非等比例缩放自由度为2,矩阵可以表示为:
相似变换
相似变换又称缩放旋转,相似变换包含了旋转、等比例缩放和平移等变换,自由度为4。在OpenCV中,旋转就是用相似变换实现的:
若缩放比例为scale,旋转角度为θ,旋转中心是(centerx,centery),则仿射变换可以表示为:
其中:
相似变换相比刚体变换加了缩放,所以并不会保持欧氏距离不变,但直线间的夹角依然不变。
透视变换
前面仿射变换后依然是平行四边形,并不能做到任意的变换。
原理
透视变换(Perspective Transformation)是将二维的图片投影到一个三维视平面上,然后再转换到二维坐标下,所以也称为投影映射(Projective Mapping)。简单来说就是二维→三维→二维的一个过程。
透视变换公式:
透视变换矩阵表示:
仿射变换是透视变换的子集。接下来再通过除以Z轴转换成二维坐标:
透视变换相比仿射变换更加灵活,变换后会产生一个新的四边形,但不一定是平行四边形,所以需要非共线的四个点才能唯一确定,原图中的直线变换后依然是直线。因为四边形包括了所有的平行四边形,所以透视变换包括了所有的仿射变换。
opencv中实现透视变换
OpenCV中首先根据变换前后的四个点用cv.getPerspectiveTransform()生成3×3的变换矩阵,然后再用cv.warpPerspective()进行透视变换。
import numpy as np
import cv2 as cv
import matplotlib.pyplot as plt
img = cv.imread('card.jpg')
# 原图中卡片的四个角点
pts1 = np.float32([[148, 80], [437, 114], [94, 247], [423, 288]])
# 变换后分别在左上、右上、左下、右下四个点
pts2 = np.float32([[0, 0], [320, 0], [0, 178], [320, 178]])
# 生成透视变换矩阵
M = cv.getPerspectiveTransform(pts1, pts2)
# 进行透视变换,参数3是目标图像大小
dst = cv.warpPerspective(img, M, (320, 178))
plt.subplot(121), plt.imshow(img[:, :, ::-1]), plt.title('input')
plt.subplot(122), plt.imshow(dst[:, :, ::-1]), plt.title('output')
plt.show()
实验结果

总结
图解图像各种变换
质总结](https://img-blog.csdnimg.cn/2020032911012244.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0liZWxpZXZlc3Vuc2hpbmU=,size_16,color_FFFFFF,t_70#pic_center)