目录

1.VAE 概述

2.概率分布

3.损失函数

4.重参数技巧

5.维度对 VAE 的影响

6.损失函数对VAE的影响

7.总结

---

VAE原始https://arxiv.org/abs/1312.6114

论文解读：https://mp.weixin.qq.com/MzI1MjQ2O

1.VAE 概述

        变分自动编码器（Variational autoEncoder，VAE）是生成模型的一种。这些方法的主要目标是从对象的学习分布中生成新的采样数据。2014 年，Kingma et al.提出了这种 VAE生成模型，该模型可以从隐变量空间的概率分布中学习潜在属性并构造新的元素。

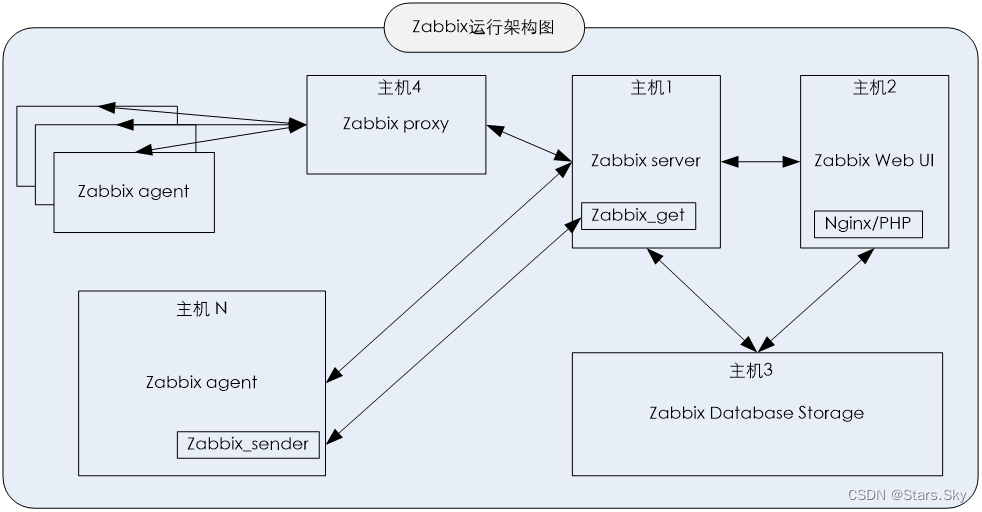
        VAE 包含两个部分：编码器 encoder 和解码器 decoder。如图所示，编码器计算每个输入数据X ={X1,X2...,Xn}的低维均值和方差，然后从隐变量空间采样，得到Z={Z1,Z ...,Zn}，通过解码器生成新数据Y ={Y1,Y2...,Yn}。我们希望从隐变量空间中的采样的数据 Z 遵循原始数据 X 的概率分布，这样根据采样数据 Z 生成的新数据 Y也就可以遵循原始数据的概率分布。

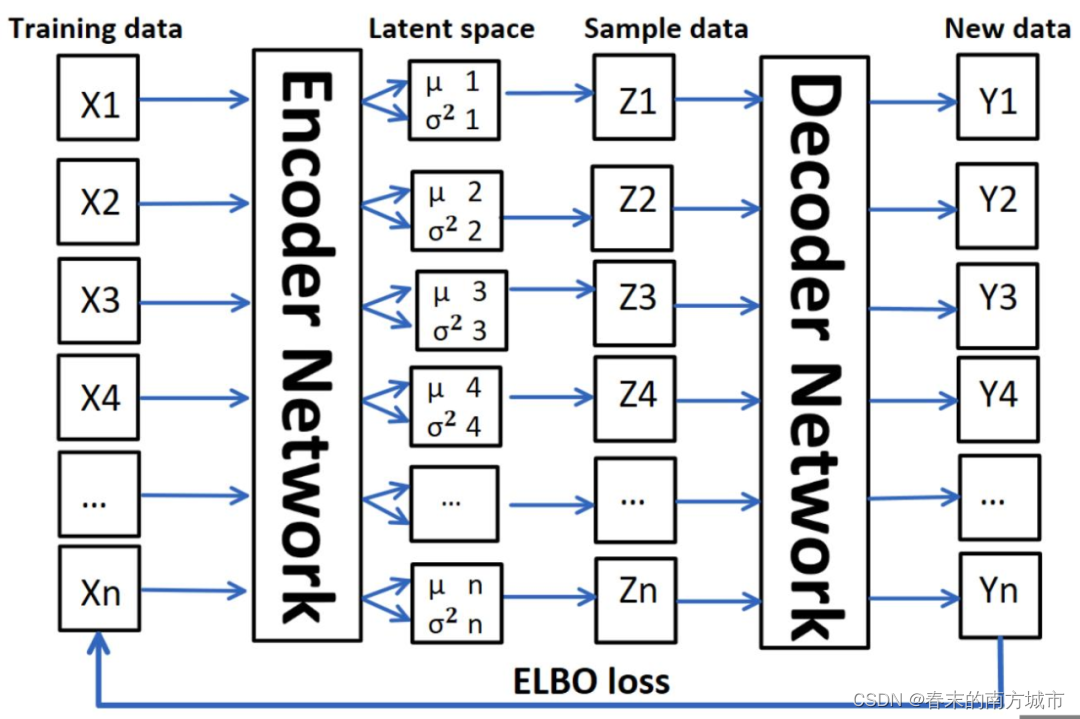
                                                                        图1 VAE结构图

2.概率分布

        为了确保采样数据 Z 的概率分布符合输入 X ，首先假设存在一个 Z 关于 X 的后验后验概率，并进一步假设这个概率分布是正态分布：

p(Z | X ) = N(0, I)

那么采样数据 Z 的概率分布就为：

这样p(Z) (先验分布)和p(Z|X) (后验分布)就都符合标准正态分布了。

3.损失函数

        VAE 生成图片的性能可以通过 evidence lower bound（ELBO) loss 来评估，该损失由Reconstruction loss 和 Kullback–Leibler loss(KL loss)组成。Reconstruction loss 用于计算生成的数据与原始数据的相似程度，而 KL loss 作为一个额外的 loss，用于测量一般正态分布与标准正态分布的差异，也就是均值和方差之间的差异。在给定的隐变量空间维度为 n 的条件下，已知均值和方差，则KL loss 定义为:

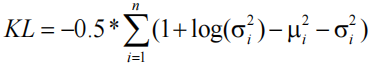
        Reconstruction loss 使用标准的L2 Loss也就是 MSE。给定 m 个数据，已知真实值 x 和预测值x^。Reconstruction loss 定义为：

        最终，ELBO loss 由上述两个损失函数组成，系数为 α 和 β：

        简单来说，这里的 Reconstruction loss 是用来让 decoder 的输出 Y 和输入 X 尽可能相似。而 KL loss 希望隐变量空间可以符合标准的正态分布，但实际 X 的分布其实并不是标准的正态分布，也就是说 KL loss 会让输出 Y 具有多样性，与输入 X 产生一部分的差异。Reconstruction loss 和 KL loss 的比例是 1：1，这样既能保证生成图像质量，又可以引入一定的噪声，使生成图片有一定的泛化能力。

4.重参数技巧

        除了这个特殊的损失函数，作者还介绍了一种名为重参数技巧（Reparameterizationtrick）的方法。

                                                               图2重参数技巧

        因为假设 p(Z | X ) = N(0, I) , 但是均值和方差都是靠 encoder 计算出来的，然后我们要靠这个均值和方差反向优化 encoder。但是随机采样这个操作是不可导的，我们不可能通过随机采样操作进行反向传播。因此我们可以利用随机采样的结果，本来我们需要从均值和方差的分布中随机采样，现在我们只需要生成一组符合正态分布的变量ε。如图2所示，从正态分布中采样一个 Z，相当于从 N(0,I) 中采样一个 ε，然后让

这样随机采样就不用参与梯度下降了，只需要更新采样的结果。

5.维度对 VAE 的影响

        在变分自编码器中，隐变量空间的维度（dimensionality）是一个非常重要的变量，在一般的编码器（AE）中，这个变量也被称为 bottleneck。如果给定 m 个数据，维度的大小为 n，那么每个数据就会产生 n 个均值和 n 个方差。不同的维度会导致 decoder 生成不同的图片，我们这里使用 MNIST 的训练集，在ELBO = 0.5*MSE + 0.5*KL的情况下来训练变分自动编码器，用 MNIST 的测试集来测试重构的效果。如图 5，在维度为 2，5，10，20 的情况下，左边图片代表 ground truth，也就是 encoder 的输入，右边图片代表生成的图片，也就是 decoder 的输出。

                                                        图5 GT与不同维数重建的比较

        我们可以看出，在隐变量空间的维度较低时，生成的数字较为模糊，在隐变量空间的维度较高时，生成的数字相对而言噪声小，更加清晰，并且与原图像有着一定的相似度。

6.损失函数对VAE的影响

        从第五节可以看出，不同维度的大小会影响生成图片的质量。同样的，不同的损失函数也会导致 VAE 生成不同质量的图片。在第三节的最后一段我们提到过，Reconstruction loss 希望输出和输出保持相同，而 KL loss 在原有的基础上引入了一定的噪声。因此，我们可以通过修改两个损失函数的权重，来控制不同的损失函数对输出的影响程度。在 0.1*MSE + 0.9*KL 0.9*MSE + 0.1*KL 的情况下，生成的图片又会有什么差别呢？图 6 展示了不同损失函数下生成图片的质量（隐变量空间维度为 20），就像我们想得那样，在 MSE 权重较大的情况下，生成的图片几乎与原图片一模一样，几乎没有噪声。而在 KL loss 占主导时，生成的图片由于噪声过大已经完全看不出来是什么了。

                                                   图6 GT与基于不同损失函数的重建的比较

        除了观察生成的图片的质量，我们还可以通过对隐变量空间的分析来查看数据的分布情况。当 MSE 权重较大的时候（0.9*MSE + 0.1*KL），隐变量空间的分布情况更像原数据的分布情况。

7.总结

        尽管 VAE 在名字上很像 AE（自动编码器），但其方法（或其对网络的解释）是独特的。在 VAE 中 ，encoder 用于计算平均值和方差，这与平时的 AE 完全不是一个类型的模型。对于不同的隐变量空间维度，VAE 具有不同的性能，相对而言，隐变量空间越大，可以保留的概率分布的信息就越多。但我们并不能说，隐变量空间越大就一定越好，考虑一个极限的情况就是当输入图片是 28*28*1 的情况下，隐变量空间的大小设置为 784，也就是原数据的大小，VAE 也就失去了 encoding 的意义了。

        对于损失函数 ELBO loss，我们可以调整它的权重来达到不同的生成效果，毕竟我们在生活中也会遇到相当多的噪声，这对于模型的鲁棒性来说是非常有意义的。除了VAE，后续还有很多类似的模型比如条件变分自编码器（Conditional VariationalautoEncoder），生成对抗编码器（VAEGAN）等等。