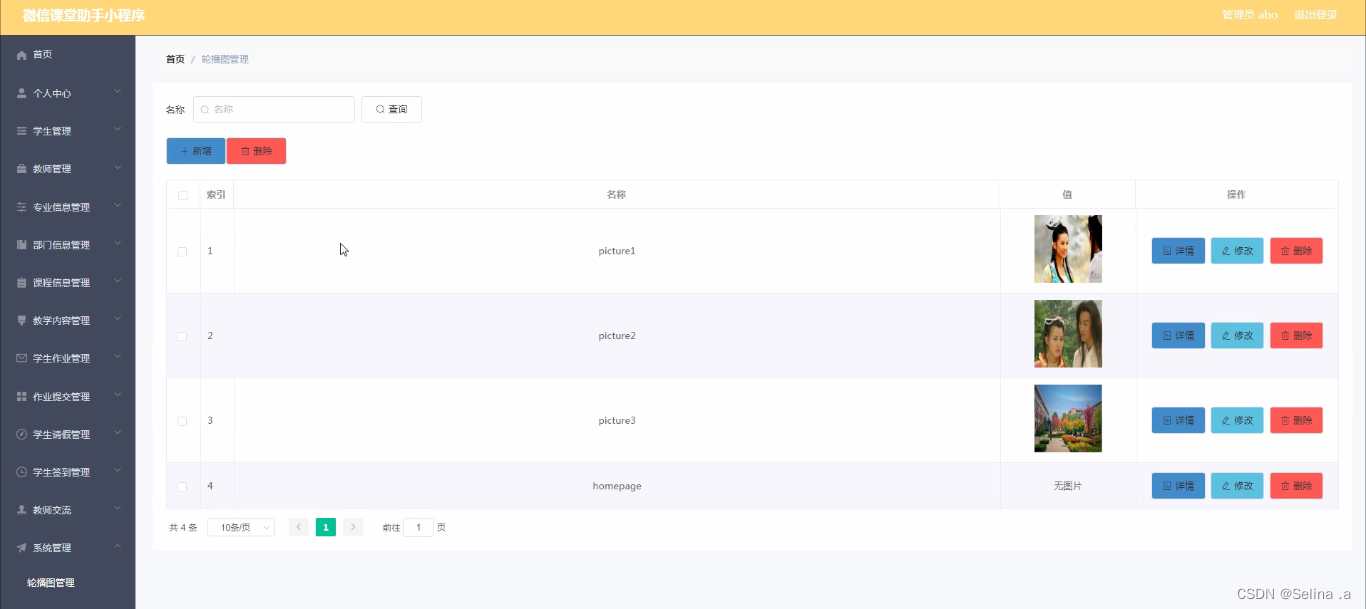
题目描述：

[实验题目1]

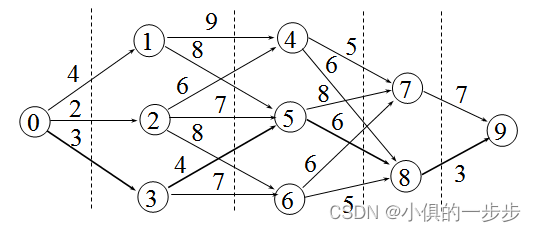
设图G=(V, E)是一个带权有向图，如果把顶点集合V划分成k个互不相交的子集Vi (2≤k≤n, 1≤i≤k)，使得E中的任何一条边(u, v)，必有u∈Vi，v∈Vi+m (1≤i≤k, 1＜i+m≤k)，则称图G为多段图，称s∈V1为源点，t∈Vk为终点。多段图的最短路径问题求从源点到终点的最小代价路径。

 

实验目的

(1)掌握动态规划法的设计思想；

(2)掌握填表过程以及求解方法。

实验要求

(1)确定多段图的存储结构。

(2)设计动态规划法的填表过程和求解方法；

(3)设计测试数据，并讨论所得结果。

核心思想：

将图使用邻接矩阵保存

一个数组value保存从源头点到当前点的最短路径；

一个数组parent保存到达当前点的上一个点；

是否选择是否走该顶点依据：min(value[j]+arr[j][i]，value[i]) 

最后使用parent追溯所走的路径，将点存储到栈中。

表记录： 

顶点	value	parent
0	0	-1
1	4	0
2	2	0
3	3	0
4	10	2
5	7	3
6	10	3
7	15	5
8	13	5
9	16	8

 

import java.util.Arrays;
import java.util.Stack;

public class Main1 {
    public static void main(String[] args) {
        int[][] arr = { {0,4,2,3,0,0,0,0,0,0},
                        {0,0,0,0,9,8,0,0,0,0},
                        {0,0,0,0,8,7,8,0,0,0},
                        {0,0,0,0,0,4,7,0,0,0},
                        {0,0,0,0,0,0,0,5,6,0},
                        {0,0,0,0,0,0,0,8,6,0},
                        {0,0,0,0,0,0,0,6,5,0},
                        {0,0,0,0,0,0,0,0,0,7},
                        {0,0,0,0,0,0,0,0,0,3},
                        {0,0,0,0,0,0,0,0,0,0}
                                                };
         int res =  getSortPath(arr);
        System.out.println("最短路径值为："+res);
    }
    public static int getSortPath(int[][] arr){
        int n = arr.length;
        //存储最短路径
        int[] value = new int[n];
        Arrays.fill(value,Integer.MAX_VALUE);
        //存储i节点的前驱节点
        int[] parent = new int[n];
        Arrays.fill(parent,-1);
        value[0] = 0;
        for (int i = 1; i <n ; i++) {
            for (int j = i-1; j >=0 ; j--) {
                if (arr[j][i]!=0&&value[j]+arr[j][i]<value[i]){
                    value[i] = value[j]+arr[j][i];
                    parent[i] = j;
                }
            }
        }
        //用来保存路径
        Stack<Integer> path = new Stack<Integer>();
        int i = n-1;
        path.push(i);
        while (i>0){
            path.push(parent[i]);
            i = parent[i];
        }
        System.out.print("最短路径为：");
        while (!path.isEmpty()){
            System.out.print(path.pop()+"--->");
        }
        System.out.println();
        return value[n-1];
    }
}

输出结果：