力扣日记:【二叉树篇】二叉树的最大深度
日期:2023.11.27
参考:代码随想录、力扣
104. 二叉树的最大深度
题目描述
难度:
给定一个二叉树 root ,返回其最大深度。
二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。
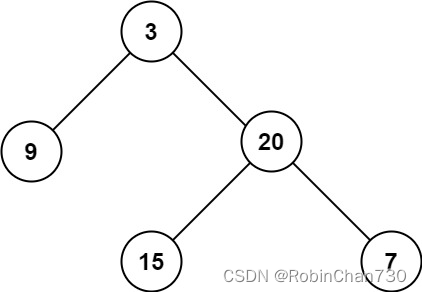
示例 1:
输入:root = [3,9,20,null,null,15,7]
输出:3
示例 2:
输入:root = [1,null,2]
输出:2
提示:
- 树中节点的数量在 [0, 10^4] 区间内。
- -100 <= Node.val <= 100
题解
递归法(cpp ver)
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
// 递归法:后序遍历 (实际上是求高度)
// 1. 确定递归函数的参数和返回值:参数就是传入树的根节点,返回就返回以该节点为根的树的深度
int getdepth(TreeNode* node) {
// 2. 确定终止条件:如果为空节点的话,就返回0,表示高度为0。
if (node == NULL) return 0;
// 3. 确定单层递归的逻辑:先求它的左子树的深度,再求右子树的深度,最后取左右深度最大的数值 再+1 (加1是因为算上当前中间节点)就是目前节点为根节点的树的深度。
int leftdepth = getdepth(node->left); // 左(左子树的高度)
int rightdepth = getdepth(node->right); // 右(右子树的高度)
int depth = 1 + max(leftdepth, rightdepth); // 中(左子树和右子树的根节点的高度, 包括根节点, 故+1)
return depth;
}
int maxDepth(TreeNode* root) {
return getdepth(root);
}
};
迭代法(go ver)
/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func maxDepth(root *TreeNode) int {
// 使用迭代法的话,使用层序遍历是最为合适的,因为最大的深度就是二叉树的层数,和层序遍历的方式极其吻合
queue := list.New()
maxDepth := 0
if root != nil {
queue.PushBack(root)
}
for queue.Len() > 0 {
// 记录当前队列长度
size := queue.Len()
for size > 0 {
// 弹出并写入结果
front := queue.Front()
node := queue.Remove(front).(*TreeNode) // 存进list之后类型会变为*list.Element,要转换为*TreeNode
// 左右节点入队列
if node.Left != nil {
queue.PushBack(node.Left)
}
if node.Right != nil {
queue.PushBack(node.Right)
}
size -= 1
}
maxDepth += 1
}
return maxDepth
}
复杂度
时间复杂度:
空间复杂度:
思路总结
- 本题如果用迭代法,则直接使用层序遍历的模板解题即可
- 如果用递归法,则相对难一些:
- 首先要理解二叉树的深度和高度区别:
- 二叉树节点的深度:指从根节点到该节点的最长简单路径边的条数或者节点数(取决于深度从0开始还是从1开始)—— 即深度是从某节点角度往上(根节点)看的
- 二叉树节点的高度:指从该节点到叶子节点的最长简单路径边的条数或者节点数(取决于高度从0开始还是从1开始)—— 即高度是从某节点角度往下(叶子节点)看的
- 因此,根节点的高度就是二叉树的最大深度
- 本题可以使用前序(中左右),也可以使用后序遍历(左右中),使用前序求的就是深度,即最大的叶子节点深度,使用后序求的是高度,即根节点的高度。(后序遍历相对容易理解一些,见代码)
- 首先要理解二叉树的深度和高度区别: