Java PriorityQueue

news2024/11/27 14:34:15

一般情况下, 我们使用队列是为了能够建造队列的先进先出 (First-In-First-Out) 模式的, 达到一种资源的公平分配, 先到达的任务 (元素) 先处理, 但有时需要在队列中基于优先级处理对象。
存入队列中的任务 (元素) 具有优先级, 需要根据优先级修复里面的数据。而在 JDK 1.5 引入的 PriorityQueue, 就具备了这种功能。

1 PriorityQueue 的实现数据结构

PriorityQueue 通过二叉小顶堆实现, 具备下面的特点:

  1. 二叉堆就是完全二叉树, 左边最多比右边深 1 层, 不能是右边比左边深, 这是和平衡二叉树不同的地方。在树中的数据变动了 (新增/删除等), 具备自行调整的特性。
  2. 小顶堆: 根节点最小, 父结点的键值总是小于或等于任何一个子节点的键值 (大顶堆, 则是相反的)。

基于上面的 2 个特性, 可以推导出几个特点 (假设当前有一个节点 Node, 从上往下, 从左往右计算, 他是 index 个)

  1. Node 节点的左子节点的位置为 2 * index + 1
  2. Node 节点的右子节点的位置为 2 * index + 2
  3. Node 节点的父级节点的位置为 (index - 1) / 2

每个节点可以推导出其相关的父子级节点, 所以二叉小顶堆可以通过数组优雅的实现。

如图:
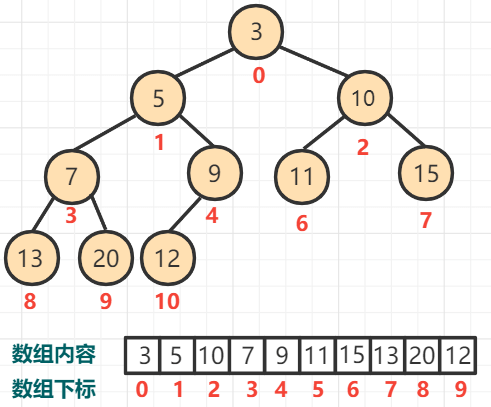
Alt '数组实现 PriorityQueue'

2 PriorityQueue 中的几比较重要的属性

public class PriorityQueue<E> {

    transient Object[] queue; 

    private int size = 0;

    private final Comparator<? super E> comparator;

    transient int modCount = 0;
}

2.1 queue

PriorityQueue 中数据存储的地方, 可以看到是通过数组实现, 通过数组实现了二叉小顶堆的结构。

2.2 size

当前 PriorityQueue 中存储的数据量

2.3 comparator

用户自定义的比较器, PriorityQueue 就是借助这个比较器, 对存入的数据进行比较, 决定优先级的。
如果用户没有定义这个比较器的话, 那么需要保证存入 PriorityQueue 中的数据是可以比较的, 即实现了 Comparator 接口。
而当用户既定义了比较器, 同时数据实现了 Comparator 接口, 优先使用比较器进行比较。

2.4 modCount

当前的 PriorityQueue 变更了多少次。

3 PriorityQueue 的构造方法

public class PriorityQueue<E> {

    // 构造函数 1: 无参构造函数
    public PriorityQueue() {
        // 省略    
    }

    // 构造函数 2: 指定容量的构造函数
    public PriorityQueue(int initialCapacity) {
        // 省略
    }

    // 构造函数 3: 指定容量比较器的构造函数
    public PriorityQueue(Comparator<? super E> comparator) {
        // 省略
    }

    // 构造函数 4: 指定了初始容量和比较器的构造函数
    public PriorityQueue(int initialCapacity,  Comparator<? super E> comparator) {
        // 省略
    }

    // 构造函数 5: 指定一个 PriorityQueue 的构造函数
    public PriorityQueue(PriorityQueue<? extends E> c) {
        // 省略
        this.comparator = (Comparator<? super E>) c.comparator();
        initFromPriorityQueue(c);
    }

    // 构造函数 6: 指定一个  SortedSet 的构造函数
    public PriorityQueue(SortedSet<? extends E> c) {
        this.comparator = (Comparator<? super E>) c.comparator();
        initElementsFromCollection(c);
    }

    // 构造函数 7: 给定一个 Collection 的构造函数
    public PriorityQueue(Collection<? extends E> c) {
        // 省略
    }
}

总共提供了 7 个构造函数, 看起来很多, 实际后面很多都是相同的, 所以需要深入理解的就 1 个, 指定 Collection 的构造函数。

3.1 无参构造函数

public PriorityQueue() {
    // 内部调用到自身 2 个参数的构造函数
    // 同时提供默认值, 初始容量的默认值为 DEFAULT_INITIAL_CAPACITY = 11, Comparator 比较器为null
    this(DEFAULT_INITIAL_CAPACITY, null);
}

3.2 指定容量的构造函数

public PriorityQueue(int initialCapacity) {
    // 同样是内部调用到自身的 2 个参数的构造函数
    // 初始容量默认值为用户定义的值, Comparator 比较器则为 null
    this(initialCapacity, null);
}

3.3 指定容量比较器的构造函数

public PriorityQueue(Comparator<? super E> comparator) {
    // 同样是内部调用到了自身的 2 个参数的构造函数
    // 初始容量默认为 11, 比较器为用户自定义的
    this(DEFAULT_INITIAL_CAPACITY, comparator);
}

3.4 指定了初始容量和比较器的构造函数

public PriorityQueue(int initialCapacity,  Comparator<? super E> comparator) {
    // 初始容量必须大于 1 
    if (initialCapacity < 1)
        throw new IllegalArgumentException();

    // 声明数组
    this.queue = new Object[initialCapacity];
    // 将用户声明的比较器赋值给自身的比较器属性
    this.comparator = comparator;
}

3.5 指定一个 PriorityQueue 的构造函数

public PriorityQueue(PriorityQueue<? extends E> c) {
    // 获取队列里面的比较器
    this.comparator = (Comparator<? super E>) c.comparator();
    // 将队列里面的数据读取到自身, 下面集合构造函数分析
    initFromPriorityQueue(c);
}

3.6 指定一个 SortedSet 的构造函数

public PriorityQueue(SortedSet<? extends E> c) {
    // 获取 SortedSet 里面的比较器
    this.comparator = (Comparator<? super E>) c.comparator();
    // 从集合里面读取数据到自身, 同样下面的集合构造函数有分析
    initElementsFromCollection(c);
}

3.7 给定一个 Collection 的构造函数

public PriorityQueue(Collection<? extends E> c) {
    
    if (c instanceof SortedSet<?>) {
        // SortedSet 内部也是有序的, 实现逻辑也是和 PriorityQueue 一样, 所以特殊处理
        SortedSet<? extends E> ss = (SortedSet<? extends E>) c;
        // 获取 SortedSet 中的比较器
        this.comparator = (Comparator<? super E>) ss.comparator();

        // 从 Collection 中获取数据赋值到当前的 PriorityQueue
        initElementsFromCollection(ss);

    } else if (c instanceof PriorityQueue<?>) {
        // PriorityQueue 转为 PriorityQueue, 逻辑简单很多, 所以特殊处理
        PriorityQueue<? extends E> pq = (PriorityQueue<? extends E>) c;
        // 获取 PriorityQueue 的比较器
        this.comparator = (Comparator<? super E>) pq.comparator();
        // 获取数据
        initFromPriorityQueue(pq);

    } else {
        // 设置当前的 PriorityQueue 的比较器为 null
        this.comparator = null;
        // 获取数据
        initFromCollection(c);
    }
}

/**
 * 场景一: 从有序的结合中获取数据 
 */
private void initElementsFromCollection(Collection<? extends E> c) {
    
    // 调用这个方法的调用方, Colleciont 是已经有序的

    // 转换数组
    Object[] a = c.toArray();

    // 不是 ArrayList 类型, 通过 Arrays.copyOf 做一层转换
    if (c.getClass() != ArrayList.class)
        a = Arrays.copyOf(a, a.length, Object[].class);

    int len = a.length;
    // 只有 1 个元素 或者 自定义的比较器不为 null
    if (len == 1 || this.comparator != null)
        // 不能为 null
        for (int i = 0; i < len; i++)
            if (a[i] == null)
                throw new NullPointerException();
    // 赋值给自身的 queue 数组      
    this.queue = a;
    // 当前的个数等于数组的长度
    this.size = a.length;
}

/**
 * 场景二: 从 PriorityQueue 中获取数据
 */
private void initFromPriorityQueue(PriorityQueue<? extends E> c) {
    // 是 PriorityQueue 直接赋值
    if (c.getClass() == PriorityQueue.class) {
        this.queue = c.toArray();
        this.size = c.size();
    } else {
        initFromCollection(c);
    }
}

/**
 * 场景三: 从普通的集合中获取数据
 */
private void initFromCollection(Collection<? extends E> c) {

    // 调用这个方法的调用方, Collection 不一定是有序的, 所以为了满足二叉小顶堆的特点, 需要进行堆化调整

    // 把 Collection c 中的数据赋值给当前的 Queue
    initElementsFromCollection(c);
    // 堆化, 数组调整, 使其满足二叉小顶堆的特点
    heapify();
}

private void heapify() {

    // 对于一个杂乱无章的数组, 进行调整的话, 如果直接从第一个元素开始调整, 那么会频繁的调整
    // 通过分析可以知道, 二叉树没有叶子节点占整棵树节点的一半, 所有的叶子节点暂时不看他们的父级节点, 可以看做是已经满足二叉树的节点
    // 这一部分看做是满足条件的话, 那么就可以从最后一个有叶子节点的开始往前进行调整, 这样的话, 可以只对数组中的一半进行调整

    // 从数组的中间开始调整
    for (int i = (size >>> 1) - 1; i >= 0; i--)
        // 下移操作, 后面讲解
        siftDown(i, (E) queue[i]);
}

4 PriorityQueue 的操作方法

4.1 添加数据

二叉小顶堆的特点

  1. 父结点的键值总是小于或等于任何一个子节点的键值
  2. 于数组实现的二叉堆, 对于数组中任意位置的 n 上元素, 其左孩子在 2n+1 位置上, 右孩子 2(n+1) 位置, 它的父亲则在 n-1/2 上, 根节点在 0 位置

为了维护这个特点, 二叉堆在添加元素的时候, 需要一个 “上移” 的动作, “上移” 的过程, 如图:

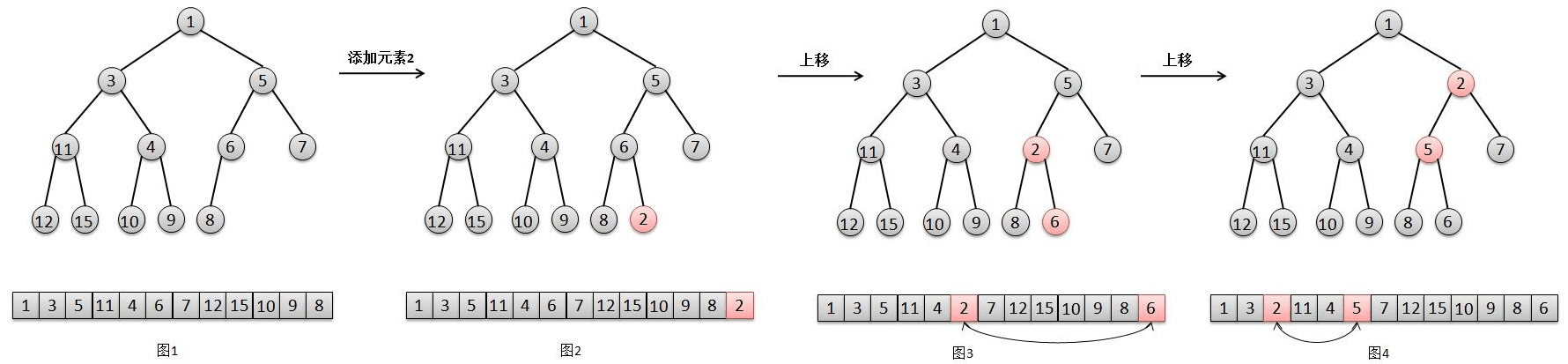
Alt 'BinaryHeapShiftUp'

  1. 将元素 2 添加在最后一个位置
  2. 由于 2 比其父亲 6 要小, 所以将元素 2 上移, 交换 2 和 6 的位置
  3. 然后由于 2 比 5 小, 继续将 2 上移, 交换 2 和 5 的位置
  4. 此时 2 大于其父亲 (根节点) 1, 结束

上移的过程总结

  1. 先把需要新增的节点放到末尾的位置
  2. 和其父级进行比较

2.1 如果没有父节点了, 结束, 当前的位置就是新增节点的位置
2.1 如果比父级的值大, 结束, 这个位置就是新增的节点的所在位置
2.2 如果比父级的值小, 和父级交互值, 然后回到第二步, 继续进行比较

代码实现:

public class PriorityQueue<E> {

    public boolean add(E e) {
        // 默认添加到尾部, 调用自身的 offer 方法
        return offer(e);
    }

    public boolean offer(E e) {
        // 不支持 null
        if (e == null)
            throw new NullPointerException();
        // 修改次数 +1            
        modCount++;
        // 当前数据的个数
        int i = size;
        // 数据的个数大于当前数组的长度
        if (i >= queue.length)
            // 扩容
            grow(i + 1);
        // 已存储数据个数 + 1            
        size = i + 1;
        // 当前数组中的没有数据
        if (i == 0)
            // 直接把数组的第一位设置为添加的数据
            queue[0] = e;
        else
            // 添加数据到数组的 i 位置并进行上移操作
            siftUp(i, e);
        return true;
    }
    
    // 元素上移
    private void siftUp(int k, E x) {
        if (comparator != null)
            // 有比较器的使用比较器的上移方法
            siftUpUsingComparator(k, x);
        else
            // 没有比较器使用, 没有比较器的的上移方法
            siftUpComparable(k, x);
    }

    // 使用用户自定义的比较器进行比较, 然后完成元素上移操作
    private void siftUpUsingComparator(int k, E x) {

        while (k > 0) {
            // 获取插入位置的父级节点的位置
            int parent = (k - 1) >>> 1;
            // 获取父级节点的值
            Object e = queue[parent];
            // 使用比较器进行比较当前的值和父级的值, 
            // 当前的值 >= 父级的值, 不需要上移了, 此时的 k 位置就是数据存储的位置
            if (comparator.compare(x, (E) e) >= 0)
                break;
            // 当前的位置设置为父级的值                
            queue[k] = e;
            // 将父级的位置赋给当前的 k, 标识下次计划插入的位置, 也就是上移操作
            k = parent;
        }
        // 数组当前的 k 位置等于需要插入的数据 x
        queue[k] = x;

    }

    // 使用元素的比较器进行比较, 然后完成元素上移操作
    private void siftUpComparable(int k, E x) {
        // 没有比较器, 需要当前的数据是 Comparable 的实现类, 即数据类型是可比较的
        Comparable<? super E> key = (Comparable<? super E>) x;
        // 大体的流程和上面的一样
        while (k > 0) {
            int parent = (k - 1) >>> 1;
            Object e = queue[parent];
            if (key.compareTo((E) e) >= 0)
                break;
            queue[k] = e;
            k = parent;
        }
        queue[k] = key;
    }

    // 数组扩容
    private void grow(int minCapacity) {

        // 当前数组的容量
        int oldCapacity = queue.length;
        // 当前数组的容量 < 64, 则新的数组容量 = 旧数组容量 * 2 + 2, 否则等于新的数组容量 = 旧的容量 * 1.5
        int newCapacity = oldCapacity + ((oldCapacity < 64) ? (oldCapacity + 2) : (oldCapacity >> 1));

        // 新的容量比最大值 (int 的最大值 - 8) 大
        if (newCapacity - MAX_ARRAY_SIZE > 0)
            // 控制新的最大值不大于 int 的最大值
            newCapacity = hugeCapacity(minCapacity);

        // 声明新的数组, 同时将旧的数组的数据迁移到新的数组
        queue = Arrays.copyOf(queue, newCapacity);            
    }

    private static int hugeCapacity(int minCapacity) {
        // 小于 0, 抛异常
        if (minCapacity < 0) 
            throw new OutOfMemoryError();
        // 入参的容量大于 int 的最大值 - 8 的话, 返回 int 的最大值, 否则返回 int 的最大值 - 8
        return (minCapacity > MAX_ARRAY_SIZE) ? Integer.MAX_VALUE : MAX_ARRAY_SIZE;
    }
}

4.2 删除数据

对于 PriorityQueue 删除数据都是删除根元素, 也就是最小的元素。
删除了根元素, 就要找一个替代者移动到根位置, 相对于被删除的元素来说就是 “下移”, 如图:
Alt 'BinaryHeapShiftDown'

  1. 将找出队尾的元素 8, 并将它在队尾位置上删除
  2. 此时队尾元素 8 比根元素 1 的最小孩子 3 要大, 所以将元素 1 下移, 交换 1 和 3 的位置
  3. 然后此时队尾元素 8 比元素 1 的最小孩子 4 要大, 继续将 1 下移, 交换 1 和 4 的位置
  4. 然后此时根元素 8 比元素 1 的最小孩子 9 要小, 不需要下移, 直接将根元素 8 赋值给此时元素 1 的位置, 1 被覆盖则相当于删除

下移的过程总结

  1. 获取末尾节点的值, 然后进行删除
  2. 找到需要删除位置的左右节点, 找到 2 个节点值比较小的节点

2.1 如果没有左右节点, 把末尾节点的值放到这个位置, 下移过程结束
2.2 如果只有左节点, 较小值等于左节点的值

  1. 用末尾的值和找到的较小值比较

3.1 如果末尾的值比较小值小, 那么需要删除位置放入末尾节点的值, 下移结束
3.2 如果末尾的值比较小值大, 那么把较小值的放到需要删除的位置, 需要删除的位置替换为较小值所在的位置, 然后回到第二步, 继续进行比较

如果删除的位置刚好是根节点, 上面的下移基本完成了。

如果删除的位置是中间的位置, 那么还需要在进行一次是否上移的判断:
如果末尾的值直接就是放入第一次需要删除的位置, 没有任何的比较替换操作, 这是放入的位置的值可能比他的父级小, 所以还需要进行一次上移的判断,
如果不是直接放入到第一次需要删除的位置, 就不需要进行上移的判断

代码实现:

public class PriorityQueue<E> {

    public E remove() {
        E x = poll();
        if (x != null)
            return x;
        else
            // 为 null 抛出异常
            throw new NoSuchElementException();
    }

    public E poll() {
        // 存储的数据个数为 0, 返回 null
        if (size == 0)
            return null;
        // 新的元素个数 = 旧的元素个数 - 1    
        int s = --size;
        // 修改次数 + 1
        modCount++;
        // 获取根节点
        E result = (E) queue[0];
        // 获取最后一个节点
        E x = (E) queue[s];
        // 设置最后一个节点为 null
        queue[s] = null;
        // 新的元素个数不等于 0, 进行下移
        if (s != 0)
            siftDown(0, x);  
        return result;
    }

    private void siftDown(int k, E x) {
        // 将元素 x 放入到 k 的位置, 然后进行下移
        if (comparator != null)
            siftDownUsingComparator(k, x);
        else
            siftDownComparable(k, x);
    }
    
    // 使用用户自定义的比较器进行比较, 然后完成元素下移操作
    private void siftDownUsingComparator(int k, E x) {
        
        // 通过 size/2 找到第一个没有叶子节点的元素, 这个位置后面的节点都是没有叶子节点, 可以不用处理了
        int half = size >>> 1;
        

        while (k < half) {

            // 获取指定位置的左节点
            int child = (k << 1) + 1;

            // c 存储的是左右节点中较小的值
            Object c = queue[child];

            // 右节点的位置
            int right = child + 1;

            // 不是数组的尾部, 左节点比右节点的值大, 那么较小值 c = 右节点的值
            if (right < size && comparator.compare((E) c, (E) queue[right]) > 0)
                // 需要替换的值为右节点的值
                c = queue[child = right];

            // 需要替换的值比左右节点中的较小值还要小, 不需要继续处理了
            if (comparator.compare(x, (E) c) <= 0)
                break;

            // 将 x 理论存储的位置从 k 下移到左右节点中较小的节点的位置 child, 进入下层循环
            queue[k] = c;
            k = child;
        }

        // 将 x 值放到 k 位置
        queue[k] = x;
    }

    // 使用元素的的比较器进行比较, 然后完成元素上移操作
    private void siftDownComparable(int k, E x) {
        // 和上面的逻辑差不多
        Comparable<? super E> key = (Comparable<? super E>)x;
        int half = size >>> 1;   
        while (k < half) {
            int child = (k << 1) + 1; 
            Object c = queue[child];
            int right = child + 1;
            if (right < size &&  ((Comparable<? super E>) c).compareTo((E) queue[right]) > 0)
                c = queue[child = right];
            if (key.compareTo((E) c) <= 0)
                break;
            queue[k] = c;
            k = child;
        }
        queue[k] = key;
    }
}

队列基本的操作只有入队和出队, 几乎没有查询的操作, 所以 PriorityQueue 的代码分析就到这里。

5 使用场景

ProfityQueue 在一些调度和算法中使用比较多

  1. 带有优先级任务的调度, 比如什么加急审批
  2. 负载均衡, 可以根据流量等因素进行优先级的调度
  3. 一些搜索算法

6 参考

PriorityQueue源码分析

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1257207.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

python爬虫进阶篇（异步）

python爬虫进阶篇（异步）

学习完前面的基础知识后&#xff0c;我们会发现这些爬虫的效率实在是太低了。那么我们需要学习一些新的爬虫方式来进行信息的获取。 异步 使用python3.7后的版本中的异步进行爬取&#xff0c;多线程虽然快&#xff0c;但是异步才是爬虫真爱。 基本概念讲解 1.什么是异步&…
阅读更多...
光线追踪-Peter Shirley的RayTracing In One Weekend系列教程（book1-book3）代码分章节整理

光线追踪-Peter Shirley的RayTracing In One Weekend系列教程（book1-book3）代码分章节整理

自己码完了一遍了&#xff0c;把代码分章节整理了一下&#xff0c;可以按章节独立编译&#xff0c;运行, 也可以直接下载编译好的release版本直接运行。 项目地址&#xff1a; Github: https://github.com/disini/RayTracingInOneWeekendChaptByChapt ​ ​ ​ ​
阅读更多...
【赠书第8期】工程效能十日谈

【赠书第8期】工程效能十日谈

文章目录 前言 1 工程效能十日谈 1.1 制定清晰的目标和计划 1.2 引入先进的技术和工具 1.3 建立有效的沟通机制 1.4 灵活应对变化 1.5 确保资源充足 1.6 进行有效的风险管理 1.7 进行持续的监控和评估 1.8 优化团队合作 1.9 注重质量管理 1.10 进行项目总结和反思 …
阅读更多...
【Amazon】安装Cloudwatch代理监控EC2

【Amazon】安装Cloudwatch代理监控EC2

文章目录 一、实验概要二、实验操作步骤2.1 创建 CloudWatch 代理运行角色2.2 安装 CloudWatch 代理软件包2.3 使用 CloudWatch代理收集指标2.4 CloudWatch指标收集确认 三、参考链接 一、实验概要 使用 CloudWatch 代理从 Amazon EC2 实例和本地服务器中收集指标、日志和跟踪信…
阅读更多...
NetSuite 应用性能管理器（APM）

NetSuite 应用性能管理器（APM）

前段时间&#xff0c;我们发过一个文章谈系统健康检查。 NetSuite ERP系统健康检查-CSDN博客文章浏览阅读119次。“健康检查”本质上是属于信息化持续改善的组成部分。如果说信息化是一个持续不断的过程的话&#xff0c;那么“健康检查”就是持续不断的PDCA中的Check那一环。h…
阅读更多...
pygame加载图像，并让小球做平抛运动

pygame加载图像，并让小球做平抛运动

文章目录 load转换和存储自由落体 在游戏设计中&#xff0c;图像显示是必不可少的功能&#xff0c;pygame中的image模块便用于加载图像。 load 通过load函数&#xff0c;可以加载多种图像格式&#xff0c;如下表所示 旧版本bmp, gpeg, png, pcx, tiff, xpmc, lbm(以及pbm, p…
阅读更多...
CountDownLatch实战应用——批量数据多线程协调异步处理(主线程执行事务回滚)

CountDownLatch实战应用——批量数据多线程协调异步处理(主线程执行事务回滚)

&#x1f60a; 作者&#xff1a; 一恍过去 &#x1f496; 主页&#xff1a; https://blog.csdn.net/zhuocailing3390 &#x1f38a; 社区&#xff1a; Java技术栈交流 &#x1f389; 主题&#xff1a; CountDownLatch实战应用——批量数据多线程协调异步处理(主线程执行事务…
阅读更多...
MIT 6.824 -- MapReduce Lab

MIT 6.824 -- MapReduce Lab

MIT 6.824 -- MapReduce Lab 环境准备实验背景实验要求测试说明流程说明 实验实现GoLand 配置代码实现对象介绍协调器启动工作线程启动Map阶段分配任务执行任务 Reduce 阶段分配任务执行任务 终止阶段 崩溃恢复 注意事项并发安全文件转换golang 知识点 测试 环境准备 从官方gi…
阅读更多...
nginx配置文件的简单结构

nginx配置文件的简单结构

nginx的配置文件&#xff08;nginx.conf&#xff09;整体上可分为三个部分&#xff1a;全局块、events块、http块 区域职责全局块配置和nginx运行相关的全局配置events块配置和网络连接相关的配置http块配置代理、缓存、日志记录、虚拟主机等配置在http块中&#xff0c;可以包含…
阅读更多...
Linux的基本指令（四）

Linux的基本指令（四）

目录 前言 时间相关的指令 date指令 时间戳 日志 时间戳转化为具体的时间 cal指令 find指令&#xff08;十分重要&#xff09; grep指令&#xff08;行文本过滤工具&#xff09; 学前补充 什么是打包和压缩&#xff1f; 为什么要打包和压缩&#xff1f; 怎么打包和…
阅读更多...
【洛谷算法题】P5715-三位数排序【入门2分支结构】

【洛谷算法题】P5715-三位数排序【入门2分支结构】

&#x1f468;‍&#x1f4bb;博客主页&#xff1a;花无缺 欢迎 点赞&#x1f44d; 收藏⭐ 留言&#x1f4dd; 加关注✅! 本文由 花无缺 原创 收录于专栏 【洛谷算法题】 文章目录 【洛谷算法题】P5715-三位数排序【入门2分支结构】&#x1f30f;题目描述&#x1f30f;输入格式…
阅读更多...
基于OGG实现MySQL实时同步

基于OGG实现MySQL实时同步

&#x1f4e2;&#x1f4e2;&#x1f4e2;&#x1f4e3;&#x1f4e3;&#x1f4e3; 哈喽&#xff01;大家好&#xff0c;我是【IT邦德】&#xff0c;江湖人称jeames007&#xff0c;10余年DBA及大数据工作经验 一位上进心十足的【大数据领域博主】&#xff01;&#x1f61c;&am…
阅读更多...
常见树种（贵州省）：020女贞、异叶梁王茶、掌叶梁王茶、鹅掌柴、楤木、柞木、华重阳木、马蹄荷、山桐子、刺楸

常见树种（贵州省）：020女贞、异叶梁王茶、掌叶梁王茶、鹅掌柴、楤木、柞木、华重阳木、马蹄荷、山桐子、刺楸

摘要&#xff1a;本专栏树种介绍图片来源于PPBC中国植物图像库&#xff08;下附网址&#xff09;&#xff0c;本文整理仅做交流学习使用&#xff0c;同时便于查找&#xff0c;如有侵权请联系删除。 图片网址&#xff1a;PPBC中国植物图像库——最大的植物分类图片库 一、女贞 …
阅读更多...
我的创作纪念日-五周年

我的创作纪念日-五周年

机缘 5年前&#xff0c;作为一名技术人员&#xff0c;平时利用CSDN作为学习平台工具&#xff0c;帮助解决工作中遇到的问题。随着30、35中年危机渐行渐近&#xff0c;回过头来发现平时虽然也有记录整理学习笔记的习惯&#xff0c;但还没有一个可以持续鞭笞自己和记录自己学习的…
阅读更多...
C#，数值计算——插值和外推，RBF_fn 与 RBF_gauss 的计算方法与源程序

C#，数值计算——插值和外推，RBF_fn 与 RBF_gauss 的计算方法与源程序

1 文本格式 using System; namespace Legalsoft.Truffer { public interface RBF_fn { double rbf(double r); } } ---------------------------------------------- using System; namespace Legalsoft.Truffer { public class RBF_gauss : RBF…
阅读更多...
transformers pipeline出现ConnectionResetError的解决方案

transformers pipeline出现ConnectionResetError的解决方案

大家好，我是爱编程的喵喵。双985硕士毕业，现担任全栈工程师一职，热衷于将数据思维应用到工作与生活中。从事机器学习以及相关的前后端开发工作。曾在阿里云、科大讯飞、CCF等比赛获得多次Top名次。现为CSDN博客专家、人工智能领域优质创作者。喜欢通过博客创作的方式对所学的…
阅读更多...
上海亚商投顾：北证50指数大涨 逾百只北交所个股涨超10%

上海亚商投顾：北证50指数大涨 逾百只北交所个股涨超10%

上海亚商投顾前言&#xff1a;无惧大盘涨跌&#xff0c;解密龙虎榜资金&#xff0c;跟踪一线游资和机构资金动向&#xff0c;识别短期热点和强势个股。 一.市场情绪 沪指11月24日震荡调整&#xff0c;深成指、创业板指盘中跌超1%。北证50指数大涨超6%&#xff0c;北交所个股持…
阅读更多...
[架构之路-253]：目标系统 - 设计方法 - 软件工程 - 软件设计 - 结构化设计的主要评估指标：高内聚（模块内部）、低耦合（模块之间）的含义

[架构之路-253]：目标系统 - 设计方法 - 软件工程 - 软件设计 - 结构化设计的主要评估指标：高内聚（模块内部）、低耦合（模块之间）的含义

目录 前言&#xff1a; 一、软件工程中的软件设计种类&#xff1a;根据宏观到微观分 &#xff08;1&#xff09;软件架构设计&#xff08;层次划分、模块划分、职责分工&#xff09;&#xff1a; &#xff08;2&#xff09;软件高层设计、概要设计&#xff08;功能模块的接…
阅读更多...
[设计模式] 常见的设计模式

[设计模式] 常见的设计模式

文章目录 设计模式的 6 大设计原则设计模式的三大分类常见的设计模式有哪几种1. 单例模式&#xff1a;保证一个类仅有一个实例&#xff0c;并提供一个访问它的全局访问点。&#xff08;连接池&#xff09;1. 饿汉式2. 懒汉式3. 双重检测 2. 工厂模式3. 观察者模式● 推模型● 拉…
阅读更多...
Windows上常用的dos命令

Windows上常用的dos命令

cd更改目录 cd c:\users从其他目录改成c:\users。 type显示文件内容 type good.txt显示文件good.txt里边的内容。 del删除文件 del good.txt删除文件。
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023