混淆矩阵Confusion Matrix
混淆矩阵定义
混淆矩阵是机器学习中总结分类模型预测结果的情形分析表,以矩阵形式将数据集中的记录按照真实的类别与分类模型预测的类别判断两个标准进行汇总。其中矩阵的行表示真实值,矩阵的列表示预测值,下面我们先以二分类为例,看下矩阵表现形式,如下:
| 预测/真实 | 1(Postive) | 0(Negative) |
|---|---|---|
| 1 (Postive) | TP(True Postive:真阳) | FP (False Postive:假阳) |
| 0(Negative) | FN (False Negative:假阴) | TN (True Negative:真阴) |
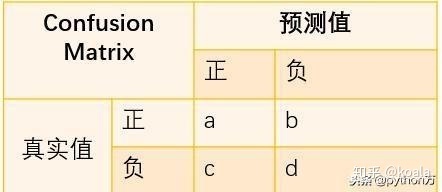
在讲矩阵之前,我们先复习下之前在讲分类评估指标中定义的一些符号含义,如下:
- TP(True Positive):将正类预测为正类数,真实为0,预测也为0
- FN(False Negative):将正类预测为负类数,真实为0,预测为1
- FP(False Positive):将负类预测为正类数, 真实为1,预测为0
- TN(True Negative):将负类预测为负类数,真实为1,预测也为1
刚才分析的是二分类问题,那么对于多分类问题,混淆矩阵表示的含义也基本相同,这里我们以三类问题为例,看看如何根据混淆矩阵计算各指标值。
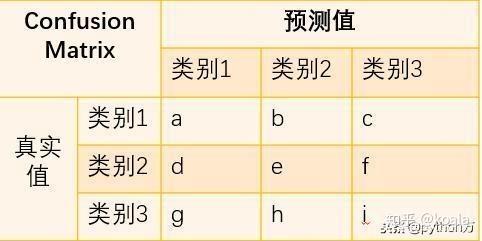
与二分类混淆矩阵一样,矩阵行数据相加是真实值类别数,列数据相加是分类后的类别数,那么相应的就有以下计算公式;
- 精确率_类别1=a/(a+d+g)
- 召回率_类别1=a/(a+b+c)
python 实现混淆矩阵
混淆矩阵(Confusion Matrix),是一种在深度学习中常用的辅助工具,可以让你直观地了解你的模型在哪一类样本里面表现得不是很好。
示例代码一如下:
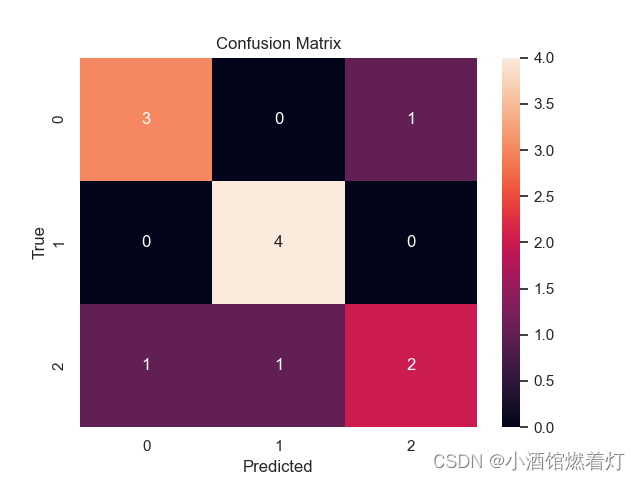
import seaborn as sns
from sklearn.metrics import confusion_matrix
import matplotlib.pyplot as plt
# 使用 seaborn 风格设置
sns.set()
# 创建混淆矩阵
C2 = confusion_matrix([0, 1, 2, 0, 1, 2, 0, 2, 2, 0, 1, 1], [0, 1, 1, 2, 1, 0, 0, 2, 2, 0, 1, 1])
# 创建子图
f, ax = plt.subplots()
# 打印混淆矩阵
print(C2)
# 绘制热力图
sns.heatmap(C2, annot=True, ax=ax)
# 设置标题和轴标签
ax.set_title('Confusion Matrix') # 标题
ax.set_xlabel('Predicted') # x轴
ax.set_ylabel('True') # y轴
# 显示图像
plt.show()
示例代码二如下:
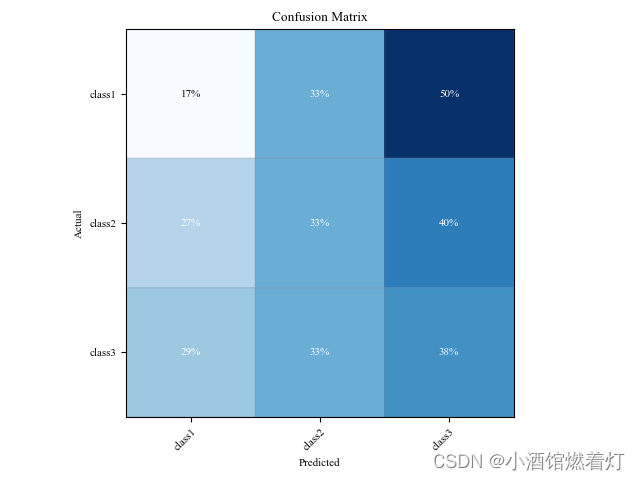
import matplotlib.pyplot as plt
import numpy as np
def plot_Matrix(cm, classes, title=None, cmap=plt.cm.Blues):
plt.rc('font', family='Times New Roman', size='8') # 设置字体样式、大小
# 按行进行归一化
cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
print("Normalized confusion matrix")
str_cm = cm.astype(np.str).tolist()
for row in str_cm:
print('\t'.join(row))
# 占比1%以下的单元格,设为0,防止在最后的颜色中体现出来
for i in range(cm.shape[0]):
for j in range(cm.shape[1]):
if int(cm[i, j] * 100 + 0.5) == 0:
cm[i, j] = 0
fig, ax = plt.subplots()
im = ax.imshow(cm, interpolation='nearest', cmap=cmap)
# ax.figure.colorbar(im, ax=ax) # 侧边的颜色条带
ax.set(xticks=np.arange(cm.shape[1]),
yticks=np.arange(cm.shape[0]),
xticklabels=classes, yticklabels=classes,
title=title,
ylabel='Actual',
xlabel='Predicted')
# 通过绘制格网,模拟每个单元格的边框
ax.set_xticks(np.arange(cm.shape[1] + 1) - .5, minor=True)
ax.set_yticks(np.arange(cm.shape[0] + 1) - .5, minor=True)
ax.grid(which="minor", color="gray", linestyle='-', linewidth=0.2)
ax.tick_params(which="minor", bottom=False, left=False)
# 将x轴上的lables旋转45度
plt.setp(ax.get_xticklabels(), rotation=45, ha="right",
rotation_mode="anchor")
# 标注百分比信息
fmt = 'd'
thresh = cm.max() / 2.
for i in range(cm.shape[0]):
for j in range(cm.shape[1]):
if int(cm[i, j] * 100 + 0.5) > 0:
ax.text(j, i, format(int(cm[i, j] * 100 + 0.5), fmt) + '%',
ha="center", va="center",
color="white" if cm[i, j] > thresh else "black")
fig.tight_layout()
plt.savefig('cm.jpg', dpi=300)
plt.show()
# 构造一个混淆矩阵
cm = np.array([[10, 20, 30], [40, 50, 60], [70, 80, 90]])
classes = ['class1', 'class2', 'class3']
# 调用函数绘制混淆矩阵
plot_Matrix(cm, classes, title='Confusion Matrix')
PR曲线 & AP
Recall召回率(查全率):
R e c a l l = T P T P + F N Recall=\frac{TP}{TP+FN} Recall=TP+FNTP
含义:TP除以第一列,即预测为1实际为1的样本在所有真实为1类别中的占比。
Presession精准率(查准率):
P r e s e s s i o n = T P T P + F P Presession=\frac{TP}{TP+FP} Presession=TP+FPTP
含义:FP除以第一行,即预测为1实际为1的样本在所有预测为1类别中的占比。
PR曲线:
同理ROC曲线。在模型预测的时候,我们输出的预测结果是一堆[0,1]之间的数值,怎么把数值变成二分类?设置一个阈值,大于这个阈值的值分类为1,小于这个阈值的值分类为0。ROC曲线就是我们从[0,1]设置一堆阈值,每个阈值得到一个(Presession,Recall)对,纵轴为Presession,横轴为Recall,把所有的(Presession,Recall)对对连起来就得到了PR曲线。
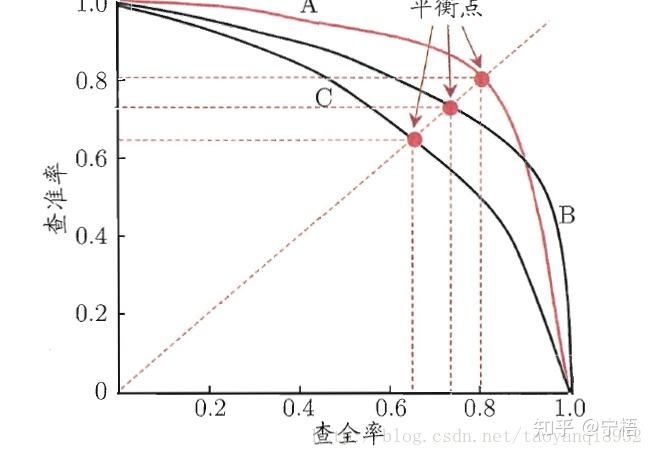
AP(PR曲线下的面积):
跟TPR和FPR不一样的是,在PR关系中,是一个此消彼长的关系,但往往我们希望二者都是越高越好,所以PR曲线是右上凸效果越好(也有例外,有比如在风险场景当预测为1实际为0时需要赔付时,大致会要求Recall接近100%,可以损失Precision)。所以除了特殊情况,通常情况都会使用Precision-recall曲线,来寻找分类器在Precision与Recall之间的权衡。
AP就是Precision-recall 曲线下面的面积,通常来说一个越好的分类器,AP值越高。
还有一个mAP的概念,mAP是多个类别AP的平均值。这个mean的意思是对每个类的AP再求平均,得到的就是mAP的值,mAP的大小一定在[0,1]区间,越大越好。该指标是目标检测算法中最重要的一个。
精准率和召回率是相互制约的,如果想要精准率提高,召回率则会下降,如果要召回率提高,精准率则会下降,我们需要找到二者之间的一个平衡。
P-R曲线的生成方法:根据学习器的预测结果对样本进行排序,排在前面的是学习器认为最可能是正例的样本,排在最后的是最不可能是正例的样本,按此顺序逐个将样本作为正例预测,则每次可以计算出当前的查全率、查准率,以查全率为横轴、查准率为纵轴做图,得到的查准率-查全率曲线即为P-R曲线。也就是说对每个样本预测其为正例的概率,然后将所有样本按预测的概率进行排序,然后依次将排序后的样本做为正例进行预测,从而得到每次预测的查全率与查准率。这个依次将样本做为正例的过程实际上就是逐步降低样本为正例的概率的域值,通过降低域值,更多的样本会被预测为正例,从而会提高查全率,相对的查准率可能降低,而随着后面负样本的增加,查全率提高缓慢甚至没有提升,精度降低会更快。
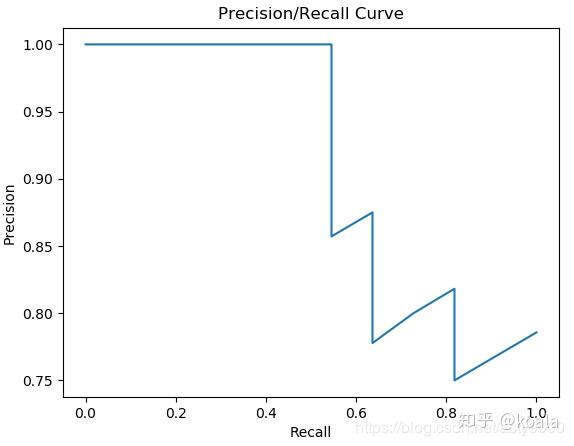
代码实现如下:
import matplotlib.pyplot as plt
from sklearn.metrics import precision_recall_curve
import numpy as np
plt.figure('P-R Curve')
plt.title('Precision/Recall Curve')
plt.xlabel('Recall')
plt.ylabel('Precision')
#y_true为样本实际的类别,y_scores为样本为正例的概率
y_true = np.array([1, 1, 1, 1, 1, 0, 1, 1, 0, 1, 1, 1, 0, 0, 0, 0, 1, 0, 0, 0])
y_scores = np.array([0.9, 0.75, 0.86, 0.47, 0.55, 0.56, 0.74, 0.62, 0.5, 0.86, 0.8, 0.47, 0.44, 0.67, 0.43, 0.4, 0.52, 0.4, 0.35, 0.1])
precision, recall, thresholds = precision_recall_curve(y_true, y_scores)
plt.plot(recall,precision)
plt.show()
ROC曲线 & AUC
真阳率:
T P R = T P T P + F N = F P P TPR=\frac{TP}{TP+FN}=\frac{FP}{P} TPR=TP+FNTP=PFP
含义:TP除以第一列,即预测为1实际为1的样本在所有真实1类别中的占比。
假阳率:
F P R = F P F P + T N = F P N FPR=\frac{FP}{FP+TN}=\frac{FP}{N} FPR=FP+TNFP=NFP
含义:FP除以第二列,即预测为1实际为0的样本在所有真实0类别中的占比。
ROC曲线:
在模型预测的时候,我们输出的预测结果是一堆[0,1]之间的数值,怎么把数值变成二分类?设置一个阈值,大于这个阈值的值分类为1,小于这个阈值的值分类为0。ROC曲线就是我们从[0,1]设置一堆阈值,每个阈值得到一个(TPR,FPR)对,纵轴为TPR,横轴为FPR,把所有的(TPR,FPR)对连起来就得到了ROC曲线。
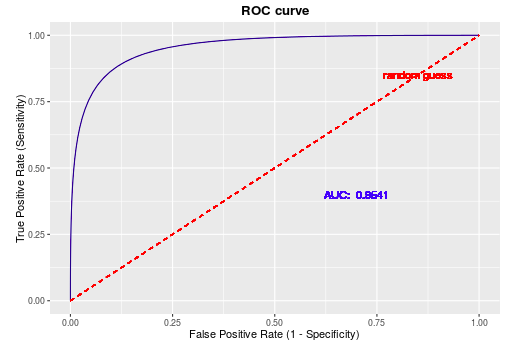
代码实现:
import matplotlib
import numpy as np
import matplotlib.pyplot as plt
from sklearn.metrics import precision_recall_curve, roc_curve
plt.figure()
plt.title('PR Curve')
plt.xlabel('Recall')
plt.ylabel('Precision')
plt.grid()
# 只是理解两种曲线的含义,所以数据简单的构造
confidence_scores = np.array([0.9, 0.46, 0.78, 0.37, 0.6, 0.4, 0.2, 0.16])
confidence_scores = sorted(confidence_scores, reverse=True) # 置信度从大到小排列
print(confidence_scores)
data_labels = np.array([1, 1, 0, 1, 0, 0, 1, 1]) # 置信度所对应的标签
# 精确率,召回率,阈值
precision, recall, thresholds = precision_recall_curve(data_labels, confidence_scores)
print(precision)
print(recall)
print(thresholds)
plt.plot(recall, precision)
plt.show()
# 真正率,假正率
fpr, tpr, thresholds = roc_curve(data_labels, confidence_scores)
# print(fpr)
# print(tpr)
plt.figure()
plt.grid()
plt.title('Roc Curve')
plt.xlabel('FPR')
plt.ylabel('TPR')
from sklearn.metrics import auc
auc = auc(fpr, tpr) # AUC计算
plt.plot(fpr, tpr, label='roc_curve(AUC=%0.2f)' % auc)
plt.legend()
plt.show()
AUC(area under the curve):
(1)计算方法一
AUC即ROC曲线下的面积。曲线越靠近左上角,意味着TPR>FPR,模型的整体表现也就越好。所以我们可以断言,ROC曲线下的面积越大,模型效果越好。
最坏的情况是,总是有TPR=FPR,如下图,表示对于不论真实类别是1还是0的样本,分类器预测为1的概率是相等的。换句话说,分类器对于正例和负例毫无区分能力。如果AUC小于0.5,那么只要把预测类别取反,便得到了一个AUC大于0.5的分类器。
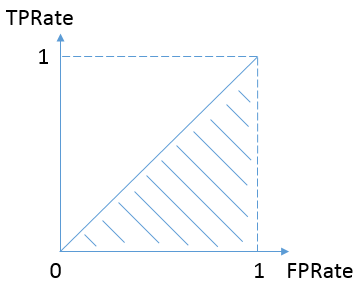
(2)计算方法二
AUC还有一种解释就是任取一对正负样本,正样本的预测值大于负样本的预测值的概率。 显然可以写出计算AUC伪代码为:
1.统计所有正样本个数P,负样本个数N;
2.遍历所有正负样本对,统计正样本预测值大于负样本预测值的样本总个数number
3. A U C = n u m b e r / ( P ∗ N ) AUC = number / (P * N) AUC=number/(P∗N) 一些计算细节是当正负样本预测值刚好相等时,该样本记为0.5个。
PS: 在实际代码实现过程中其实可以和第一种方法一样进一步优化,可以先对正负样本排序,利用dp的思想迭代计算个数,可以将复杂度从 O ( N 2 ) O(N^2) O(N2)降低为 O ( N l o g N ) O(NlogN) O(NlogN)。
类别不平衡问题中如何选择PR与ROC
这里特指负样本数量远大于正样本时,在这类问题中,我们往往更关注正样本是否被正确分类,即TP的值。PR曲线更适合度量类别不平衡问题中:
- 因为在PR曲线中TPR和FPR的计算都会关注TP,PR曲线对正样本更敏感。
- 而ROC曲线正样本和负样本一视同仁,在类别不平衡时ROC曲线往往会给出一个乐观的结果。
理解的动态图:
https://zhuanlan.zhihu.com/p/92218196
![[网络] 5. TCP 链接的建立与释放~汇总](https://img-blog.csdnimg.cn/8365c28011be4da49e966379f20fd90f.png)








![[计算机网络]应用层概述](https://img-blog.csdnimg.cn/2fc98d4075304cf2820ae24f2f9fb69d.png)