前言

相信大家对于谷歌RateLimiter一定并不陌生,在项目中应该也经常拿来进行限流，但是对于其实现原理并不一定能用熟于心，本文带大家从源码探究RateLimiter的设计与具体实现。

RateLimiter的组成

从源码可以看到，RateLimiter由stopwatch与mutexDoNotUseDirectly组成，先简单了解其分别的作用如下：

• stopwatch：计时器的作用.
• mutexDoNotUseDirectly：主要通过锁解决并发问题，本文暂不叙述此块，感兴趣的同学可以留言。

源码分析

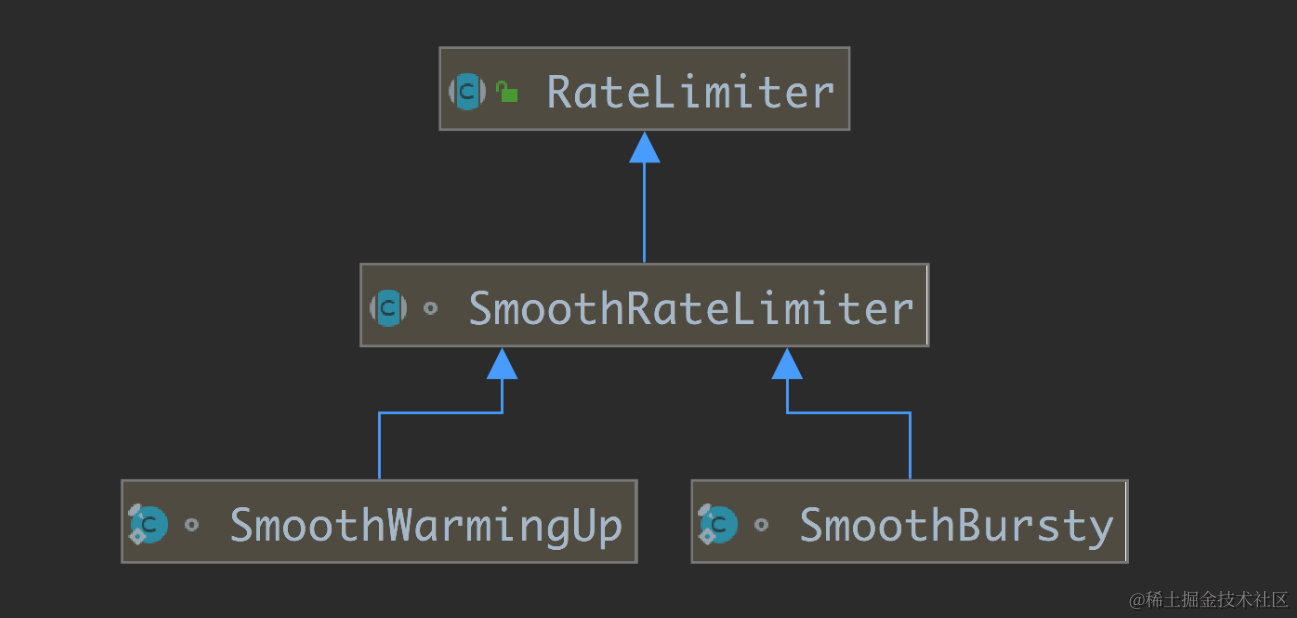
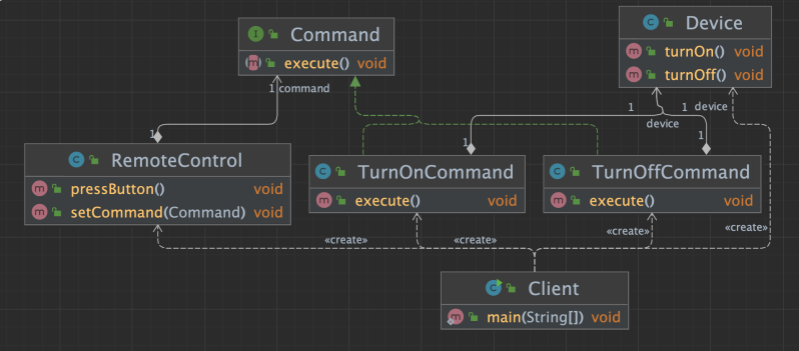
上图展示了RateLimite的类图，可以看到其有一个子类SmoothRateLimiter，在往下看SmoothRateLimiter中有两个实现类SmoothBursty与SmoothWarmingUp，分别表示两种限流的不同场景，SmoothBursty是我们常见的关于限流算法中令牌桶算法的一个实现，通过固定速率生成令牌，当流量进入时，申请令牌，令牌充足时则直接获取成功，不充足时返回等待时间，而SmoothWarmingUp与SmoothBursty不同的是，SmoothWarmingUp在固定速度的基础上增加了预热流程，可以更好的应对突发流量。 另外，在初始化和小流量时更慢得进行流量得提供也符合实际的应用场景，本文主要讲述常用SmoothBursty的实现。

为了便于理解，我们从最简单限流程序开始一步一部理解RateLimiter的设计与实现。

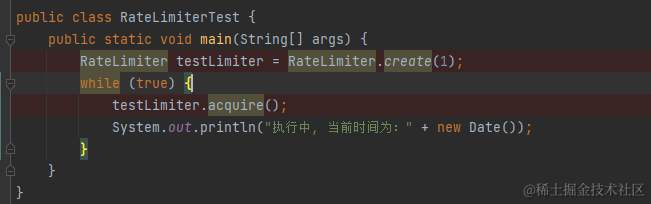
1.RateLimiter创建

可以看到，RateLimiter创建分为两步，首先创建RateLimiter的实现类SmoothBursty对象，然后setRate设置限流器的控制速率。
首先我们看下SmoothBursty的实现，其首先创建了SleepingStopwatch类stopwatch对象。

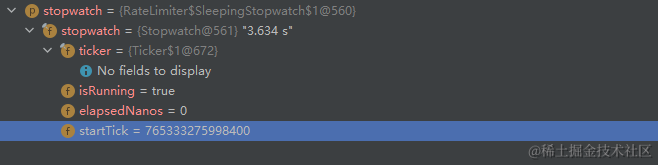
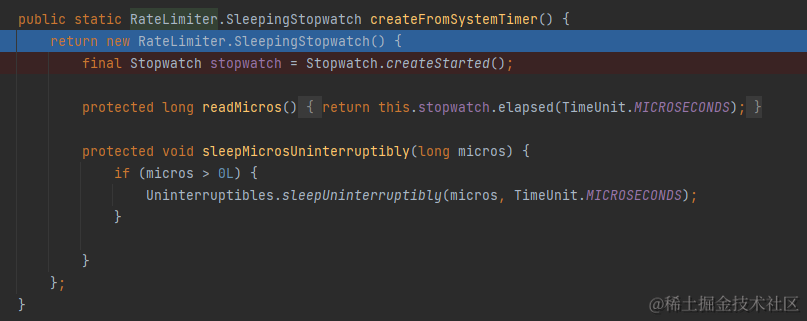
stopwatch中初始elapsedNanos = 0 startTick = 765333275998400,其有一个sleepMicrosUninterruptibly方法,释义如下

• elapsedNanos：经过的时间，单位为纳秒
• startTick：开始时间
• sleepMicrosUninterruptibly(long micros)：实现了不可中断的不可中断的sleep(用于令牌不足时限流等待)

紧接着其传入stopwatch与maxBurstSeconds创建一个SmoothBursty对象，SmoothBursty继承至SmoothRateLimiter，其额外定义了一个maxBurstSeconds变量，SmoothRateLimiter继承至RateLimiter，是RateLimiter抽象类的具体实现，其中有四个变量我们同maxBurstSeconds一起进行解释：

• SmoothRateLimiter.storedPermits：实际预存的许可(即令牌)
• SmoothRateLimiter.maxPermits：最大的许可数(即令牌)
• SmoothRateLimiter.stableIntervalMicros：每产生一个令牌需要消耗的微秒数
• SmoothRateLimiter.nextFreeTicketMicros：初始值为0L，表示下一个令牌可用的时间戳
• SmoothBursty.maxBurstSeconds：初始值为1.0D，表示桶中最多可以保存多少秒存入的令牌数

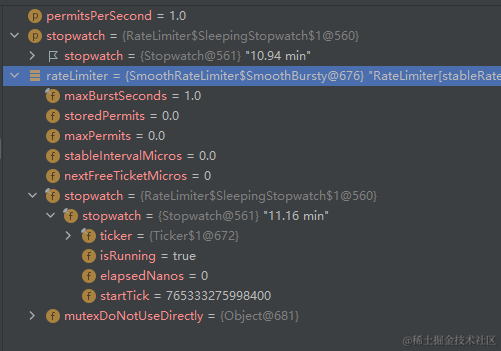
从上图可以看到RateLimiter创建后，开始setRate传入的permitsPerSecond设置限流速率

• permitsPerSecond:令牌数/每秒钟，即我们期望限制的qps.

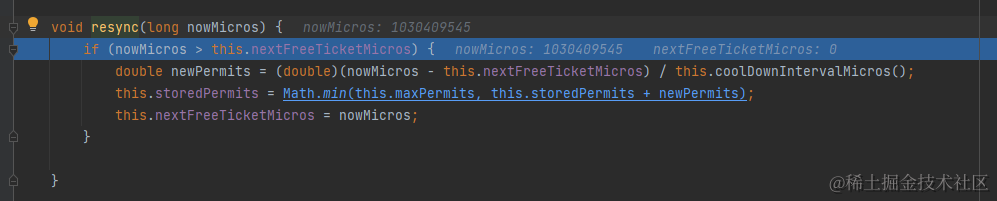
传入的nowMicros当前值为1030409545，nextFreeTicketMicros初始为0，此步骤计算赋值了当前存储的令牌数量storedPermits与
nextFreeTicketMicros = nowMicros(1030409545)；

然后根据传入的permitsPerSecond设置了产生一枚令牌需要的时间：stableIntervalMicros。

接着起开始按比例更新当前存储的令牌数量，可以看到，初始令牌数量为0时，其首次创建时存储的令牌数量即为0.0, maxPermits = maxBurstSeconds * permitsPerSecond = 1.0
至此RateLimiter的初始创建结束，下面我们从最简单也是日常使用最多的方法acquire()看看其如何通过上述各个变量控制限流。为了方便理解，下图展示了，当前RateLimiter的组成。

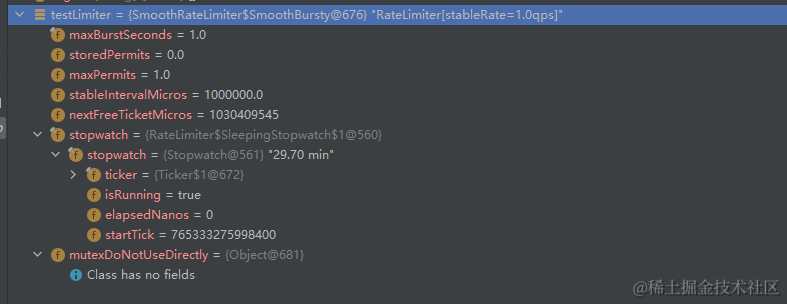
2.RateLimiter.acquire()控制限流

还是从源码入手，可以看到acquire()实际调用的方法acquire(1)，即当前需要获取1块令牌，其实现分为3个步骤

1. 计算需要等待的时间microsToWait
2. stopwatch.sleepMicrosUninterruptibly(microsToWait)进行阻塞等待。
3. 返回等待时间
   从第1步开始看，传入令牌数与当前时间nowMicros = 2322440641 由于当前令牌数量足够计算出momentAvailable = 0，即无需阻塞等待，

且将nextFreeTicketMicro等于当前时间nowMicros后，则可以推测出下次计算时nowMicros必然大于nextFreeTicketMicros，此时无需等待。

这是因为nowMicros > nextFreeTicketMicros 时，此间产生令牌数量 + 当前持有的令牌数量 一定大于 最大的令牌数量，而最大的令牌数量大于请求的令牌数量，所以请求无需限流阻塞等待。

而当并发请求数变多，导致某一时刻持有的令牌数量不足时，则会发生限流阻塞等待，为了方便分析，我们通过限流设置为1qps,通过单词请求1000000000个令牌数模拟高并发场景。

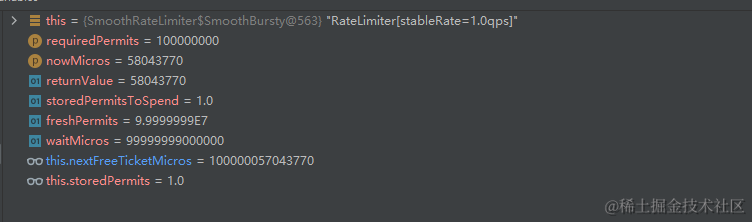
可以看到初次请求时，nowMicros > nextFreeTicketMicros满足，此时令牌数量为1，而超过的令牌数量为refreshPermits = 99999999，通过计算，需要99999999000000的间隔时间才能产生这么多令牌，而此时注意了，返回值为上一次(这里初始请求的上一次即初始值为0)的nextFreeTicketMicros = 0，然后将本次请求的nextFreeTicketMicros增加99999999000000，而最终计算出的等待时间为Math.max(momentAvailable - nowMicros, 0L) = 0.实际并没有产生等待，而在下一次请求时，如下图可以看到此时nowMicros < nextFreeTicketMicros, 此时说明还未到令牌释放的时间，需要等待Math.max(momentAvailable - nowMicros, 0L) = 0, 可以看到本次请求等待的时间，其实时上次请求时超出的令牌数需要等待的时间，继续往下执行你就会发现，RateLimiter每次请求的超支的令牌等待时间，都是在下一次执行时进行等待。

结语

SmoothBrusty的设计遵循令牌桶的思路，SmoothBursty以指定的速率生成许可，当一个请求申请获取许可时，如果当前许可数满足申请数量，则消耗掉许可，直接返回无需等待。当当前许可数小于申请数量时，会计算多余部分许可需要等待生成的时间，更新下一次许可可发放的时间，但值得注意的是尽管已经消耗掉所有的许可并且不够总请求数量，本次请求也并不会阻塞等待，而是将阻塞等待放到下一个请求，说明此处可以支持突发流量。这里的设计其实还是蛮巧妙的。比如一些突发流量场景，当前瞬发的高流量请求可快速返回，无需阻塞，而后续请求可能相隔很久，则请求时不会等待，从而提高系统整体的响应速率，当然这在某些场景可能会导致qps超标，存在造成系统崩溃风险，这里我们主要了解其设计原理，放才能在合适场景合理使用以及规避风险。