目录

一、PR图、BEP

1.PR图

2.BEP 

二、灵敏度、特异度

1.灵敏度

2.特异度

三、真正率、假正率 

1.真正率

2.假正率 

三、ROC、AUC

1.ROC

2.AUC

四、KS值

---

一、PR图、BEP

1.PR图

二分类问题模型通常输出的是一个概率值，我们需要设定一个阈值，让大于这个阈值的时候为正样本，其余的为负样本。

如果我们选择不同的阈值，我们就可以得到不同的预测结果，也就可以得到不同的混淆矩阵，从而得到不同的precision值和recall值。P-R图是我们在连续变化的阈值下，得到的准确率和召回率的关系。（召回率作为横轴，将精确率作为纵轴）。

PR 图主要有以下用途：

1. 权衡 Precision 和 Recall： PR 图帮助我们直观地理解在不同阈值下模型的 Precision 和 Recall 的权衡关系。这对于某些应用中 Precision 和 Recall 之间存在权衡关系的情况非常重要，例如在医学领域的疾病诊断中，我们可能更关注 Recall，以确保尽可能多地捕获患者的真实病情。

2. 评估样本不平衡： 当数据集中的类别不平衡时，PR 图比 ROC 曲线更能准确地反映模型性能。在样本不平衡的情况下，ROC 曲线可能给出过于乐观的评估，而 PR 图更能反映模型在正类别上的性能。

3. 选择适当的阈值： PR 图可以帮助选择适当的分类阈值，以满足特定任务的需求。根据应用场景，我们可能更关注 Precision 或 Recall，通过观察 PR 图可以更好地理解不同阈值下的模型表现。

4. 比较模型性能： PR 图可用于比较不同模型的性能。具体来说，我们可以比较不同模型在保持较高 Precision 的同时实现较高 Recall 的能力，或者根据实际需求调整模型的阈值。

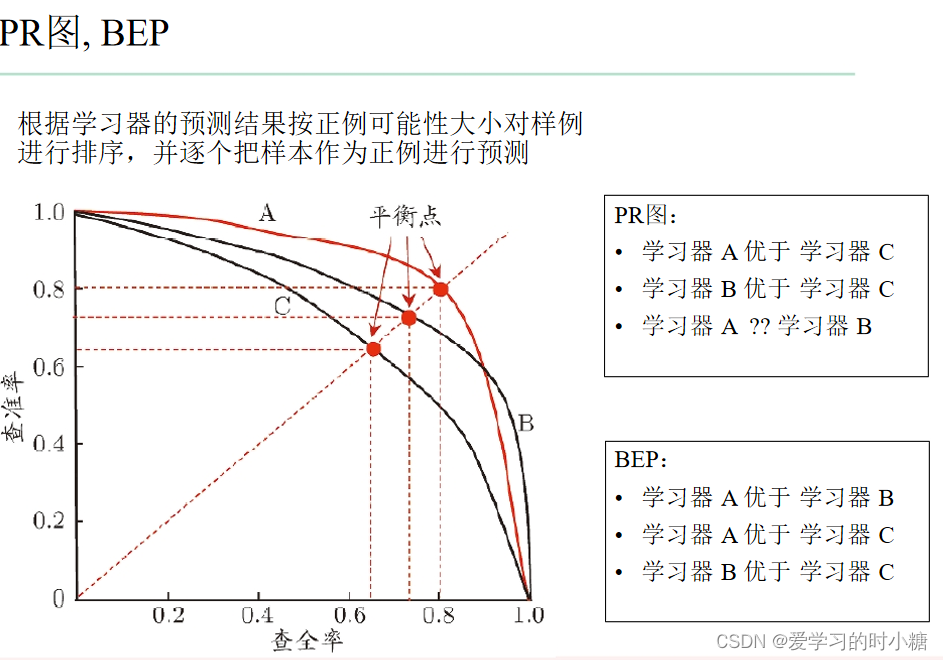
下图A模型的曲线完全包住C模型的曲线，我们就说A模型比C模型的效果好；

B模型的曲线完全包住C模型的曲线，我们就说B模型比C模型的效果好；

但是A模型和B模型的曲线有交叉，我们使用BEP进行比较。

2.BEP 

BEP是精确率和召回率的平衡点，P=R时，那一条线。如果，模型的PR曲线有交叉，我们可以根据BEP来判断模型的好坏。

BEP过于简单，我们常用F1值来比较模型。F1值是考虑了召回率和精确率的一个计算指标。

二、灵敏度、特异度

1.灵敏度

灵敏度的计算公式为：

灵敏度  

灵敏度是在实际的正样本中，能够找到正样本的能力。 它和召回率的公式一样，它就是召回率。

2.特异度

特异度的计算公式为：

特异度   

特异度是指在实际所有的负样本中，找到正确负样本的能力。 

三、真正率、假正率 

1.真正率

真正率=召回率=灵敏度   

真正率的含义是在所有实际的正样本下识别为正样本的概率。

2.假正率 

误判率 = 假正率 = 1 - 特异度 = 

因为特异度是在实际的负样本中找到负样本的能力，1-特异度就代表它在所有实际的负样本中找正样本的能力，那这肯定不对啦，在负样本中怎么能找到正样本呢？所有这些正样本是错误的正样本。所以我们把这个概率也叫做假正率。 

在我们实际工作中，为了避免样本对于精确率和召回率的影响，可以使用TPR和FPR。

三、ROC、AUC

1.ROC

ROC曲线是我们在连续变化的阈值下，生成不同的正负样本，对应出不同的混淆矩阵，得到不同的TPR和FPR值所绘制出来的一条曲线，它表示TPR和FPR的关系。

图中有一条绿色的直线，这条绿的直线代表真正率和假正率概率一样，也就是这种分类概率和我们随机猜的概率一样，模型效果差，不能用。越靠近这条直线，模型效果越差，这条绿色直线下面的是指，绝大多数情况下，模型的正样本都预测错了，根本不能用。

我们希望的是，真正率高，假正率低，也就是靠近左上方（0，1）的位置，此时真正率接近于1，假正率接近于0

2.AUC

AUC是ROC曲线下面的面积，在绿色直线处，总面积1被一分为二，我们需要直线上面部分的面积，这一部分面积的值为0.5-1，小于0.5不能用。

• 0.5 - 0.7：效果较低
• 0.7 - 0.85：效果一般
• 0.85 - 0.95：效果很好
• 0.95 - 1：效果非常好，一般不可能。要对这个结果持怀疑态度，进一步分析模型的准确性。

四、KS值

横坐标为在连续的阈值变化下的正样本的个数（概率分数、模型预测数）。纵坐标为TPR和FPR。

KS为在某一阈值的正样本数（概率分数） 下，TPR-FPR的值。

KS = TPR - FPR

KS用来评估模型好坏样本的区分程度，有时候人们会把0.6的KS值乘以100，说成60，也正确。

• KS<20：欠拟合，模型不具备可用性
• KS>20 & KS<30：模型可用
• KS>30 & KS<40 ：模型预测能力优秀
• KS>40：模型区分度很高。我们需要对这个结果持怀疑态度，进一步分析模型的准确性。

如果模型的AUC或KS值很高，并不是一件好事情。我们要进一步分析模型的准确性，避免是因为数据不准确导致的。

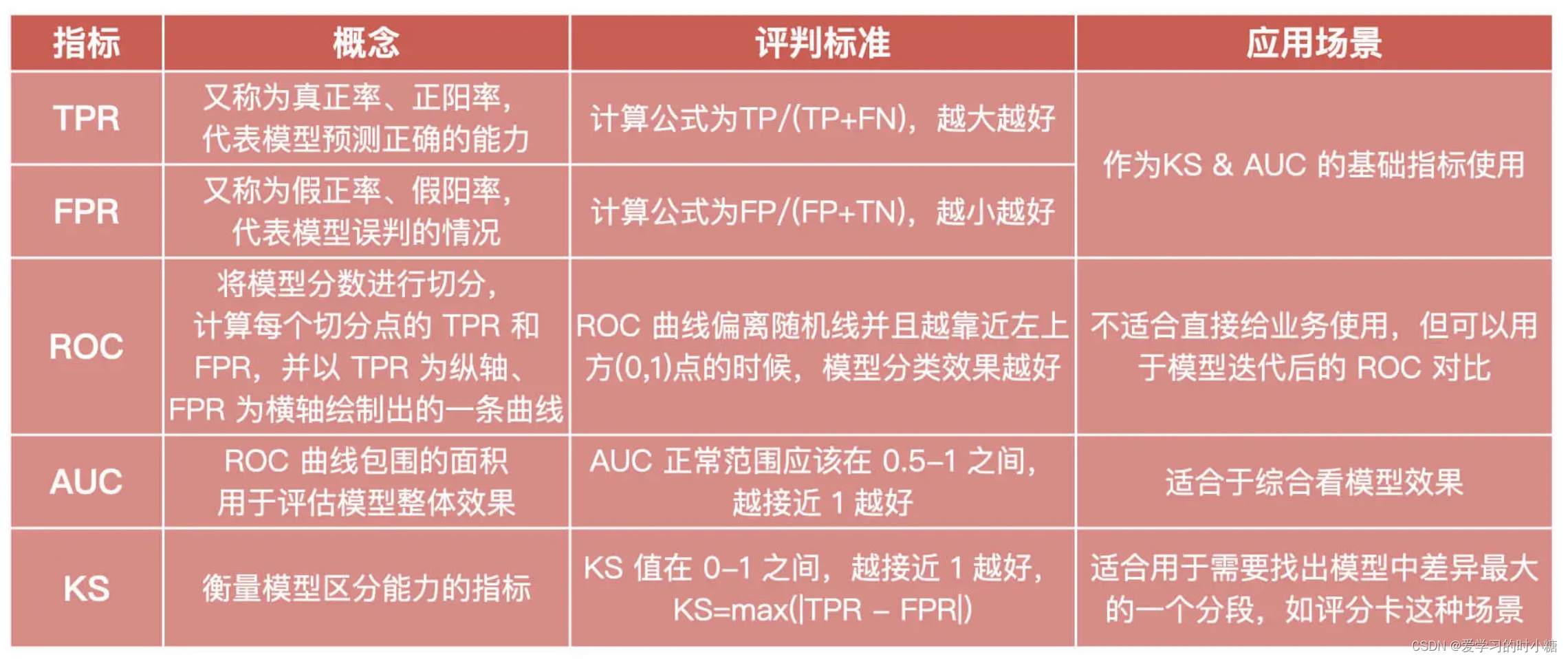
准确率，精准率，召回率，真正率，假正率，ROC/AUC-CSDN博客

参考文献： 刘海丰——《成为AI产品经理》

声明：本文是对于刘海丰老师《成为AI产品经理》课程重点的总结，自用，请勿传播。