1. 文章简介

• 标题：Toolformer: Language Models Can Teach Themselves to Use Tools
• 作者：Timo Schick, Jane Dwivedi-Yu, Roberto Dessì, Roberta Raileanu, Maria Lomeli, Luke Zettlemoyer, Nicola Cancedda, Thomas Scialom
• 日期：2023
• 期刊：arxiv preprint

2. 文章概括

  文章给出了一种可以自动调用API的LLM方法“Toolformer”，该工具可以自行决定是否调用API，何时调用API以及调用什么API，从而达到通过API检索增强增加LLM回答的可靠性。

3 文章重点技术

3.1 Toolformer

  给定语言模型$M$，给定一系列可供调用的API接口$c=(a_c,i_c)$，其中$a_c$为API的名称，$i_c$为API的输入，API会返回结果$r$，记$e(c,r)=<API>a_c(i_c)\to r</API>)$，其中$<API>,</API>,\to$表示特殊token，用于区分API的输入和输出。给定数据集 C = { x 1 , … , x ∣ C ∣ } \mathcal{C} = \{x^1, \dots, x^{|\mathcal{C}|}\} C={x1,…,x∣C∣}，其中$x^i$表示输入的文本。则Toolformer按照如下的步骤进行训练、推理：

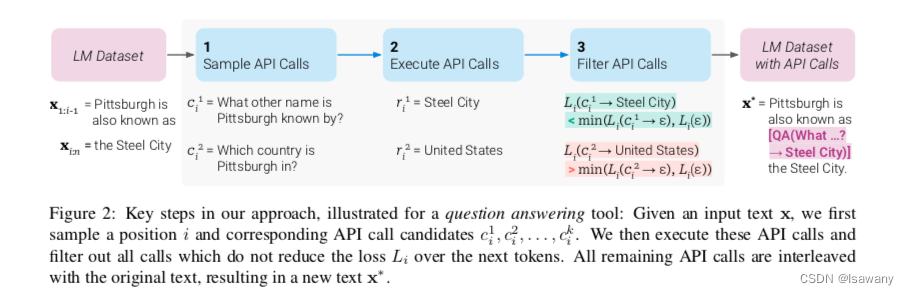
• Sampling API Calls：首先，对每个API接口，我们设计一个对应的prompt“$P(x)$"让模型自动改写原始输入为调用API的输入。如下图所示，对一个原始输入文本$x$，对任意位置 i ∈ { 1 , … , n } i\in\{1, \dots, n\} i∈{1,…,n}，我们基于$x_1,\dots ,x_{i-1},P(x)$预测下一个token是$<API>$的概率$p_i=p_M(<API>|P(x),x_{1:i-1})$，如果条件概率值高于给定阈值${\tau }_s$，则认为模型应该在该位置调用API，如果存在高于$k$个位置的概率值大于${\tau }_s$，则只保留top$k$个位置。最终得到需要调用API的位置集合 I = { i ∣ p i > τ s } I=\{i|p_i > \tau_s\} I={i∣pi​>τs​}(不超过k个)。接下来，对每个$i\in I$，我们基于$[P(x),x_1,\dots ,x_{i-1},<API>]$调用API接口得到接下来的预测结果。
  
• Executing API Calls: 接下来执行上述语言模型自动生成的API调用文本$c_i$，得到对应的结果$r_i$。
• Filtering API Calls：令$$\begin{gathered} L_i(z)=-\sum _{j=i}^n{w}_{j-i}\log p_M(x_j|z,x_{1:j-1}) \\ {L}_i^{+}=L_i(e(c_i,r_i)) \\ {L}_i^{-}=\min (L_i(ϵ),L_i(e(c_i,ϵ))) \end{gathered}$$，其中$ϵ$表示空序列。上述$L_i^{+}$实际表示给定$x_1,\dots ,x_{j-1}$和API返回结果$r_i$，模型预测得到$x_j$的加权概率的负数，$L_i^{-}$表示不进行API访问，或者只进行API访问但是不返回结果的情况下，模型得到$x_j$的最小损失。如果$L_i^{+}$比$L_i^{-}$小很多，则可以认为访问API确实带来了收益。从而我们可以通过设置阈值${\tau }_f$，当$L_i^{-}-L_i^{+}\ge {\tau }_f$时，认为模型应该在$i$位置访问API。
• Model Finetuning：给定文本$x$和位置$i$处的API访问结果$(c_i,r_i)$，我们可重写输入文本为$x_{1:i-1},e(c_i,r_i),x_{i:n}$，最后基于数据集$\mathcal{C}$生成SFT数据集${\mathcal{C}}^{\ast }$。在${\mathcal{C}}^{\ast }$上对模型进行微调，得到我们的toolformer工具。
• Inference：推理阶段，我们进行正常的解码，直至模型生成$\to$特殊token，此时我们将$<API>,\to$之间的文本输入待调用的API，得到结果$r$，然后我们将该结果拼接到模型的解码结果中，并插入$</API>$特殊token进行标记，然后继续解码直至结束。
  

3.2 APIs

  我们选择了多种API对语言模型进行加强：

• 针对问答类型的文本，文章采用问答大模型Atlas作为API进行加强
• 针对数学计算，文章采用一个简单的python工具作为API进行加强
• 针对维基百科搜索，文章采用BM25作为API进行加强
• 针对多语言，文章采用fast-text进行语言检测，然后通过NLLB作为API统一翻译成英文进行加强
• 针对日期类问题，文章直接返回系统当前日期作为API进行加强

4. 文章亮点

  文章提出了Toolformer工具，可通过对数据集进行采样、过滤生成SFT数据集，从而对LM进行微调，得到一个通过访问不同API来对LM能力进行加强对工具。实验表明，文章提出的Toolformer在多个API相关的下游任务上有明显提升，且ppl结果表示模型在自然语言生成任务上的能力并没有降级。

5. 原文传送门

Toolformer: Language Models Can Teach Themselves to Use Tools