本来准备和女儿一起玩一道几何题,想想还是算了,不如讲点更有趣的。
任何因式分解都是在堆积木,不信你看:
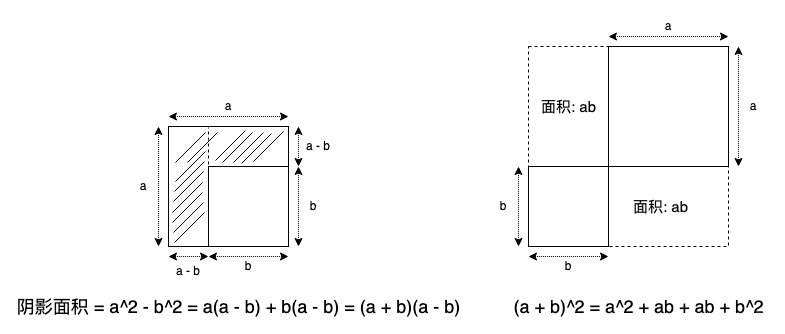
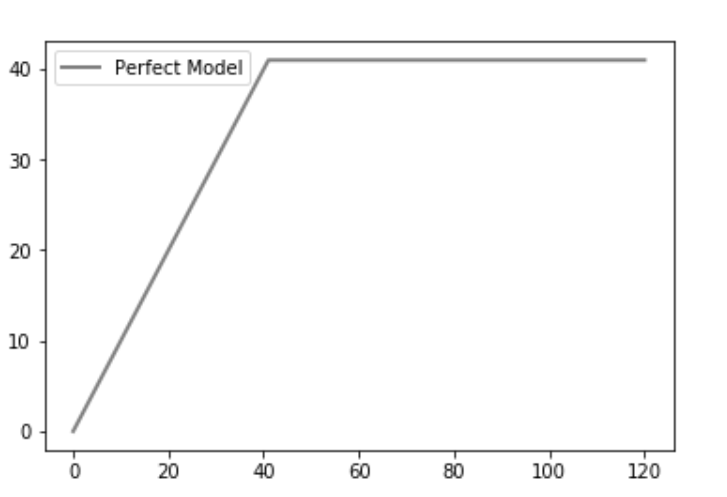
二项式定理,洋灰三角,都是面积,体积,超维体积的拼接,一个大超立方体能够如何 “最优化” 切割成若干小超长方体,比如 3 维立方体,(a + b)^3 = a^3 + 3a^2b + 3ab^2 + b^3,意思就是一个大立方体可以切割成 1 + 3 + 3 + 1 个小长方体,其它切法都比这个麻烦。
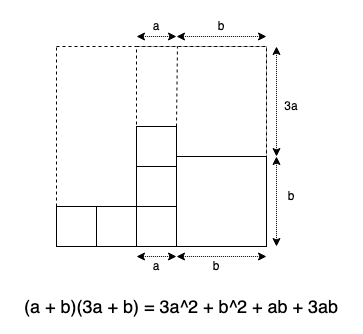
随便摆置,比如 (a + b)(3a + b) 可以看作两个括号内为边的面积,展开后就是一堆小长方形的拼接:
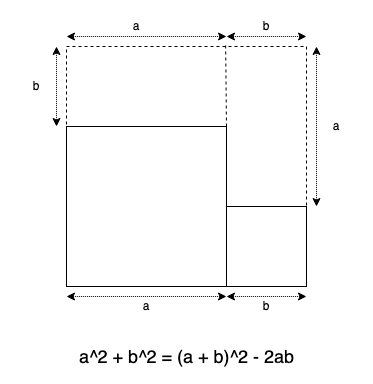
为什么没有平方和公式?其实是有的,只是这样没什么意义而已:
这么极端简单的东西,写这些肯定会被程序员骂 low bi,但我要表达的不是这些个简单因式分解的解法,而是一个方法论,数形结合的思想可以解决几乎任何问题,这个笛卡尔早就说过。
在坐标系里解代数题,微积分大概也是这个意思,连续世界的积累意义,就是面积,而函数则刻画过程的细节。
有点形而上,但几乎就是事实,世界一个瞬间的本身就由 “形态” 组成,不然哪有什么形而上下,而精确描述世界的形态则需要量化,如果可以将世界抽象为几何体,那么描述世界就是求面积,求体积的数学题。
仔细理解古希腊那些学派,大概就是这个意思,世界是 xx 组成的,求的就是个本质。
加入时间维度,一切都可以几何化,譬如说 tcptrace,aimd 收敛图,k 线图,一切随时间变化的变量就和随空间变化的变量一样,最终就是一系列的立方体。
刷抖音时后台如何判断是继续缓存当前视频还是转而缓存下一个视频,因为它是现实的,所以这也是个几何问题:
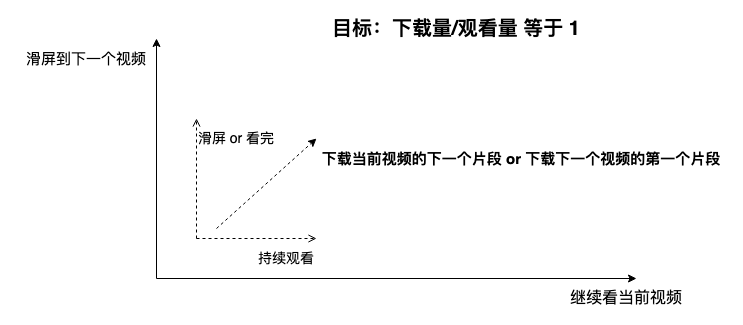
如果我连抖音的运作机制都不懂,我怎么优化传输效率?但我如果不谙世事不善言辞,那我只需要解一道几何题就好了。
我曾跟女儿说,把你遇到的一切都落实到笛卡尔坐标系,你就能卷过所有人。这不是吹牛,大概率是真的。一个不懂通过几何辅助线秀奇技淫巧的智商一般的人,靠笛卡尔坐标系硬算是有可能赢过大师的,这也是为什么我说微积分是科学领域的工业化工具的原因,就像秦弩一样,门槛低,全民列装就扫六合了。
浙江温州皮鞋湿,下雨进水不会胖。