A - Counting Passes
Description
Problem Statement
N
N
N people labeled
1
,
2
,
…
,
N
1,2,\dots,N
1,2,…,N took an exam, and person
i
i
i scored
A
i
A_i
Ai points.
Only those who scored at least
L
L
L points pass this exam.
Determine how many people out of the
N
N
N have passed the exam.
Constraints
All input values are integers.
1
≤
N
≤
100
1 \le N \le 100
1≤N≤100
1
≤
L
≤
1000
1 \le L \le 1000
1≤L≤1000
0
≤
A
i
≤
1000
0 \le A_i \le 1000
0≤Ai≤1000
Input
The input is given from Standard Input in the following format:
N N N L L L
A 1 A_1 A1 A 2 A_2 A2 … \dots … A N A_N AN
Output
Print the answer as an integer.
Sample Input 1
5 60
60 20 100 90 40
Sample Output 1
3
Five people took the exam. You need to score at least
60
60
60 points to pass.
Person
1
1
1 scored
60
60
60 points, so they passed.
Person
2
2
2 scored
20
20
20 points, so they did not pass.
Person
3
3
3 scored
100
100
100 points, so they passed.
Person
4
4
4 scored
90
90
90 points, so they passed.
Person
5
5
5 scored
40
40
40 points, so they did not pass.
From the above, we can see that three people have passed.
Sample Input 2
4 80
79 78 77 76
Sample Output 2
0
There may be cases no one has passed.
Sample Input 3
10 50
31 41 59 26 53 58 97 93 23 84
Sample Output 3
6
Solution
涉及算法:枚举
枚举 N N N 个数,对于每一个数判断是否大于 L L L,如果是,答案加 1 1 1。
Code
#include <iostream>
#include <vector>
#define int long long
using namespace std;
typedef pair<int, int> PII;
signed main()
{
cin.tie(0);
cout.tie(0);
ios::sync_with_stdio(0);
int N, L;
cin >> N >> L;
std::vector<int> A(N + 1);
for (int i = 1; i <= N; i ++)
cin >> A[i];
int Result = 0;
for (int i = 1; i <= N; i ++)
if (A[i] >= L)
Result ++;
cout << Result << endl;
return 0;
}
B - Minimize Abs 1
Description
Problem Statement
You are given an integer sequence
A
=
(
A
1
,
A
2
,
…
,
A
N
)
A=(A_1,A_2,\ldots,A_N)
A=(A1,A2,…,AN) of length
N
N
N and integers
L
L
L and
R
R
R such that
L
≤
R
L\leq R
L≤R.
For each
i
=
1
,
2
,
…
,
N
i=1,2,\ldots,N
i=1,2,…,N, find the integer
X
i
X_i
Xi that satisfies both of the following conditions. Note that the integer to be found is always uniquely determined.
L
≤
X
i
≤
R
L\leq X_i \leq R
L≤Xi≤R.
For every integer
Y
Y
Y such that
L
≤
Y
≤
R
L \leq Y \leq R
L≤Y≤R, it holds that
∣
X
i
−
A
i
∣
≤
∣
Y
−
A
i
∣
|X_i - A_i| \leq |Y - A_i|
∣Xi−Ai∣≤∣Y−Ai∣.
Constraints
1
≤
N
≤
2
×
1
0
5
1\leq N\leq 2\times 10^5
1≤N≤2×105
1
≤
L
≤
R
≤
1
0
9
1\leq L\leq R \leq 10^9
1≤L≤R≤109
1
≤
A
i
≤
1
0
9
1\leq A_i\leq 10^9
1≤Ai≤109
All input values are integers.
Input
The input is given from Standard Input in the following format:
N N N L L L R R R
A 1 A_1 A1 … \ldots … A N A_N AN
Output
Print X i X_i Xi for i = 1 , 2 , … , N i=1,2,\ldots,N i=1,2,…,N, separated by spaces.
Sample Input 1
5 4 7
3 1 4 9 7
Sample Output 1
4 4 4 7 7
For
i
=
1
i=1
i=1:
∣
4
−
3
∣
=
1
|4-3|=1
∣4−3∣=1
∣
5
−
3
∣
=
2
|5-3|=2
∣5−3∣=2
∣
6
−
3
∣
=
3
|6-3|=3
∣6−3∣=3
∣
7
−
3
∣
=
4
|7-3|=4
∣7−3∣=4
Thus,
X
i
=
4
X_i = 4
Xi=4.
Sample Input 2
3 10 10
11 10 9
Sample Output 2
10 10 10
Solution
涉及算法:贪心
通过贪心的思想,分为 3 3 3 中情况:
- A i ∈ [ L , R ] A_i \in [L,R] Ai∈[L,R]:答案为 A i A_i Ai
- A i < L A_i < L Ai<L:答案为 L L L
- A i > R A_i>R Ai>R:答案为 R R R
Code
#include <iostream>
#define int long long
using namespace std;
typedef pair<int, int> PII;
const int SIZE = 2e5 + 10;
int N, L, R;
int A[SIZE];
signed main()
{
cin.tie(0);
cout.tie(0);
ios::sync_with_stdio(0);
cin >> N >> L >> R;
for (int i = 1; i <= N; i ++)
cin >> A[i];
for (int i = 1; i <= N; i ++)
if (A[i] >= L && A[i] <= R)
cout << A[i] << " ";
else if (L > A[i])
cout << L << " ";
else
cout << R << " ";
return 0;
}
C - Minimize Abs 2
Description
Problem Statement
You are given a positive integer
D
D
D.
Find the minimum value of
∣
x
2
+
y
2
−
D
∣
|x^2+y^2-D|
∣x2+y2−D∣ for non-negative integers
x
x
x and
y
y
y.
Constraints
1
≤
D
≤
2
×
1
0
12
1\leq D \leq 2\times 10^{12}
1≤D≤2×1012
All input values are integers.
Input
The input is given from Standard Input in the following format:
D D D
Output
Print the answer.
Sample Input 1
21
Sample Output 1
1
For
x
=
4
x=4
x=4 and
y
=
2
y=2
y=2, we have
∣
x
2
+
y
2
−
D
∣
=
∣
16
+
4
−
21
∣
=
1
|x^2+y^2-D| = |16+4-21|=1
∣x2+y2−D∣=∣16+4−21∣=1.
There are no non-negative integers
x
x
x and
y
y
y such that
∣
x
2
+
y
2
−
D
∣
=
0
|x^2+y^2-D|=0
∣x2+y2−D∣=0, so the answer is
1
1
1.
Sample Input 2
998244353
Sample Output 2
0
Sample Input 3
264428617
Sample Output 3
32
Solution
涉及算法:数学,枚举
通过枚举 x x x,随之 y y y 也可以确定。
因为 ∣ x 2 + y 2 − D ∣ |x^2+y^2-D| ∣x2+y2−D∣ 最小,即 x 2 + y 2 x^2+y^2 x2+y2 最接近 D D D。
所以, y = D − x 2 y=\sqrt{D-x^2} y=D−x2,但是为了防止一些精度等问题,作者采取了上下浮动 1 1 1 取最小值。即 y − 1 y-1 y−1, y + 1 y+1 y+1, y y y 都算出值并取出最小值。
Code
#include <iostream>
#include <cmath>
#define int long long
using namespace std;
typedef pair<int, int> PII;
int D;
int Calc(int x, int y)
{
return abs(x * x + y * y - D);
}
signed main()
{
cin.tie(0);
cout.tie(0);
ios::sync_with_stdio(0);
cin >> D;
int N = sqrtl(D) + 1, Result = 1e18;
for (int x = 0; x <= N; x ++)
{
int y = sqrtl(abs(D - x * x)), V = min(Calc(x, y), min(Calc(x, y - 1), Calc(x, y + 1)));
Result = min(Result, V);
}
cout << Result << endl;
return 0;
}
D - Counting Ls
Description
Problem Statement
You are given an
N
×
N
N \times N
N×N grid. Let
(
i
,
j
)
(i,j)
(i,j) denote the cell in the
i
i
i-th row from the top and the
j
j
j-th column from the left.
The states of the cells are given by
N
N
N strings of length
N
N
N,
S
1
,
S
2
,
…
,
S
N
S_1, S_2, \dots, S_N
S1,S2,…,SN, in the following format:
If the
j
j
j-th character of
S
i
S_i
Si is o, there is an o written in cell
(
i
,
j
)
(i,j)
(i,j).
If the
j
j
j-th character of
S
i
S_i
Si is x, there is an x written in cell
(
i
,
j
)
(i,j)
(i,j).
Find the number of triples of cells that satisfy all of the following conditions:
The three cells in the triple are distinct.
All three cells have an o written in them.
Exactly two of the cells are in the same row.
Exactly two of the cells are in the same column.
Here, two triples are considered different if and only if some cell is contained in exactly one of the triples.
Constraints
N
N
N is an integer between
2
2
2 and
2000
2000
2000, inclusive.
S
i
S_i
Si is a string of length
N
N
N consisting of o and x.
Input
The input is given from Standard Input in the following format:
N N N
S 1 S_1 S1
S 2 S_2 S2
⋮ \vdots ⋮
S N S_N SN
Output
Print the answer as an integer.
Sample Input 1
3
ooo
oxx
xxo
Sample Output 1
4
The following four triples satisfy the conditions:
(
1
,
1
)
,
(
1
,
2
)
,
(
2
,
1
)
(1,1),(1,2),(2,1)
(1,1),(1,2),(2,1)
(
1
,
1
)
,
(
1
,
3
)
,
(
2
,
1
)
(1,1),(1,3),(2,1)
(1,1),(1,3),(2,1)
(
1
,
1
)
,
(
1
,
3
)
,
(
3
,
3
)
(1,1),(1,3),(3,3)
(1,1),(1,3),(3,3)
(
1
,
2
)
,
(
1
,
3
)
,
(
3
,
3
)
(1,2),(1,3),(3,3)
(1,2),(1,3),(3,3)
Sample Input 2
4
oxxx
xoxx
xxox
xxxo
Sample Output 2
0
Sample Input 3
15
xooxxooooxxxoox
oxxoxoxxxoxoxxo
oxxoxoxxxoxoxxx
ooooxooooxxoxxx
oxxoxoxxxoxoxxx
oxxoxoxxxoxoxxo
oxxoxooooxxxoox
xxxxxxxxxxxxxxx
xooxxxooxxxooox
oxxoxoxxoxoxxxo
xxxoxxxxoxoxxoo
xooxxxooxxoxoxo
xxxoxxxxoxooxxo
oxxoxoxxoxoxxxo
xooxxxooxxxooox
Sample Output 3
2960
Solution
涉及算法:前缀和 & 差分,排列组合
其实用不到这么多算法,只是作者做麻烦了(qwq
这道题其实就是找 L 形,所以可以枚举拐点。
那么对于每一个拐点,有多少个 L 行呢?
设正上方 o 的个数为
u
u
u,左方 o 的个数为
l
l
l,右方 o 的个数为
r
r
r,下方 o 的个数为
d
d
d
则,个数为 u ⋅ l + u ⋅ r + d ⋅ l + d ⋅ r u\cdot l + u\cdot r + d\cdot l + d\cdot r u⋅l+u⋅r+d⋅l+d⋅r,即 ( u + d ) ⋅ ( l + r ) (u+d)\cdot (l+r) (u+d)⋅(l+r)
解释:就是每一个上边的 o 都可以和左边,右边任意一个 o 相结合,形成 L 形。下边的同理。
Code
#include <iostream>
#define int long long
using namespace std;
typedef pair<int, int> PII;
const int SIZE = 2e3 + 10;
int N;
int Line[SIZE][SIZE], Col[SIZE][SIZE];
char Map[SIZE][SIZE];
signed main()
{
cin.tie(0);
cout.tie(0);
ios::sync_with_stdio(0);
cin >> N;
for (int i = 1; i <= N; i ++)
for (int j = 1; j <= N; j ++)
{
cin >> Map[i][j];
Line[i][j] = Line[i][j - 1] + (Map[i][j] == 'o');
Col[i][j] = Col[i - 1][j] + (Map[i][j] == 'o');
}
int Result = 0;
for (int i = 1; i <= N; i ++)
for (int j = 1; j <= N; j ++)
{
if (Map[i][j] == 'x') continue;
int Up = Col[i - 1][j], Down = Col[N][j] - Col[i][j], Left = Line[i][j - 1], Right = Line[i][N] - Line[i][j];
Result += Up * (Right + Left) + Down * (Right + Left);
}
cout << Result << endl;
return 0;
}
E - Mex and Update
Description
Problem Statement
You are given a sequence
A
=
(
A
1
,
A
2
,
…
,
A
N
)
A=(A_1,A_2,\dots,A_N)
A=(A1,A2,…,AN) of length
N
N
N.
Respond to the following
Q
Q
Q queries in the order they are given.
The
k
k
k-th query is given in the following format:
i k i_k ik x k x_k xk
First, change
A
i
k
A_{i_k}
Aik to
x
k
x_k
xk. This change will carry over to subsequent queries.
Then, print the
m
e
x
\rm{mex}
mex of
A
A
A.
The
m
e
x
\rm{mex}
mex of
A
A
A is the smallest non-negative integer not contained in
A
A
A.
Constraints
All input values are integers.
1
≤
N
,
Q
≤
2
×
1
0
5
1 \le N,Q \le 2 \times 10^5
1≤N,Q≤2×105
0
≤
A
i
≤
1
0
9
0 \le A_i \le 10^9
0≤Ai≤109
1
≤
i
k
≤
N
1 \le i_k \le N
1≤ik≤N
0
≤
x
k
≤
1
0
9
0 \le x_k \le 10^9
0≤xk≤109
Input
Input is given from Standard Input in the following format:
N N N Q Q Q
A 1 A_1 A1 A 2 A_2 A2 … \dots … A N A_N AN
i 1 i_1 i1 x 1 x_1 x1
i 2 i_2 i2 x 2 x_2 x2
⋮ \vdots ⋮
i Q i_Q iQ x Q x_Q xQ
Output
Print
Q
Q
Q lines in total.
The
k
k
k-th line should contain the answer to the
k
k
k-th query as an integer.
Sample Input 1
8 5
2 0 2 2 1 1 2 5
4 3
4 4
6 3
8 1000000000
2 1
Sample Output 1
4
3
6
5
0
Initially, the sequence
A
A
A is
(
2
,
0
,
2
,
2
,
1
,
1
,
2
,
5
)
(2,0,2,2,1,1,2,5)
(2,0,2,2,1,1,2,5).
This input gives you five queries.
The first query changes
A
4
A_4
A4 to
3
3
3, making
A
=
(
2
,
0
,
2
,
3
,
1
,
1
,
2
,
5
)
A=(2,0,2,3,1,1,2,5)
A=(2,0,2,3,1,1,2,5).
At this point, the
m
e
x
\rm{mex}
mex of
A
A
A is
4
4
4.
The second query changes
A
4
A_4
A4 to
4
4
4, making
A
=
(
2
,
0
,
2
,
4
,
1
,
1
,
2
,
5
)
A=(2,0,2,4,1,1,2,5)
A=(2,0,2,4,1,1,2,5).
At this point, the
m
e
x
\rm{mex}
mex of
A
A
A is
3
3
3.
The third query changes
A
6
A_6
A6 to
3
3
3, making
A
=
(
2
,
0
,
2
,
4
,
1
,
3
,
2
,
5
)
A=(2,0,2,4,1,3,2,5)
A=(2,0,2,4,1,3,2,5).
At this point, the
m
e
x
\rm{mex}
mex of
A
A
A is
6
6
6.
The fourth query changes
A
8
A_8
A8 to
1000000000
1000000000
1000000000, making
A
=
(
2
,
0
,
2
,
4
,
1
,
3
,
2
,
1000000000
)
A=(2,0,2,4,1,3,2,1000000000)
A=(2,0,2,4,1,3,2,1000000000).
At this point, the
m
e
x
\rm{mex}
mex of
A
A
A is
5
5
5.
The fifth query changes
A
2
A_2
A2 to
1
1
1, making
A
=
(
2
,
1
,
2
,
4
,
1
,
3
,
2
,
1000000000
)
A=(2,1,2,4,1,3,2,1000000000)
A=(2,1,2,4,1,3,2,1000000000).
At this point, the
m
e
x
\rm{mex}
mex of
A
A
A is
0
0
0.
Solution
涉及算法:权值线段树,二分
大家可能会问了:这题不是 set 吗?怎么成线段树了?
不要问,问就是血的教训
比赛时,看见修改直接想线段树,白写了 103 103 103 行(虽然没压行)
这里将讲解一下比赛时的做法,如果大家想练数据结构的话,可以来看一看。
首先,如果这个数的权值大于 N N N,我们不需要进行任何操作,因为对于 m e x \mathrm{mex} mex 没有任何作用。
证明:最多只有 N N N 个数,如果这 N N N 个数为 0 ∼ N − 1 0\sim N-1 0∼N−1,也最多输出 N N N,所以大于 N N N 的数是完全没有作用的,也就是说他以及他之前的数不可能都有。
对于每一个操作,如果权值小于等于 N N N,我们在新权值的位置加 1 1 1,旧权值的位置减 1 1 1。
对于查询,二分,对于每一个点判断 0 ∼ m i d 0\sim mid 0∼mid,线段树中有数位置的和,如果等于 m i d + 1 mid+1 mid+1,则说明 0 ∼ m i d 0\sim mid 0∼mid 全部都有值,左端点拨到 m i d mid mid,反之右端点拨到 m i d − 1 mid-1 mid−1。
所以,线段树应该存储两个信息:
- 该权值出现的次数
- 该区间有值的数的个数和
具体详情见代码(码风自我感觉良好
Code
#include <iostream>
#include <unordered_map>
#define int long long
using namespace std;
typedef pair<int, int> PII;
const int SIZE = 2e5 + 10;
int N, Q;
int A[SIZE];
unordered_map<int, int> Has;
struct Segment
{
int l, r;
int Sum, Count;
}Tree[SIZE * 4];
void Pushup(int u)
{
Tree[u].Sum = Tree[u << 1].Sum + Tree[u << 1 | 1].Sum;
Tree[u].Count = Tree[u << 1].Count + Tree[u << 1 | 1].Count;
}
void Build(int u, int l, int r)
{
if (l == r)
{
Tree[u] = {l, l, Has[l], min(1ll, Has[l])};
return;
}
Tree[u] = {l, r};
int mid = l + r >> 1;
Build(u << 1, l, mid), Build(u << 1 | 1, mid + 1, r);
Pushup(u);
}
void Modify(int u, int x, int d)
{
if (Tree[u].l == Tree[u].r && Tree[u].l == x)
{
Tree[u].Sum += d;
Tree[u].Count = (Tree[u].Sum >= 1);
return;
}
int mid = Tree[u].l + Tree[u].r >> 1;
if (mid >= x) Modify(u << 1, x, d);
else Modify(u << 1 | 1, x, d);
Pushup(u);
}
int Query(int u, int l, int r)
{
if (Tree[u].l >= l && Tree[u].r <= r)
return Tree[u].Count;
int mid = Tree[u].l + Tree[u].r >> 1, Result = 0;
if (mid >= l) Result += Query(u << 1, l, r);
if (mid < r) Result += Query(u << 1 | 1, l, r);
return Result;
}
signed main()
{
cin.tie(0);
cout.tie(0);
ios::sync_with_stdio(0);
cin >> N >> Q;
for (int i = 1; i <= N; i ++)
cin >> A[i], Has[A[i]] ++;
Build(1, 0, N);
while (Q --)
{
int I, X;
cin >> I >> X;
if (A[I] <= N) Modify(1, A[I], -1);
if (X <= N) Modify(1, X, 1);
A[I] = X;
int l = 0, r = N + 1, Result = 0;
while (l < r)
{
int mid = l + r + 1 >> 1;
if (Query(1, 0, mid) == mid + 1) l = mid, Result = max(Result, mid + 1);
else r = mid - 1;
}
if (Query(1, 0, 0) == 1) Result = max(1ll, Result);
cout << Result << endl;
}
return 0;
}
F - Minimize Bounding Square
Description
Problem Statement
There are
N
N
N points labeled
1
,
2
,
…
,
N
1, 2, \dots, N
1,2,…,N on the
x
y
xy
xy-plane. Point
i
i
i is located at coordinates
(
X
i
,
Y
i
)
(X_i, Y_i)
(Xi,Yi).
You can perform the following operation between
0
0
0 and
K
K
K times, inclusive.
First, choose one of the
N
N
N points. Let
k
k
k be the selected point, and assume it is currently at
(
x
,
y
)
(x, y)
(x,y).
Next, choose and execute one of the following four actions:
Move point
k
k
k along the
x
x
x-axis by
+
1
+1
+1. The coordinates of point
k
k
k become
(
x
+
1
,
y
)
(x+1, y)
(x+1,y).
Move point
k
k
k along the
x
x
x-axis by
−
1
-1
−1. The coordinates of point
k
k
k become
(
x
−
1
,
y
)
(x-1, y)
(x−1,y).
Move point
k
k
k along the
y
y
y-axis by
+
1
+1
+1. The coordinates of point
k
k
k become
(
x
,
y
+
1
)
(x, y+1)
(x,y+1).
Move point
k
k
k along the
y
y
y-axis by
−
1
-1
−1. The coordinates of point
k
k
k become
(
x
,
y
−
1
)
(x, y-1)
(x,y−1).
It is allowed to have multiple points at the same coordinates. Note that the input may already have multiple points at the same coordinates.
After all your operations, draw one square that includes all the
N
N
N points inside or on the circumference, with each side parallel to the
x
x
x- or
y
y
y-axis.
Find the minimum possible value for the length of a side of this square. This value can be shown to be an integer since all points are always on lattice points.
In particular, if all points can be made to exist at the same coordinates, the answer is considered to be
0
0
0.
Constraints
All input values are integers.
1
≤
N
≤
2
×
1
0
5
1 \le N \le 2 \times 10^5
1≤N≤2×105
0
≤
K
≤
4
×
1
0
14
0 \le K \le 4 \times 10^{14}
0≤K≤4×1014
0
≤
X
i
,
Y
i
≤
1
0
9
0 \le X_i, Y_i \le 10^9
0≤Xi,Yi≤109
Input
Input is given from Standard Input in the following format:
$N$ $K$
$X_1$ $Y_1$
$X_2$ $Y_2$
$\vdots$
$X_N$ $Y_N$
Output
Print the answer as an integer.
Sample Input 1
6 5
2 0
5 2
0 3
3 2
3 4
1 5
Sample Output 1
3
The figure below illustrates this case with the horizontal
x
x
x-axis and the vertical
y
y
y-axis.
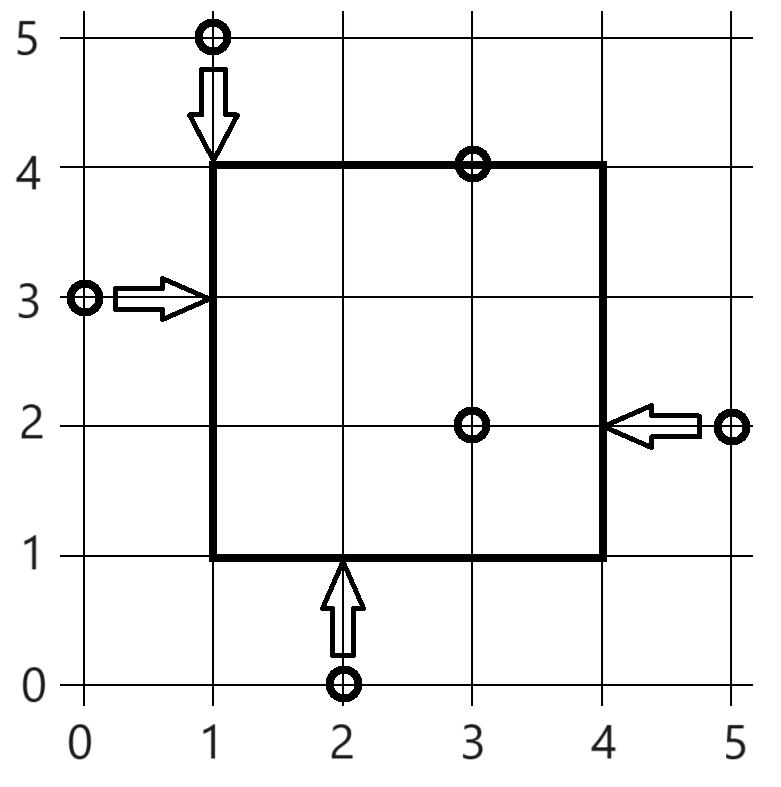
For example, after performing four moves following the arrows in the figure, you can include all points inside or on the circumference of the square shown in the figure with a side length of
3
3
3, and this can be shown to be the minimum value.
Sample Input 2
4 400000000000000
1000000000 1000000000
1000000000 1000000000
1000000000 1000000000
1000000000 1000000000
Sample Output 2
0
All points already exist at the same coordinates from the beginning.
For example, by performing zero operations, all points can be made to exist at the same coordinates, so the answer for this input is
0
0
0.
Sample Input 3
10 998244353
489733278 189351894
861289363 30208889
450668761 133103889
306319121 739571083
409648209 922270934
930832199 304946211
358683490 923133355
369972904 539399938
915030547 735320146
386219602 277971612
Sample Output 3
484373824
Solution
涉及算法:二分
本题的精华是将 x x x 轴, y y y 轴,分开来计算,即 x x x 轴上选出一个区间, y y y 轴上选出一个长度相等的区间。
我们可以二分出正方形的边长,那么只需要枚举左端点即可,这样可推出右端点。
如何计算所有点进入该区间的操作次数呢?
在左端点左边的点的步数为左端点减去左边的点的坐标,在右端点右边的点的步数为右边的点减去右端点。
Code
#include <iostream>
#include <vector>
#include <algorithm>
#define int long long
using namespace std;
typedef pair<int, int> PII;
const int SIZE = 2e5 + 10;
int N, K;
int X[SIZE], Y[SIZE], Sum[SIZE];
int Calc(int A[], int S)
{
std::vector<int> B;
for (int i = 1; i <= N; i ++)
B.push_back(A[i]), B.push_back(A[i] - S);
for (int i = 1; i <= N; i ++)
Sum[i] = Sum[i - 1] + A[i];
int Result = 1e18;
for (auto c : B)
{
int L = c, R = c + S;
int Left = lower_bound(A + 1, A + 1 + N, L) - A - 1;
int Right = upper_bound(A + 1, A + 1 + N, R) - A;
int CA = 0, CB = 0;
if (Left > 0)
CA += L * Left - Sum[Left];
if (Right <= N)
CB += Sum[N] - Sum[Right - 1] - R * (N - Right + 1);
Result = min(Result, CA + CB);
}
return Result;
}
signed main()
{
cin.tie(0);
cout.tie(0);
ios::sync_with_stdio(0);
cin >> N >> K;
for (int i = 1; i <= N; i ++)
cin >> X[i] >> Y[i];
sort(X + 1, X + 1 + N);
sort(Y + 1, Y + 1 + N);
int l = 0, r = 2e9;
while (l < r)
{
int mid = l + r >> 1;
if (Calc(X, mid) + Calc(Y, mid) <= K)
r = mid;
else
l = mid + 1;
}
cout << r << endl;
return 0;
}